浅谈费米能级

定义：在绝对0K的条件下，自由电子所处的最高能级，常用Ef表示。它是一个理想化的绝对条件。

先来解释一下能级能带的概念吧。由量子力学最基本的假设可知，能级不具备连续性。（以H原子为例）

当体系中有很多原子时，原子间存在相互作用，导致能级移动，原本一条的能级扩展成了一组差别很小的结构，我们称之为能带/允带。

由于能带是从能级扩展而出的概念，不同能级的能带间存在没有能级的间隔，这个间隔就是禁带，电子无法取到禁带中的能量。

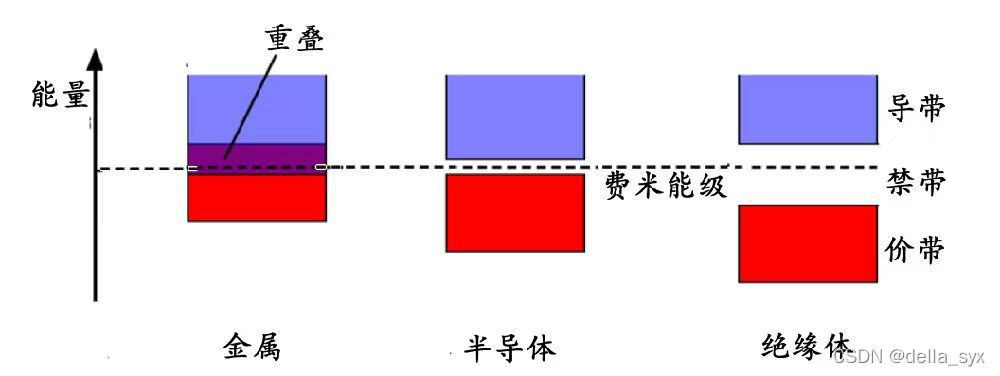
基态原子电子填充是从最低能级开始依次往高能级向上填充的过程。对于半导体，电子刚好填充到某一个能带满了，下一个能带全空，这些被填满的能带称为满带，满带中能量最高的一条称为价带。我们可以认为价带中的电子是不导电的。

对于半导体，能量最高的一个价带到能量更高的下一个能带之间有一个禁带，但是这个禁带的宽度不是很大，所以有一些电子有机会跃迁到下一个能带。由于这个能带几乎是空的，所以电子跃迁到这个能级之后就可以自由奔跑，这个能带就是导带。

ps：对于绝缘体，这个禁带宽度太大，基本不可能有电子跃迁过去；对于金属，则不存在禁带，导带与价带直接重合了，不需要跃迁就可以导电。

半导体中的载流子有带负电的自由电荷以及带正电的自由空穴。上述粒子均为自由电子。

引入费米能级的概念是为了方便描述电子在能带中的分布。

半导体在绝对0度的条件下（理想条件），费米能级以下的所有能级都被电子填满，费米能级以上的所有能级都是空的。当温度高于绝对0度时，可以通过费米能级和温度来计算电子的费米-狄拉克分布。

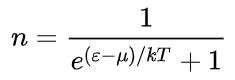，n为粒子占据概率，ε为能量，μ为化学势即费米能级，T为温度。

 （费米-狄拉克分布）

根据公式，我们发现，当ε=μ时，n=1/2，即无论T是否为绝对零度，费米能级均满足n=1/2的性质，所以我们可以由粒子出现概率是否为50%判断粒子是否在费米能级上。

而在半导体中，由于禁带的存在，绝对零度下电子填充的最高能级其实是价带顶，而本征半导体的费米面认为是在禁带中央，这是因为采用了电子出现概率为50%的定义，其费米面刚好就在中央。

纯净的半导体（本征半导体）的导电能力很差，为了使更多的载流子跃迁到导带，需要高温，或对半导体进行掺杂，通过掺杂来引入新的能级。