宏观经济学 索洛模型

索洛增长模型，又称新古典经济增长模型、外生经济增长模型，是在新古典经济学框架内所提出的著名的经济增长模型。
主要用于解释固定资本增加，对GDP 所产生的影响。
该模型假设投资的边际收益率递减，即在一定数量后生产得越多，效率越低。
模型结论：经济增长的路径是稳定的。在长期只有技术进步是增长的来源。

第八章

前提

假设1：生产函数规模报酬不变，即：$zY=F(zK,zL)$
注意：规模报酬不变，不是边际收益不变

生产函数除以人数L，则得到：
$Y/L=F(K/L,1)$

即，人均产出仅与人均资本（存量）相关

定义：
$y=Y/L$
$k=K/L$

生产函数表示为：$y=f(k)=F(K/L,1)$

平衡的增长，在达到稳态后持续稳定增长
水平的增长，是在达到稳态前的短暂增长，在达到稳态后维持水平不再增长

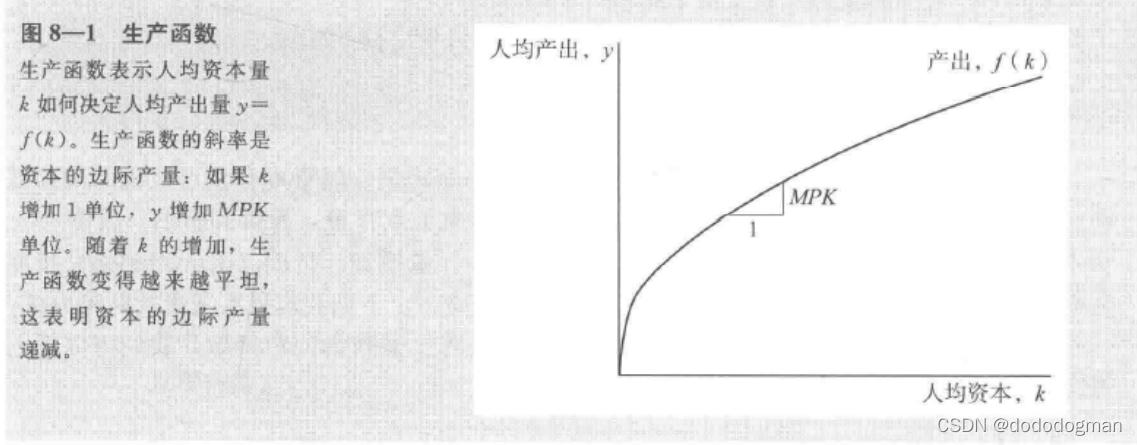
生产函数

名词解释：在一定时期内，在技术水平不变的情况下，生产中所用的各种生产要素的数量与所能生产的最大产量之间的关系

最常见的生产函数：柯布-道格拉斯生产函数（貌似不考）

$Y=F(K,\bar{L})=A{K}^{\alpha }{L}^{\beta }$

α+β＞1，则规模报酬递增；

α+β = 1，则规模报酬不变；

α+β＜1，则规模报酬递减。

Y代表GDP收入，A代表效率，K代表资本（资本存量），L代表生产人数；
$\alpha ,\beta$分别代表资本和劳动的产出份额（或产出弹性）

消费函数

人均： y = c