机械臂轨迹规划方法综述

唐豆豆*

已于 2025-03-17 16:01:06 修改

阅读量2.8k

点赞数 32

分类专栏：双臂机器人项目文章标签： python 轨迹规划插值算法

于 2025-03-06 21:12:18 首次发布

本文链接：https://blog.csdn.net/doudou2weiwei/article/details/145995511

版权

双臂机器人项目专栏收录该内容

8 篇文章

订阅专栏

更新：2025.3.17，补充了关节轨迹规划部分（点到点五次多项式插值）

一、机械臂轨迹规划概述

机械臂的运动规划包括路径规划和轨迹规划两个方面。

1.路径规划：

定义：路径规划是指在给定的起点和终点之间，寻找一条无碰撞的路径。路径可以是直线、曲线或者其他形状，主要关注的是路径的几何形状。

目标：避障、路径尽可能短、平滑

常用方法：直线插补、圆弧插补、B样条、多项式插值、RRT、基于图搜索的方法、人工势场法等

2.轨迹规划

定义：轨迹规划是在路径规划的基础上，为路径赋予时间信息，包括速度、加速度等，是的机械臂能够按照预定的时间和运动特性完成运动

目标：时间优化、能量优化、运动平滑、动态约束

常用方法：笛卡尔轨迹规划（对末端执行器位姿有严格要求的场合）、关节空间轨迹规划（对关节运动由严格要求的场合）

关节空间轨迹规划：将关节变量表示成时间的函数，并规划它的一阶和二阶导数。

二、插补与拟合

1.直线插补

1）本质上就是在起始位置和目标位置之间生成一段直线轨迹。

2）其求解思路如下：

确定起始位置==》确定单位步长（dx，dy，dz），也就是（终点坐标-起点坐标）/（插值点个数-1）==》确定插值点坐标，其计算公式如下

def linear_interpolation_3d(start_point, end_point, num_points):
    """
    生成从start_point到end_point的三维直线插补点。
    参数:
    start_point (tuple): 起始点坐标，格式为(x, y, z)。
    end_point (tuple): 终止点坐标，格式为(x, y, z)。
    num_points (int): 要生成的插补点数量，包括起始点和终止点。
    返回:
    list: 包含插补点坐标的列表。
    """
    points = []
    x_start, y_start, z_start = start_point
    x_end, y_end, z_end = end_point
    
    # 计算x、y和z方向上的增量
    dx = (x_end - x_start) / (num_points - 1)
    dy = (y_end - y_start) / (num_points - 1)
    dz = (z_end - z_start) / (num_points - 1)
    # 生成插补点, 这里的dx，dy，dz就是单位步长，也就是每个插补点之间的间距是恒定的
    for i in range(num_points):
        x = x_start + i * dx
        y = y_start + i * dy
        z = z_start + i * dz
        points.append((x, y, z))
    return points

# 使用示例
start_point = (0, 0, 0)  # 起始点坐标
end_point = (10, 10, 10)  # 终止点坐标
num_points = 5  # 生成5个插补点，包括起始点和终止点

interpolated_points = linear_interpolation_3d(start_point, end_point, num_points)
print(interpolated_points)

2.圆弧插补

1）圆弧插补可以用于生成起点和终点之间的一段圆弧路径。

2）其求解思路如下：

给定起点、终点、圆心坐标==》计算起点与终点间对应圆弧的夹角，其计算公式如下：

==》计算单位步长（角度）==》计算插值点位置

import numpy as np

def circular_interpolation_3d_with_z(start_point, end_point, center_point, num_points):
    """
    生成从start_point到end_point的三维圆弧插补点，同时考虑Z坐标的线性变化。
    参数:
    start_point (tuple): 起始点坐标，格式为(x, y, z)。
    end_point (tuple): 终止点坐标，格式为(x, y, z)。
    center_point (tuple): 圆心点坐标，格式为(x, y, z)。
    num_points (int): 要生成的插补点数量，包括起始点和终止点。
    返回:
    list: 包含插补点坐标的列表。
    """
    points = []
    x_start, y_start, z_start = start_point
    x_end, y_end, z_end = end_point
    x_center, y_center, z_center = center_point
    # 计算从圆心到起点和终点的向量
    vector_start = np.array([x_start - x_center, y_start - y_center])
    vector_end = np.array([x_end - x_center, y_end - y_center])
    # 计算圆弧的角度
    angle = np.arccos(np.dot(vector_start, vector_end) / (np.linalg.norm(vector_start) * np.linalg.norm(vector_end)))
    # 计算插补点的步长
    angle_step = angle / (num_points - 1)
    # 生成插补点，Z采用直线插补，x，y采用圆弧插补
    for i in range(num_points):
        t = i * angle_step
        point = (center_point[0] + np.cos(t) * np.linalg.norm(vector_start),
                 center_point[1] + np.sin(t) * np.linalg.norm(vector_start),
                 z_start + i * (z_end - z_start) / (num_points - 1))
        points.append(point)
    return points

# 使用示例
start_point = (0, 0, 0)  # 起始点坐标
end_point = (10, 0, 5)  # 终止点坐标
center_point = (5, 0, 2.5)  # 圆心点坐标
num_points = 100  # 生成100个插补点，包括起始点和终止点

interpolated_points = circular_interpolation_3d_with_z(start_point, end_point, center_point, num_points)

# 输出插补点
for point in interpolated_points:
    print(point)

3. Bezier曲线

学习参考资料：贝塞尔(Bezier)曲线与B样条_哔哩哔哩_bilibili

1）贝塞尔曲线是通过一组控制点来定义曲线的形状，这些控制点不仅决定了曲线的起点和终点，还影响曲线的弯曲程度和方向。假设一共有n+1个控制点，就可以确定n次的贝塞尔曲线：

（公式1）

这个式子解开后就是：

其中W表示基，P为控制点坐标

计算W的代码如下：

W = comb(n, i) * (t ** i) * ((1 - t) ** (n - i)) # 形状会与t的一致

2）下面这个图共有3个点，可以确定一个2次的贝塞尔曲线，图中可以看出，t属于[0,1], 用贝塞尔曲线公式（1）表达就是：

以下分别是1次，2次，3次，4次贝塞尔曲线，从图中可以看出贝塞尔曲线的递推关系

3)具体形成Bezier曲线的代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb

def bezier_curve(points, num_points=100):
    """
    计算任意阶数的贝塞尔曲线。
    :param points: 控制点列表，格式为 [(x1, y1), (x2, y2), ..., (xn, yn)]
    :param num_points: 要生成的曲线点的数量
    :return: 一个包含曲线点的数组
    """
    n = len(points) - 1  # 贝塞尔曲线的阶数
    t = np.linspace(0, 1, num_points)  # 参数t从0到1,等间距
    curve_points = np.zeros((num_points, 2))  # 初始化曲线点数组

    # 遍历每个控制点，计算贝塞尔曲线的每个点
    for i in range(len(points)):
        # 计算基函数，comb（n,i）表示的是C(N,I),这个bernstein参数对应的是基函数
        W = comb(n, i) * (t ** i) * ((1 - t) ** (n - i)) # 形状会与t的一致
        curve_points[:, 0] += W * points[i][0]  # x坐标
        curve_points[:, 1] += W * points[i][1]  # y坐标

    return curve_points # 返回值为bezier曲线上的点

# 示例：定义一组控制点（可以是任意阶数）
# control_points = [(0, 0), (1, 3), (3, -1), (4, 2), (5, 4)]  # 4阶贝塞尔曲线

control_points = [(0, 0), (1, 3), (3, -1), (4, 2), (5, 4), (6, 7)]  # 5阶贝塞尔曲线

# 计算贝塞尔曲线
curve_points = bezier_curve(control_points, num_points=100)

# 绘制贝塞尔曲线
plt.figure(figsize=(6, 6))
plt.plot(curve_points[:, 0], curve_points[:, 1], label="Bezier Curve", color="blue")

# 绘制控制点和控制多边形
control_x, control_y = zip(*control_points)
plt.plot(control_x, control_y, "o--", label="Control Points", color="red")

# 添加图例和标题
plt.legend()
plt.title("General Bezier Curve")
plt.xlabel("X")
plt.ylabel("Y")
plt.grid(True)
plt.axis("equal")
plt.show()

4.B样条曲线

学习参考资料：贝塞尔(Bezier)曲线与B样条_哔哩哔哩_bilibili

8.5.2 B样条曲线定义（1）_哔哩哔哩_bilibili

1）和Bezier样条一样，B样条也是通过逼近一组控制点来产生的。但是B样条具有两个Bezier样条所不具备的特点：B样条多项式的次数可独立于控制点数目（有一定限制）；B样条允许局部控制曲线或曲面。

2）B样条的相关概念：

控制点：通过控制点可以控制曲线形状，假设有n+1个控制点P0，P1，。。。Pn

节点：认为将目标曲线分为若干个部分，比如m+1个节点t0,t1,...tm，它们可以将曲线划分为m段

次：对于k阶，就是k-1次多项式

3）k次B样条曲线计算方法

B样条曲线的数学表达式如下：

•Pi ：控制多边形的顶点

•K : 多项式的阶数， K 阶， K-1 次

•

：K阶 B 样条基函数

4）B样条曲线基函数的定义：

一般采用de Boor-Cox递推定义B样条基函数：即对于k阶（k-1次）B样条，构造一种递推公式，结构如下：

==>定义空间

我做了一个结构图，可以对其结构做一个说明：k阶的基函数可以由两个k-1阶的基函数组成，一个k-1阶的基函数又可以由两个k-2阶的基函数组成，依此类推。这个结构图可以说明如果要确定第i个k阶B样条基函数，需要用到ui，ui+1，.....，ui+k个节点，区间【ui，ui+k】为该基函数的支承区间（只有支承区间，基函数不为零）。

根据上述分析：

即对应ui，ui+1，。。。到ui+k。

可以得到节点空间如下：

这个时候我们会发现，这个节点空间和我们前面的B样条曲线表达式后面提供的定义空间不同，因为我们做了进一步定义空间的选取，以下图k=3，n=4为例，此时共计由8个节点，则每个基函数对应的定义空间如下，我们希望定义区间内包含所有的基函数，则选择定义区间时，我们选择从（第一个基函数）的最后一个子区间[uk-1，uk]，到（第n+1个基函数）的第一个区间[un,un+1]，也就是图里面红色框框起来的位置，通过这样的选择方式，我们能够将所有的基函数包括在定义区间里面。因此我们定义区间的选择就是[uk-1，un+1]。

5）B样条代码展示

import numpy as np
import matplotlib.pyplot as plt

# 定义二维点类
class Point2D:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def __repr__(self):
        return f"({self.x}, {self.y})"

# 定义B样条曲线类
class BSplineCurve:
    def __init__(self, control_points, degree, knot_vector=None):
        """
        初始化B样条曲线
        """
        self.control_points = control_points # 控制点坐标
        self.degree = degree # 多项式阶数
        self.num_control_points = len(control_points) # 控制点个数

        # 生成均匀节点向量
        if knot_vector is None:
            self.knot_vector = self._generate_uniform_knot_vector()

    def _generate_uniform_knot_vector(self):
        """
        生成均匀的节点向量，这里为了确保起点和终点落在曲线上做了一个设置
        """
        n = self.num_control_points - 1
        p = self.degree
        # 前面重复p+1个0，后面重复p+1个n-p+1
        # list(range(1,n-p+1))，表示生成从1开始，到n-p的整数列表
        # 以下共计n+p+1+1个节点，其中p+1是阶数
        vector = [0] * (p) + list(range(1, n + 2 -p )) +[n-p+2]*(p)
        print(vector)
        return vector

    def _basis_function(self, i, k, t):
        """
        计算B样条基函数
        :param i: 控制点索引         :param k: 次数
        :param t: 参数值             :return: 基函数值
        """
        if k == 1:
            if self.knot_vector[i] <= t <= self.knot_vector[i+1]:
                return 1.0  
            else:
                return 0.0
        else:
            # 以下公式嵌套引用_basis_function（）函数，k逐步递减，直至k=0，可以得到相应的结果
            demo1=(self.knot_vector[i+k-1] - self.knot_vector[i])
            if self.knot_vector[i+k-1] != self.knot_vector[i]:
                coef1 = (t - self.knot_vector[i]) / demo1 * self._basis_function(i, k-1, t)
            else:
                coef1=0.0
            demo2=(self.knot_vector[i+k] - self.knot_vector[i+1])
            #print(i)
            if self.knot_vector[i+k] != self.knot_vector[i+1]:
                coef2 = (self.knot_vector[i+k] - t) / demo2 * self._basis_function(i+1, k-1, t) 
            else:
                coef2=0.0
            return coef1 + coef2

    def calculate_point(self, t):
        """
        计算曲线在参数t处的点
        :param t: 参数值 t, 范围 [degress-1, num_points]
        :return: 返回曲线在 t 处的 Point2D 点
        """
        x = 0.0
        y = 0.0
        # i 从0-n
        for i in range(self.num_control_points):
            # 计算节点为t，的第i个k阶基函数的结果
            b = self._basis_function(i, self.degree, t)
            # 计算t节点对应的b样条曲线上的坐标点
            x += b * self.control_points[i].x
            y += b * self.control_points[i].y
        return Point2D(x, y)

    def generate_curve_points(self, num_points=100):
        """
        生成B样条曲线上的点
        :param num_points: 生成的曲线上点的数量    :return: 返回点列表，表示B样条曲线
        """
        curve_points = []
        # 这里的[-self.degree]就是倒着数的k个节点，也就是正着数的n+1个节点，因为总节点数是n+p+2
        for t in np.linspace(self.knot_vector[self.degree-1], self.knot_vector[-self.degree], num_points):
        #for t in np.linspace(self.knot_vector[self.degree-1], self.knot_vector[self.num_control_points], num_points):
            #print(t)
            curve_points.append(self.calculate_point(t))
        return curve_points

# 使用示例
if __name__ == "__main__":
    # 定义控制点
    control_points = [Point2D(1, 1), 
                      Point2D(2, 14), 
                      Point2D(7, 22), 
                      Point2D(9, 39),
                      Point2D(5, 49),
                      Point2D(6, 59),
                      Point2D(10,60)]

    # 创建B样条曲线对象，阶数为4，次数为3（三次B样条）
    b_spline_curve = BSplineCurve(control_points, degree=4, knot_vector=None) # 起点和终点为同一个

    # 生成并输出曲线上的点
    curve_points = b_spline_curve.generate_curve_points()

    # 绘制控制点和曲线
    control_x = [p.x for p in control_points]
    control_y = [p.y for p in control_points]
    curve_x = [p.x for p in curve_points]
    curve_y = [p.y for p in curve_points]
    #print(curve_x)

    plt.figure(figsize=(8, 5))
    plt.plot(control_x, control_y, 'ro--', label='Control Points')
    plt.plot(curve_x, curve_y, 'b-', label='B-Spline Curve')
    plt.title('B-Spline Curve')
    plt.legend()
    plt.grid()
    plt.show()

这个代码弄了好久，😄，最后发现是里面落了一个等于号，一定要仔细点，嘻嘻

2025.3.6 这几天看了这些方法，花了很多时间，先把这个分享一下，后面再补充其他算法吧！争取这一篇文章把所有的插值、规划方法弄清楚。

三、关节轨迹插值

参考教材：《机器人学》第三版，蔡自兴，谢斌编著。

1.思路

机械臂的路径点位姿已知（目标点，或路径点：X（1~n））==》运动学逆解计算（θ（1~n））==》利用插值算法对各个关节的角度轨迹进行拟合，注意:拟合时，各个路径点之间的运动时间相同。

从这里看出来，采用第二节中不同的插值方法，可以得到不同的关节轨迹函数。为了保证平滑，一般要求一阶导数和二阶导数连续可导。插值也可以采用以下方法：

2.五次多项式插值

==》以下是对于点到点规划的五次多项式插值，已知起点的关节角度和终点的关节角度，用五次多项式拟合关节变量函数。

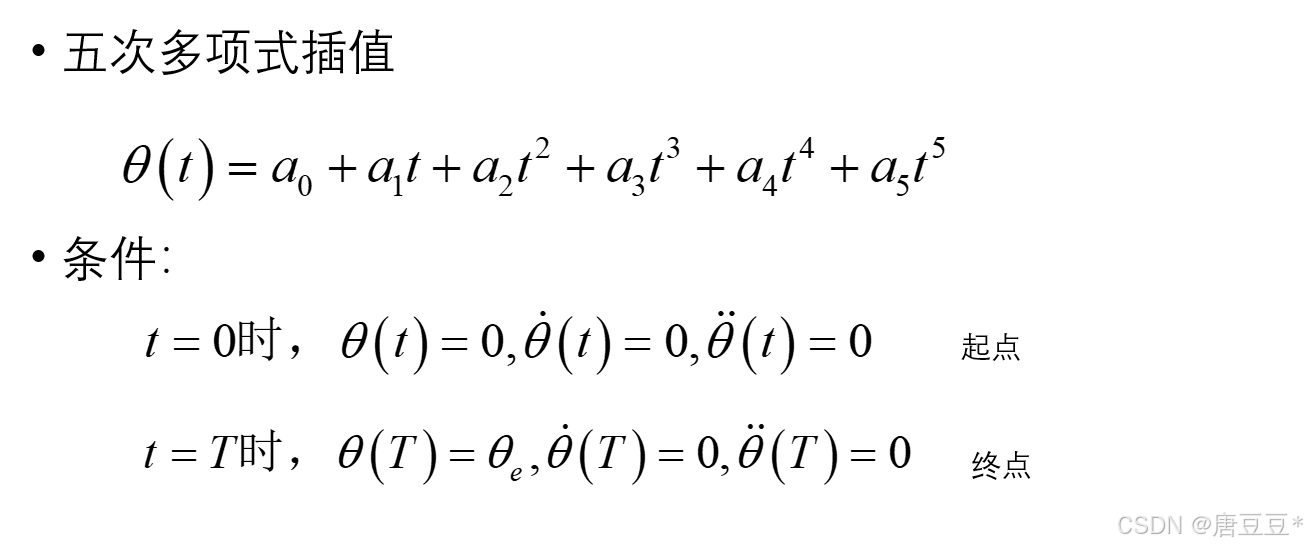
代码实现

# 本程序用于实现五次多项式插值
import numpy as np
import matplotlib.pyplot as plt

# 5次多项式规划
# q0:起始关节角，qf：终点关节角，T：总时长，dt：时间步长
def trajectory5(q0, qf, T, dt=0.01):
    # 时间向量
    t = np.arange(0, T + dt, dt)
    
    # 五次多项式系数q(t)=a0+a1*t+a2*t**2+a3*t**3+a4*t**4+a5*t**5
    a0 = q0 
    a1 = 0 
    a2 = 0  
    a3 = 10 * (qf - q0) / (T ** 3)
    a4 = -15 * (qf - q0) / (T ** 4)
    a5 = 6 * (qf - q0) / (T ** 5)
    
    # 计算关节角度
    q = a0 + a1 * t + a2 * t ** 2 + a3 * t ** 3 + a4 * t ** 4 + a5 * t ** 5
    
    return t, q

# 多关节轨迹规划
# joint_angles_initial各关节的起始角度, joint_angles_final各关节的终点角度
def plan_joint_trajectories(joint_angles_initial, joint_angles_final, T, dt=0.01):
    num_joints = len(joint_angles_initial)
    t = np.arange(0, T + dt, dt) # 对于每一个关节变量，时间序列是一致的
    q = np.zeros((len(t), num_joints))
    
    for i in range(num_joints):
        _, q[:, i] = trajectory5(joint_angles_initial[i], joint_angles_final[i], T, dt)
    
    return t, q

# 示例：6关节轨迹规划
q0 = [0, 0, 0, 0, 0, 0]  # 初始关节角度
qf = [np.pi/2, -np.pi/2, np.pi/6, np.pi/12, 0, np.pi/4]  # 目标关节角度
T = 5  # 总运动时间

t, q = plan_joint_trajectories(q0, qf, T)

# 绘制每个关节的轨迹
for i in range(len(q0)):
    plt.plot(t, q[:, i], label=f"Joint {i+1}")
plt.xlabel("Time (s)")
plt.ylabel("Joint Angle (rad)")
plt.title("Multi-Joint Trajectories")
plt.legend()
plt.grid()
plt.show()