Line Search Method 1 - 步长计算 (Step length calculation)

本文是一系列关于 Numerical Optimization 的博客的第一篇，主要讨论 Line Search Method 中步长 $\alpha$ 的计算。
该系列博客以 Nocedal 的 Numerical Optimization 一书（2006年第二版，下面简称“该书”）为主题，讨论书中的内容，并结合自己的仿真进行更生动形象的解释。博客中所有在图例中带有 “Figure” 的图片都是从Numerical Optimization 一书中截取的，在此予以说明。

在该书的前两张，作者主要对优化算法进行了入门的介绍，以及一些数学基础知识的回顾。从第三章开始将介绍主要内容，其中第三章主要介绍 Line Search Method。

Line Search Method，顾名思义，就是在某条线上去搜索下个迭代点的位置，即

$$x_{k+1}=x_k+\alpha_k p_k$$ 其中， $p_k$ 是（下降的）方向， $\alpha_k$ 是步长。这就体现出其与 Trust Region Method 的不同之处，因为后者是在当前迭代点的某个邻域内去寻找下个迭代点的值。关于 Line Search Method 中所沿的那条线，具体不同的方法有不同的选择。比如最速下降法（Steepest Descent Method）就是直接取当前点导数的反方向，即 $-\nabla f(x)$ ，而在牛顿法中的方向的选取则为 $-\nabla ^2f(x)^{-1}\nabla f(x)$ ，在拟牛顿法中则有另外的选取方法，但这些方法所选取的方向都有一个共同之处就在于要求目标函数值在当前点沿着这个方向是下降的，即
$$p_k^T\nabla f_k<0$$ 在本文接下来的内容中会主要介绍步长 $\alpha$ 的选取，也就是说，在这里我们认为方向 $p_k$ 已经确定了，然后接下来的工作是找到一个合适的步长 $\alpha$ 。首先，我们能想到的就是求解一个单变量的优化命题，让原目标函数在该方向上取得最大的下降量，即
$$\text{min}\quad \phi(\alpha)=f(x_k+\alpha p_k), \alpha >0$$ 但一般来说，得到上面这个优化优化命题的解的代价往往很大，因为即使是单变量优化命题，如果目标函数形状很奇怪的话，如下面 Figure 3.1 ，这个方向上的最优点也是很难求的。

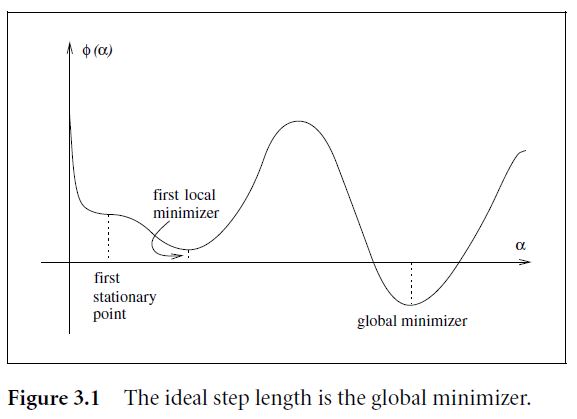
这里要说明的一点是，为了保证算法能最终收敛到极小点，那么对 $\alpha$ 一定是有要求的。比如，如果我们只是单纯保证 $\alpha$ 的选取能使得目标函数之逐步下降的话，那么这是不足够的，例如下图 Figure 3.2，目标函数的最小值是-1。如果我们选取补偿使得目标函数的值以 $f(x_k)=5/k, k=1,2,...$ 这样的级数收敛的话，那么函数值将最终收敛到0而非最优值-1。

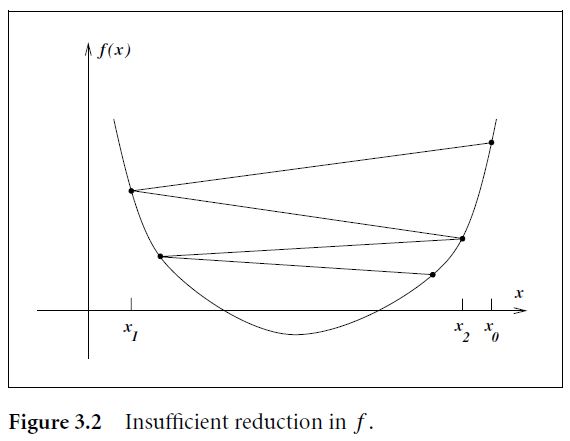
因此，步长