面板数据分析步骤及流程-R语言

最新推荐文章于 2024-06-13 07:30:00 发布

饭饭认认米

最新推荐文章于 2024-06-13 07:30:00 发布

阅读量10w+

点赞数 60

分类专栏： R语言预测模型文章标签： r语言面板数据分析预测

本文链接：https://blog.csdn.net/fanfanrenrenmi/article/details/52222728

版权

面板数据

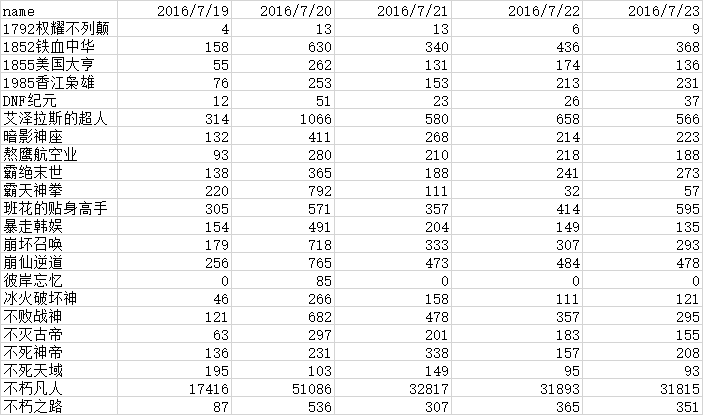
面板数据（Panel Data），也成平行数据，具有时间序列和截面两个维度，整个表格排列起来像是一个面板。
面板数据举例：
这里写图片描述

模型说明及分析步骤

1、首先确定解释变量和因变量；
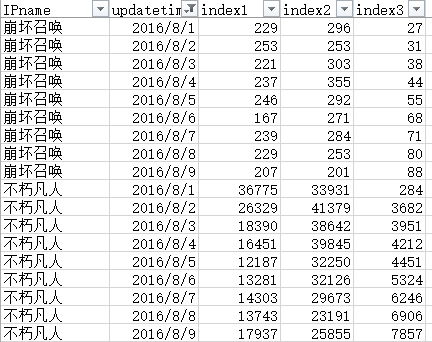
2、R语言操作数据格式，部分截图如下，这里以index3为因变量，index1与index2为解释变量：
这里写图片描述

##加载相关包
install.packages("mice")##缺失值处理
install.packages("plm")
install.packages("MSBVAR")
library(plm)
library(MSBVAR)
library(tseries)
library(xts)
library(mice)
data<-read.csv("F://分类别//rankdata.csv",header=T,as.is=T)##读取数据

2、单位根检验：数据平稳性
为避免伪回归，确保结果的有效性，需对数据进行平稳性判断。何为平稳，一般认为时间序列提出时间趋势和不变均值（截距）后，剩余序列为白噪声序列即零均值、同方差。常用的单位根检验的办法有LLC检验和不同单位根的Fisher-ADF检验，若两种检验均拒绝存在单位根的原假设则认为序列为平稳的，反之不平稳（对于水平序列，若非平稳，则对序列进行一阶差分，再进行后续检验，若仍存在单位根，则继续进行高阶差分，直至平稳，I(0)即为零阶单整，I(N)为N阶单整）。