相机坐标变换

相机坐标变换

世界坐标系指的是系统的绝对坐标，原点是固定的。

相机坐标就是世界坐标根据相机的当前位姿（pos） 变换到相机坐标系下的结果。这个相机位姿包含了旋转矩阵 $R$ 和平移向量 $t$。相机位姿 $R$ ，$t$ 称为相机外参。

像素坐标与成像平面的区别就是，像素坐标的原点在图像的左上角，它与成像平面之间相差了一个缩放和一个原点的平移。

再说相机内参，只需要知道它是一组参数$(f_x,f_y,c_x,c_y)$，其中$f_x,f_y,c_x,c_y$单位都是像素，具体什么意义后面解释。

相机外参由于是相机的位姿，它会随着相机的运动而改变，但是相机内参是不变的。相机外参的估计可以用视觉里程计，相机内参在相机出厂之后是固定的，有的生产厂商会告诉你相机内参，有时需要自己标定（如棋盘格标定法）。

下面以针孔模型相机来说明上面这些概念的关系。

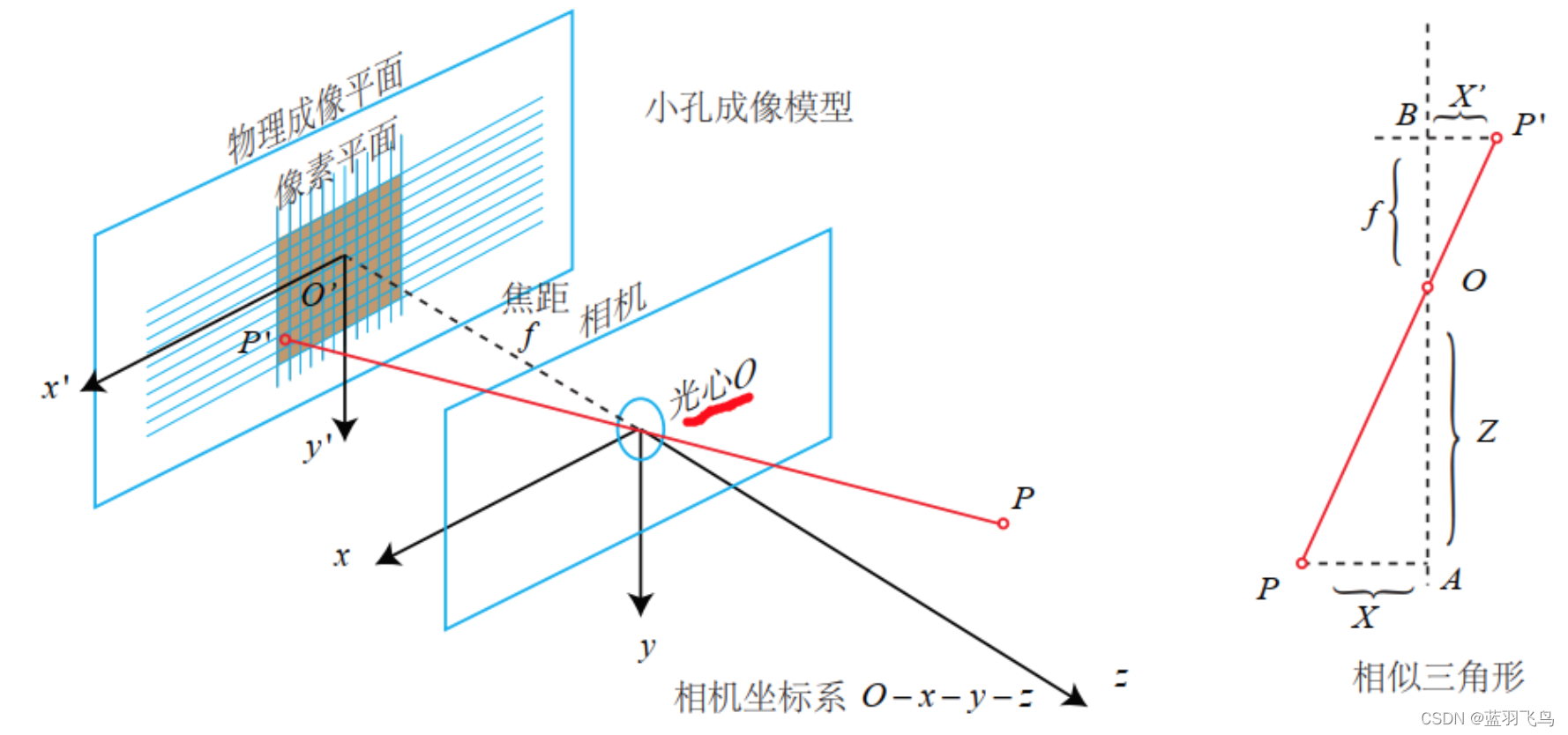
上面的 $P$ 是相机坐标系下的坐标$(X,Y,Z)$。
经过小孔 $O$ 投影之后到成像平面$O’-x’-y’$上的点 $P’$ , $P’$ 的坐标为 $[X’,Y’,Z’]$。

小孔成的是倒像，所以 $\frac{Z}{f}=-\frac{X}{X^{\prime }}=-\frac{Y}{Y^{\prime }}$ ，其中 $f$ 表示焦距。因为实际相机得到的图像并不是倒像，把负号去掉，得到 $\frac{Z}{f}=\frac{X}{X^{\prime }}=\frac{Y}{Y^{\prime }}$，整理一下，得到
$$X^{\prime }=f\frac{X}{Z},Y^{\prime }=f\frac{Y}{Z}$$
$(X,Y,Z)$ 和 $(X’,Y’)$ 这俩坐标的单位可以理解为米，

不过在相机中我们最终获得的是一个个的像素，

所以成像平面上固定着一个像素平面 $o-u-v$, 像素坐标用 $[u,v]$ 表示，成像平面上是 $[X’,Y’]$。

像素坐标系的原点在图像的左上角，$u$ 轴与 $x$ 轴平行，$v$ 轴与 $y$ 轴平行，像素坐标与成像平面之间，相差了一个缩放和一个原点的平移，设在 $u$ 轴上缩放了 $\alpha$ 倍，$v$ 轴上缩放了 $\beta$ 倍，所以呢，得到$u=\alpha X^{\prime }+c_x,v=\beta Y^{\prime }+c_y$

把上面(1)式代进来，同时，令 $f_x=\alpha f{f}_y=\beta f$ , 得到
$$u=f_x\frac{X}{Z}+c_x,v=f_y\frac{Y}{Z}+c_y$$
好了，这个式子足够用了，其中 $(f_x,f_y,c_x,c_y)$ 就是相机内参。当你知道一个点的三维坐标（相机坐标系下，$Z$ 是深度），用上面的(2)式就可以求出它在图像中的像素坐标。

那相机外参 $(R,t)$ 有什么用呢，举个例子吧，现在有相机1 $(R_1,t_1)$ 拍下的图像 $I_1$，然后有一个不同视角的相机2 $(R_2,t_2)$ 拍下了图像 $I_2$，已知 $I_1 $ 中的一个特征点 $p_1$，那这个 $p$ 应该对应 $I_2$ 的哪个点呢（怎么找到 $p_2$)。

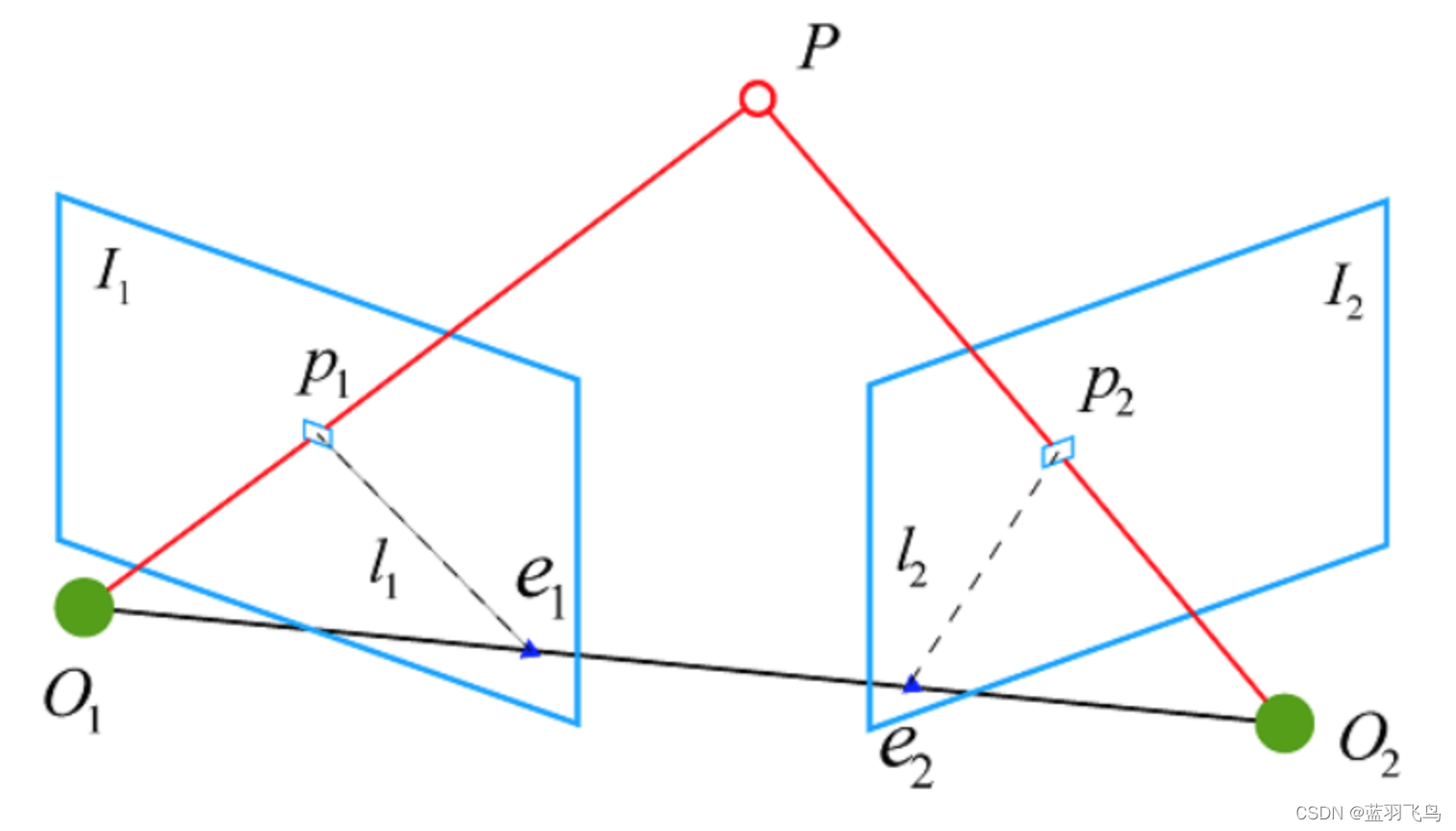
首先利用 $(R_1,t_1)$ 把 $p_1$ 转到世界坐标系，再用 $(R_2,t_2)$ 把世界坐标转为相机2下的 $p_2$ 坐标。

有的相机位姿并没有给 $R$ ，而是 $(q_w,q_x,q_y,q_z,t_x,t_y,t_z)$ 的形式，这就需要把四元数 $(q_w,q_x,q_y,q_z)$ 转为 $R$，再由 $(R,t)$ 得到转换矩阵 $T$。

整体思路：

• $p_1$ 在图片 $I_1$ 上，是像素坐标系，根据camera1的内参把它转到camera1的相机坐标系，得到 $(x_{c1},y_{c1},z_{c1})$,
• 根据camera1的外参把 $(x_{c1},y_{c1},z_{c1})$ 转到 世界坐标系，得到上图中的P点坐标 $(x_{w1},y_{w1},z_{w1})$,
• 根据camera2的外参把P点 $(x_{w1},y_{w1},z_{w1})$ 转到camera2的相机坐标系，得到 $(x_{c2},y_{c2},z_{c2})$ .
• 最后根据camera2的内参 把 $(x_{c2},y_{c2},z_{c2})$ 转到像素坐标系，得到图像 $I_2$ 上的 $p_2$ 点坐标 $(x_2,y_2)$.

整个坐标系的转换关系：像素1 -> 相机1 -> 世界 -> 相机2 -> 像素2

其中，像素坐标系为2D，其他都是3D。

具体步骤：

(1). p1 像素坐标 --> 相机1 坐标

这两个坐标系的关系由相机内参决定,相机内参 $(f_x,f_y,c_x,c_y)$，假设像素坐标为 $(x_1,y_1)$, 相机1坐标为 $(x_{c1},y_{c1},z_{c1})$ , 其中 $z_{c1}$ 为 $I_1$ 的深度图 $(x_{c1},y_{c1})$ 处的值，那么
$$x_1=f_x\frac{x_{c1}}{z_{c1}}+c_x,y_1=f_y\frac{y_{c1}}{z_{c1}}+c_y$$
现在要求 $x_{c1}$ 和 $y_{c1}$, 由（3）得到
$$x_{c1}=(x_1-c_x)\ast z_{c1}/f_x{y}_{c1}=(y_1-c_y)\ast z_{c1}/f_y$$
(2). p1 的相机1 坐标 --> 世界坐标

转换关系： 相机坐标 = T * 世界坐标， 世界坐标 = T-1 * 相机坐标，其中 T 为world -> camera的转换矩阵。

如何求得转换矩阵 T ？先从概念介绍开始，

旋转矩阵R ：3 * 3矩阵

平移向量 t : 3 * 1矩阵

把R 和 t 拼成转换矩阵 T ：4 * 4矩阵，$T=\left[\begin{array}{ccc}R& & t\\ 0^T& & 1\end{array}\right]$

顺便提一下李群李代数，T是SE(3), R是SO(3).

话题回到坐标，$(x_{c1},y_{c1},z_{c1})$ 为相机1坐标，$(x_w,y_w,z_w)$ 为世界坐标，那么世界坐标转相机坐标为：

$$\left[\begin{array}{c}{x}_{c1}\\ y_{c1}\\ z_{c1}\\ 1\end{array}\right]=T\cdot \left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$
你肯定很好奇，为什么要加一维呢？

如果 $T$ 不加最后一行的 $\left[\begin{array}{cc}{0}^T& 1\end{array}\right]$，坐标也不加最后一维的 $1$，直接 $T=\left[\begin{array}{cc}R& t\end{array}\right]$ 也能计算，为什么一定要加一维?$\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]=T\cdot \left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]$ , 这里 $T=\left[\begin{array}{cc}R& t\end{array}\right]$

是这样的，现在是从 世界坐标 转 相机1坐标 ，如果要把 相机1坐标 转 世界坐标 呢？（我们现在要做的就是把 $p_1$ 的 相机1坐标 转到 世界坐标。）

那就需要这么计算了,

$\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]=T^{-1}\cdot \left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]$ ，这里 $T=\left[\begin{array}{cc}R& t\end{array}\right]$，无法求逆矩阵

求 $T$ 的逆矩阵，$T$ 必须是square（行数 = 列数）的，不能是3 * 4, 必须是4 * 4的。

所以加上一行，凑成 4 * 4 矩阵$ T=\begin{bmatrix}R&&t\0^T&&1\end{bmatrix}$

那么 相机坐标 --> 世界坐标 就变为：

$$\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]=T^{-1}\cdot \left[\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}\right]$$
有的程序中会使用 $T_{wc}$, $T_{wc}$ 这样的称呼，这里 $w$ 指world, 是世界坐标，$c$ 指camera, 是相机坐标。$T$ 表示转换矩阵，至于 $T_{wc}$ 是world转camera 还是camera转world, 需要根据实际情况而定（每个开发者习惯不一样）。

实际中，到了这里估计还是不知如何计算 $T$，问题在哪呢？

我们拿到的 相机外参 一般会是一个四元数+平移向量的形式，其中并没有 $R$ 矩阵。相机外参：$(q_w,q_x,q_y,q_z,t_x,t_y,t_z)$, （这个顺序要根据实际情况而定，有的相机顺序并不是这样）。这里用四元数 $q=(q_w,q_x,q_y,q_z)$ 代替了 $R$ 矩阵，原因在于 $R$ 是3 * 3矩阵，有9个量，而一次旋转只有3个自由度，这种表达方式是冗余的，四元数的表达更紧凑。

上面是涉及到的相关概念，现在开始计算 $T$。

现在要先把 $q$ 转为 $R$，再由 $(R,t)$ 得到 $T$。$q=(q_w,q_x,q_y,q_z)$, （一定是 $q_w,q_x,q_y,q_z$ 的顺序，不是的先调整到这个顺序）

$t=(t_x,t_y,t_z)$, 这里要注意 $t$ 的单位，如果是mm, 需要 / 1000.0.

直接计算的话，由四元数 $q$ 到旋转矩阵 $R$ 的公式为：
$$\mathbf{R}=\left[\begin{array}{ccc}1-2q_2^2-2q_3^2& 2q_1{q}_2-2q_0{q}_3& 2q_1{q}_3+2q_0{q}_2\\ 2q_1{q}_2+2q_0{q}_3& 1-2q_1^2-2q_3^2& 2q_2{q}_3-2q_0{q}_1\\ 2q_1{q}_3-2q_0{q}_2& 2q_2{q}_3+2q_0{q}_1& 1-2q_1^2-2q_2^2\end{array}\right]$$

这里 $q_0,q_1,q_2,q_3$ 分别对应 $q_w,q_x,q_y,q_z$，结合 $(t_x,t_y,t_z)$, 下面再加一行 $\left[\begin{array}{cc}{0}^T& 1\end{array}\right]$，得到 $T_1$ （由相机1的外参得到）。

已经得到了T1，下面可把相机坐标转为世界坐标
$$\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]=T_1^{-1}\cdot \left[\begin{array}{c}{x}_{c1}\\ y_{c1}\\ z_{c1}\\ 1\end{array}\right]$$
(3). 世界坐标 --> 相机2坐标

上面已经说明了如何由 世界坐标 转 相机坐标。注意上面求的 $T_1$ 是由相机1的外参得到，这里要用到相机2的外参，camera2: $ (q_{w2}, q_{x2}, q_{y2}, q_{z2}, t_{x2}, t_{y2}, t_{z2})$,求得 $T_2$ 后，由下式得到 $P$ 的相机2坐标
$$\left[\begin{array}{c}{x}_{c2}\\ y_{c2}\\ z_{c2}\\ 1\end{array}\right]=T_2\cdot \left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$
(4) 相机2坐标 --> 像素坐标2

相机内参 $(f_x,f_y,c_x,c_y)$
$$x_2=f_x\frac{x_{c2}}{z_{c2}}+c_x,y_2=f_y\frac{y_{c2}}{z_{c2}}+c_y$$
这样就得到了图像 $I_2$ 上的映射点 $p_2$ 的坐标。