从贝叶斯滤波理论到容积卡尔曼滤波算法（CKF）详细推导及编程实现常转弯率模型估计。（matlab）

容积卡尔曼滤波（CKF）是由加拿大学者Arasaratnam和Haykin在2009年提出的。该算法的核心思想是针对非线性高斯系统，通过三阶球面径向容积准则来近似状态的后验均值和协方差，以保证在理论上以三阶多项式逼近任何非线性高斯状态的后验均值和方差。

• 贝叶斯滤波
• 球面-径向容积规则
• 容积卡尔曼滤波算法
• matlab实现"Cubature Kalman Filters"论文中常转弯率例子

贝叶斯滤波：

由于容积卡尔曼滤波是基于贝叶斯滤波理论框架的次优滤波，所以我们先来了解一下贝叶斯滤波。

在解决滤波问题时，如果我们能求出状态的后验概率密度函数，就可以通过状态的概率密度函数描述非线性系统的统计特性，再通过各种估计准则和近似方法就能得到不同的滤波算法。
系统状态后验概率密度决定了系统的多种统计特性。因此如何求得系统状态的后验概率密度函数成为关键。而贝叶斯估计的优点是给出了状态后验概率密度函数的递推求解方法，成为众多滤波算法的核心思想。

上面两个式子就组成了贝叶斯递推公式，我们可以看出贝叶斯滤波从理论上实现了非线性滤波的最优估计。

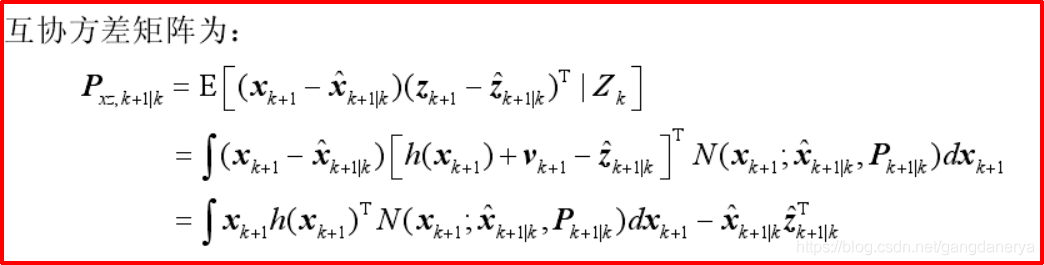
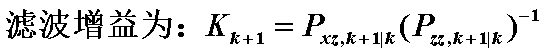
下图为贝叶斯滤波框图。

球面-径向容积规则：

由上一部分的贝叶斯滤波，我们很难直接求解上述积分。我们将上述积分变形为：

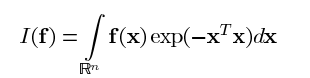
n维球坐标变换

由n维球坐标变换定理可将上面积分转换成球面径向积分：


将上面积分分解成球面积分和径向积分：


上述球面积分和径向积分都是通过容积规则来实现，容积规则是将一系列点集D用非线性函数进行传递，然后根据加权求和来近似非线性函数的后验均值和方差。
*

点集D有如下定义：

所以球面积分就变成了：




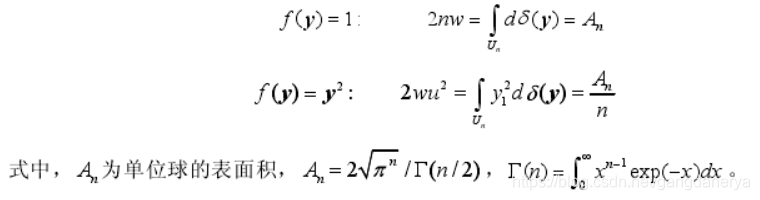
所以容积点可选取单位球的球面与其坐标系相交的点。
所以球面积分可近似为：

径向积分：

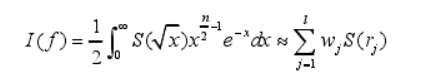
将球面积分的近似带入到径向积分中可得：


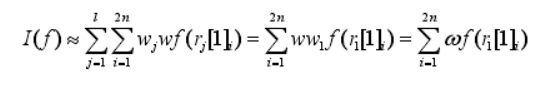
上面式子就是三阶球面径向容积规则的近似规则。
接下来我们将容积规则与高斯分布的积分相结合：



上面式子就是容积卡尔曼滤波使用的三阶球面径向容积规则。

接下来我们来看一下CKF算法的流程：

常转弯率模型CKF滤波估计（matlab）:

程序如下：

CKF函数：

function [Pk,Xjian]=CKF(Pk,n,Xjian,y,Q,R)
m = 2*n;  %n为状态维数
T=1;%时间
kesai=sqrt(m/2) * [eye(n),-eye(n)];
[S1]=chol(Pk)';%分解成AT*A（下三角*上三角）取下三角
Xr=S1*kesai+repmat(Xjian,1,m);%计算容积点,repmat()把元素复制m行n列
for i=1:m
    omiga = Xr(5,i);
    fai= [1,     sin(omiga*T)/omiga, 0, -(1-cos(omiga*T))/omiga, 0;
          0,           cos(omiga*T), 0,           -sin(omiga*T), 0;
          0, (1-cos(omiga*T))/omiga, 1,      sin(omiga*T)/omiga, 0;
          0,           sin(omiga*T), 0,            cos(omiga*T), 0;
          0,                      0, 0,                       0, 1];
    Xcr(:,i) = fai*Xr(:,i);  %传播容积点                                 
end 
Xpr=(1/m).*sum(Xcr,2);%状态量预测值
Ppr=(1/m).*(Xcr*Xcr')-Xpr*Xpr'+ Q;%误差协方差
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[S2]=chol(Ppr)';
Xp=S2*kesai+repmat(Xpr,1,m);
yr=[sqrt(Xp(3,:).^2+Xp(1,:).^2);atan2(Xp(3,:),Xp(1,:))];%传播

Ypre = (1/m).*sum(yr,2);%计算量测预测值
Pyy=(1/m)*yr*yr'-Ypre*Ypre'+R;%协方差
Pxy=(1/m)*Xp*yr'-Xpr*Ypre';%互协方差

K = Pxy*inv(Pyy); %增益                             
Xjian=Xpr+K*(y-Ypre);  % 状态估计                       
Pk=Ppr-K*Pyy*K';  %估计误差协方差

主函数：

clear all;
clc;
bushu=100;
omiga=-3;
T=1;
q1=0.1,q2=1.75*10^(-4);
or=10,oo=sqrt(10);
M=[(1/3)*T^2 (1/2)*T^2;(1/2)*T^2 T]
R=diag([(or)^2 (oo)^2]);
randn('seed',36);     w1=sqrt(q1*M)*randn(2,2);
randn('seed',32);     w2=sqrt(q1*M)*randn(2,2);
randn('seed',29);     w3=sqrt(q2*T)*randn(1,1);
Q=zeros(5,5);
Q(1,1)=w1(1,1),Q(1,2)=w1(1,2),Q(2,1)=w1(2,1),Q(2,2)=w1(2,2);
Q(3,3)=w2(1,1),Q(3,4)=w2(1,2),Q(4,3)=w2(2,1),Q(4,4)=w2(2,2);
Q(5,5)=w3;

 x(:,1) =[1000;300;1000;0;-3];
 Pk(:,:,1) =diag([100,10,100,10,100]); 
Xjian(:,1)=[1000;300;1000;0;-3];
n=5;
    randn('seed', 5);  
    w=sqrt(Q)*randn(5,bushu);
    randn('seed', 2);
    v=sqrt(R)*randn(2,bushu);
 for k = 2 : bushu
    omiga=x(5,k-1);
    fai=[1,    sin(omiga*T)/omiga,      0,    -(1-cos(omiga*T))/omiga,     0;
         0,    cos(omiga*T),            0,    -sin(omiga*T),               0;
         0,    (1-cos(omiga*T))/omiga,  1,    sin(omiga*T)/omiga,          0;
         0,    sin(omiga*T),            0,    cos(omiga*T),                0;
         0,    0,                       0,    0,                           1];
 
    x(:,k) = fai * x(:,k-1) +w(:,k-1);      %状态值 
    z(:,k) = [sqrt(x(1,k).^2+x(3,k).^2);atan2(x(3,k),x(1,k))] + v(:,k) %观测值
     
    [Pk(:,:,k),Xjian(:,k)]=CKF(Pk(:,:,k-1),n,Xjian(:,k-1),z(:,k),Q,R);
 end

t=2:bushu;
figure(1)
subplot(2,2,1)
plot(t,x(3,t),'b',t,Xjian(3,t),'r');  
xlabel('时间'); 
ylabel('水平位置');
subplot(2,2,2)
plot(t,x(2,t),'b',t,Xjian(2,t),'r');
xlabel('时间'); 
ylabel('水平速度');
subplot(2,2,3)
plot(t,x(3,t),'b',t,Xjian(3,t),'r');  
xlabel('时间'); 
ylabel('竖直位置');
subplot(2,2,4)
plot(t,x(4,t),'b',t,Xjian(4,t),'r');
xlabel('时间'); 
ylabel('竖直速度');
figure(2)
plot(t,x(5,t),'b',t,Xjian(5,t),'r');
legend('真值','估值'); 
xlabel('时间'); 
ylabel('转弯率');
figure(3)
plot(x(1,t),x(3,t),'b',Xjian(1,t),Xjian(3,t),'r');
 

运行结果如下：

补充说明：

1，因为在这个例子中系数fai是变化的，所以在编CKF函数的程序时要将fai的变化也体现出来（看第一段程序）。 2，看最后一张图我们发现估值跟的效果不是特别好可能是因为初始值过大，程序中随机数种子的选取（种子的选取不同结果也不相同，主要改变一下w3的种子）。

Help
最后本人在找关于CKf 文章中常转弯率模型的推导尤其是其中M的详细推导过程，希望大家多多分享，万分感谢！请收下小弟的膝盖，哈哈哈