工程设计1任务书1 浮球液位控制系统

因菜入味

已于 2023-11-26 19:36:52 修改

阅读量298

点赞数

文章标签：数据库服务器运维

于 2023-11-24 15:37:24 首次发布

本文链接：https://blog.csdn.net/goal_achieving/article/details/134504745

版权

文章讨论了液位控制系统的动态模型，包括微分方程建立、传递函数设计，以及针对扰动的时域性能分析。涉及根轨迹校正方法，针对稳定与不稳定系统的设计与校正，并利用MATLAB进行仿真和先进控制算法的应用研究。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题目

下图所示为液位控制系统，假设稳态输入流量为Q，稳态输出流量为Q，稳态水头为H，稳态导阀的位移为X=0，稳态阀的位置为Y。假设定点R对应于稳态水头H，设定点是固定的。又假设扰动输入流量qd在t=0时刻作用于水箱，qd的量值很小。

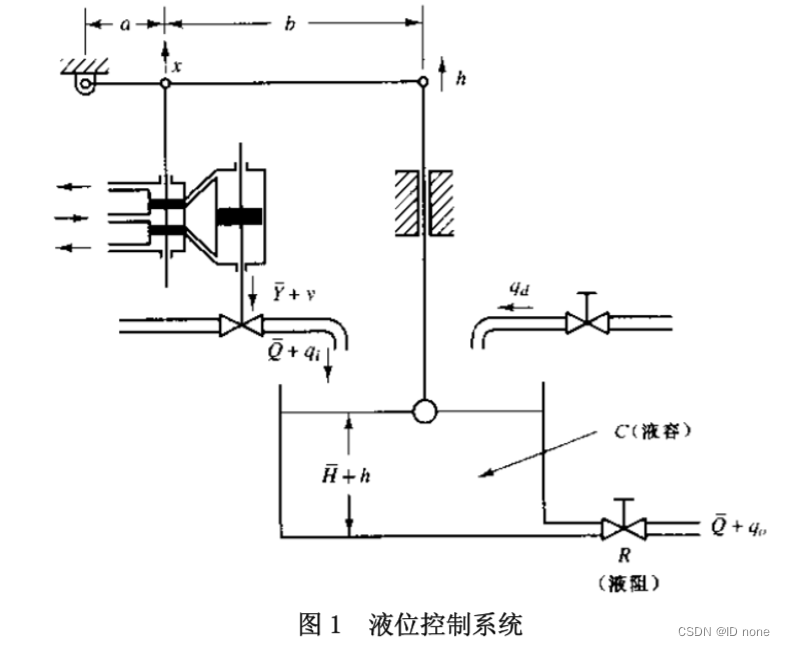
要求：

分析系统工作过程，建立系统的传递函数，并画出结构图；
当扰动输入量qd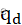为单位阶跃函数时，试分析系统的时域性能；
当系统不稳定时，用根轨迹校正系统并确定系统校正装置参数，画出系统波特图，指出校正方法；如果系统是稳定的，那么就设计一个不稳定系统，用根轨迹进行分析并确定系统校正装置参数，画出系统波特图，指出校正方法；
设计、校正结果验证；
运用MATLAB仿真控制系统，附程序代码；
查阅相关文献，探讨先进控制算法在该系统中的应用。

下图所示为液位控制系统，假设稳态输入流量为Qi，稳态输出流量为Qo，稳态水位为H，稳态导阀的位移为X=0，稳态阀的位置为Y。假设定点R对应于稳态水头H，设定点是固定的。又假设扰动输入流量qd在t=0时刻作用于水箱，qd的量值很小。

分析系统工作过程

水流入量Qi(Quatity in)

水流出量Qo

稳态水位高度H。反映了水的流入流出之间的平衡关系。显然，当流入量多于流出量时，h增加，浮球上升，通过连杆调节调节阀Y，以减少出水量使液位稳定；反之亦然

调节阀位置Y，同时用Y代指调节阀本身

Q为输入输出水流量稳态值

qd为扰动输入流量

h为液位增量

v为稳态阀增量

R为液阻

C为液容

当Qi不等于Qo时。例如H+h增加时，浮子升高，使稳压阀减小阀门开度，进入时间的流量减少；反之，当H+h减小时，系统会增大稳压阀的阀门开度，加大流入水量，使液位升到给定高度。

系统方块图

符号含义

Qi：水流入量
Qo：水流出量
R：液阻
C：液容
H：稳态水位
Y：调节阀位置
+h：液位增量
+v：稳态阀增量
-v：稳态阀减量
qd:扰动流入量

杠杆和稳压阀中间还需要一个导阀

微分方程建立

首先，定义输入和输出的偏差：

\[\Delta Q = Q - Q_o\] （输入流量偏差）
\[\Delta H = H - R\] （液位偏差）

然后，我们可以根据系统的物理原理列出微分方程：

\[\frac{dH}{dt} = \frac{1}{C} \cdot (\Delta Q - \Delta Q_d)\] （液位变化率）

其中，
- \(\frac{dH}{dt}\) 表示液位的变化率；
- \(C\) 表示液容；
- \(\Delta Q\) 表示输入流量偏差；
- \(\Delta Q_d\) 表示扰动输入流量偏差。

同时，我们还需要考虑调节阀的动态响应。假设调节阀的动态方程为：

\[\frac{dY}{dt} = k \cdot (\Delta H - X)\] （调节阀位移变化率）

其中，
- \(\frac{dY}{dt}\) 表示调节阀位移的变化率；
- \(k\) 表示调节阀的增益；
- \(\Delta H\) 表示液位偏差；
- \(X\) 表示稳态导阀的位移。

需要注意的是，根据假设，稳态时导阀的位移为 \(X = 0\)，所以动态方程中的 \(\Delta H - X\) 简化为 \(\Delta H\)。

综上所述，浮球液位控制系统的微分方程为：

\[\frac{dH}{dt} = \frac{1}{C} \cdot (\Delta Q - \Delta Q_d)\]
\[\frac{dY}{dt} = k \cdot \Delta H\]