半导体器件与物理篇4 双极型晶体管及其器件

双极型晶体管的工作原理

双极型晶体管的结构：双极型器件是一种电子和空穴均参与导通过程的半导器件。由两个相邻的耦合p-n结组成。其结构可为pnp或npn的形式

pnp双极型晶体管三段掺杂区的特点：
1.发射区(emitter,E)，浓度最高的$p^{+}$区
2.基区(base,B)，浓度中等的较窄的n区
3.集电区(collector,C)，浓度最小的p区

放大模式下的晶体管

下图为工作在放大模式下的共基组态pnp晶体管。共基组态的含义是：输入和输出电流共用基极。

首先我们要明确，如果射基结和集基结相距足够远，也就是基极过宽，那么晶体管与两个二极管的反向串联就没有什么区别。
所以，晶体管的基区宽度必须足够小，使得发射极进入基区的空穴通过扩散作用就来到了集基结边。然后在集基结的反向偏压的作用下，被带到了集电极。因此，发射极的含义是发射载流子的意思，而集电极的意义是接受从发射极那边来的载流子。

电流增益

$\{\begin{array}{l}{I}_{BB}=I_{Ep}-I_{Cp}=I_E=I_{Ep}+I_{En}\\ I_C=I_{Cp}+I_{Cn}\\ I_B=I_E-I_C=I_{En}+(I_{Ep}-I_{Cp})-I_{Cn}\end{array}$
由基区注入发射区的电子电流$I_{En}$；集电结附近因热所产生的由集电区流往基区的电子电流$I_{Cn}$
发射效率，可以理解为发射极的多子在发射极的所有载流子中的电流占比：$\gamma =\frac{I_{Ep}}{I_E}=\frac{I_{Ep}}{I_{Ep}+I_{En}}$

基区输运系数，是集电极收集的多子电流与发射极发射的多子电流之比：${\alpha }_T=\frac{I_{Cp}}{I_{Ep}}$

共基电流增益，是集电极多子的电流与发射极所有载流子的电流之比，也等于发射效率与基区输运系数之积：${\alpha }_0=\gamma \cdot {\alpha }_T=\frac{I_{Ep}}{I_E}\cdot \frac{I_{Cp}}{I_{Ep}}=\frac{I_{Cp}}{I_E}$

共基电流增益为什么是这个比值呢？发射极发射的所有载流子，与集电区集电的有效部分——即多子电流之间的比值。

共基组态的集电极电流：$I_C={\alpha }_0{I}_E+I_{CBO}$
$I_{CBO}$是发射极断路时(即$I_E=0$)集基(b.c)极间的电流

双极型晶体管的静态特性

为推导出理想晶体管的电流和电压，假设如下:
(1)晶体管中各区域的浓度为均匀掺杂;
(2)基区中的空穴漂移电流和集基极反向饱和电流可以忽略;
(3)载流子注入属于小注入;
(4)耗尽区中没有产生-复合电流;
(5)晶体管中无串联电阻。

分析基区区域

已由于第2条假设“基区中的空穴漂移电流和集基极反向饱和电流可以忽略;”和第4条假设“耗尽区中没有产生-复合电流;”，所以我们简化稳态连续性方程式，得到无电场的稳态连续性方程：$\frac{d^2{p}_n}{d{x}^2}-\frac{p_n-p_{n0}}{D_p{\tau }_p}=0$
少子的扩散系数$D_p$，少子寿命${\tau }_p$，扩散长度$L_p=\sqrt{D_p{\tau }_p}$

求解这个二阶微分方程，可以得到一般解的形式：$p_n(x)=p_n+C_{1}exp(\frac{x}{L_p})+C_{2}exp(-\frac{x}{L_p})$

为了求得一般解表达式中的两个位置参数$C_1,C_2$，我们需要取了个一致的$p_n(x)$。于是，我们提出两个边界条件：
1.第一个边界条件表示在正向偏压的状态下，射基结的耗尽区边缘(x=0)的少数载流子浓度是热平衡状态下的值乘上$exp(\frac{q{V}_{EB}}{kT})$
由此我们得到正向偏压下，射基结耗尽区边缘的少数载流子浓度为：$p_n(0)=p_{n0}exp(\frac{q{V}_{EB}}{kT})$
热平衡状态下基区的少子浓度$p_{n0}$
2.第二个边界条件表示在反向偏压的状态下，集基结耗尽区边缘(x=W)少数载流子浓度为零。
由此我们得到第二个方程:$p_n(W)=0$

将这两个方程代入，求解两个未知量$C_1,C_2$，可以得到反向偏压下，集基结耗尽区边缘的少数载流子浓度为0时，射基结耗尽区边缘的载流子浓度约为：$p_n(x)=p_{n0}exp(\frac{q{V}_{EB}}{kT})(1-\frac{x}{W})=p_n(0)(1-\frac{x}{W})由简化后的$p_n(x)$的表达式，我们可以观察到：少数载流子的分布趋近于一直线。

分析发射极和集电极区域

发射区和集电区中的少数载流子分布可以用类似上述基区情况的方法求得。在图中，发射区与集电区中性区域的边界条件为：$\{\begin{array}{l}{n}_E(x=-x_E)=n_{EO}exp(\frac{q{V}_{EB}}{kT})\\ N_C(x=x_c)=N_{CO}exp(-\frac{q|V_{CB}|}{kT})=0\end{array}$

其中$n_{EO}$和$n_{CO}$分别为发射区和集电区中热平衡状态下的电子浓度。设发射和集电区的宽度分别远大于扩散长度$L_E$和$L_C$，最终得到：$n_E(x)=n_{EO}+n_{EO}[exp(\frac{qVEB}{kT})-1]exp(\frac{x+x_E}{L_R}),x<=-x_E$

放大模式下理想晶体管的电流

基区宽度要小。定量表达基区宽度小的表示式为$w/L_p<<1$。

由发射区注入基区的空穴电流与少子浓度分布的梯度成正比：$I_{Ep}\approx \frac{qA{D}_p{p}_{n0}}{W}exp(\frac{q{V}_{EB}}{kT})$
在图中的W处由集电极收集到的空穴电流为：$I_{Cp}\approx \frac{qA{D}_p{p}_{n0}}{W}exp(\frac{q{V}_{EB}}{kT})$
$I_{Ep}$与$I_{Cp}$的表达式相等。
晶体管有效横截面面积A；基区宽度W；

由基区流向发射区的电子流为：$I_{En}=\frac{qA{D}_E{n}_{EO}}{L_E}[exp(\frac{q{V}_{EB}}{kT})-1]$
由集电区流向基区的电子流为：$I_{Cn}=\frac{qA{D}_C{n}_{CO}}{L_C}$
电子在发射区的扩散系数$D_E$；电子在集电区的扩散系数$D_C$。
发射极电流为$I_{Ep}$和$I_{En}$的和：$I_E=I_{Ep}+I_{En}=\frac{qA{D}_p{p}_{n0}}{W}exp(\frac{q{V}_{EB}}{kT})+\frac{qA{D}_E{n}_{EO}}{L_E}[exp(\frac{q{V}_{EB}}{kT})-1]$

工作模式

在放大模式下，射基结是正向偏压，集基结是反向偏压。

在饱和模式下，品体管中的两个结都是正向偏压，导致两个结的耗尽区中少数载流子分布并非为零。因此在x=W处的边界条件变为：$p_n(W)=p_{n0}exp(\frac{q{V}_{CB}}{kT})$
在饱和模式下，极小的电压就产生了极大的输出电流，晶体管处于导通状态，类似于开关短路(亦即导通)的状态。

在截止模式下，晶体管的两个结皆为反向偏压，边界条件变为$p_n(0)=p_n(W)=0$，截止模式下的晶体管可视为开关断路(或是关闭)。

在反转模式下，射基结是反向偏压，集基结是正向偏压。在反转模式下品体管的集电极用作发射极而发射极用作集电极，相当于晶体管被倒过来用，但是在反转模式下的电流增益通常较放大模式小，这是因为集电区掺杂浓度较基区浓度小，造成低的“发射效率”所致。

共射组态晶体管的电流-电压特性

肯定有疑惑，为什么要定义一个共基电流增益${\alpha }_0$呢？是因为使用共基电流增益能很方便地表示出集电极电流与发射极电流的关系式：$I_C={\alpha }_0{I}_E+I_{CBO}={\alpha }_0(I_B+I_C)+I_{CBO}$
进一步换算得到：$I_C=\frac{{\alpha }_0}{1-{\alpha }_0}{I}_B+\frac{I_{CBO}}{1-{\alpha }_0}$

我们提取上式中$I_B$的系数，定义共射电流增益，-为$I_C$对$I_B$的微分：${\beta }_0=\frac{\Delta I_C}{\Delta I_B}=\frac{{\alpha }_0}{1-{\alpha }_0}$

定义集电极与发射极之间的漏电流为$I_{CEO}$，其表达式满足：$I_{CEO}=\frac{I_{CBO}}{1-{\alpha }_0}=\frac{1-{\alpha }_0+{\alpha }_0}{1-{\alpha }_0}{I}_{CBO}=(1+{\beta }_0)I_{CBO}$
其中$alph{a}_0$可以认为是在描述集电极电流与发射极电流之间的相近程度。二者越相近，则${\alpha }_0$越大，基区$I_B$的电流就越小。
因为${\alpha }_0$一般非常接近于1，使得${\beta }_0$远大于1，所以基极电流的微小变化将造成集电极电流的剧烈变化。

由此可得：$I_C={\beta }_0{I}_B+I_{CEO}$

在一共射组态的理想晶体管中，当$I_B$固定且$V_{EC}>0$时，集电极电流与$V_{EC}$不相关。

当集电极和基极间的反向偏压增加时，基区的宽度将会减少，导致基区中的少数载流子浓度梯度增加，亦即使得扩散电流增加，因此$I_C$也会增加.

厄雷效应

厄雷效应：$I_C$随着$V_{EC}$的增加而增加，或称为基区宽度调制效应。
厄雷电压：将集电极电流往左方延伸，与$V_{EC}$轴相交得到的交点。

双极型晶体管的频率效应与开关特性

跨导的表达式：$g_m={\tilde{i}}_C/{\tilde{v}}_{EB}$

射基结的跨导：${\tilde{i}}_B/{\tilde{v}}_{EB}$

射集结的跨导：${\tilde{i}}_C/{\tilde{v}}_{EC}$

在高频信号下的共基电流增益为：$\alpha =\frac{\alpha }{1+j(f/f_{alpha})}$
${\alpha }_0$为低频（或直流）共基电流增益${\alpha }_0$；共基截止频率$f_{\alpha }$

若满足$f=f_{\alpha }$，则$\alpha =0.707{\alpha }_0（下降3dB)$

在高频信号下，共射电流增益的表达式为：$\beta =\frac{\alpha }{1-\alpha }=\frac{{\beta }_0}{1+j(f/f_{\beta })}$
式中的共射截止频率$f_{\beta }=(1-{\alpha }_0)f_{\alpha }$

截止频率$f_T$，又称为特征频率，定义为：$\beta$的绝对值变为1时的频率。得到：$f_T=\sqrt{{\beta }_0^2-1}{f}_{\beta }\approx {\beta }_0(1-{\alpha }_0)f_{\alpha }\approx {\alpha }_0{f}_{\alpha }$

改善频率响应的方法

要改善频率响应，必须缩短少数载流子穿越基区所需的时间，所以高频晶体管都1.设计成短基区宽度；另一个降低基区渡越时间的方法时2.利用有内建电场的缓变掺杂基区。

异质结双极型晶体管

首先，我们已知在共基放大状态时的晶体管满足：$\{\begin{array}{l}\gamma =\frac{I_{Ep}}{I_E}=\frac{I_{Ep}}{I_{Ep}+I_{En}}//{\alpha }_T=\frac{I_{Cp}}{I_{Ep}}//{\alpha }_0=\gamma \cdot {\alpha }_T=\frac{I_{Cp}}{I_E}\end{array}$

然后又已知共射放大状态的晶体管满足：共射电流增益${\beta }_0=\frac{{\alpha }_0}{1-{\alpha }_0}=\frac{\gamma {\alpha }_T}{1-\gamma {\alpha }_T}$

由${\alpha }_T\approx 1$可以推导出：${\beta }_0=\frac{1-\gamma }{\gamma }$

我也不知道用了什么方法，得到了$\gamma$和 基区射区的扩散系数、两区的少子浓度和射区的扩散长度，得到：$\gamma =\frac{1}{1+\frac{D_E}{D_n}\cdot \frac{p_{E0}}{n_{p0}}\cdot \frac{v_0}{L_E}}$

将$\gamma$代入后，得到共射电流增益的表达式：$\frac{1}{\frac{D_E}{D_n}\cdot \frac{p_{E0}}{n_{p0}}\cdot \frac{v_0}{L_E}}\approx \frac{n_{p0}}{p_{E0}}$
基区热平衡时的少子浓度$n_{p0}$；
发射区热平衡时的少子浓度$p_{E0}$：$p_{E0}=\frac{n_{iE}^2}{N_E}=\frac{N_C{N}_{V}exp(-\frac{E_{gE}}{kT})}{N_E}$
发射区掺杂浓度$N_E$；发射区材料的本征费米能级$n_{iE}$；导带的有效态密度$N_C$；价带的有效态密度$N_V$；发射区材料的禁带宽度$E_{gE}$

回顾共射电流增益的表达式：${\beta }_0\approx \frac{n_{p0}}{p_{E0}}$
其中$p_{E0}$我们已经确定了。因此我们使用求取$p_{E0}$相同的方法，可以得到基区热平衡时的少子浓度：$n_{p0}=\frac{n_{iB}^2}{N_B}=\frac{N_C{N}_{V}exp(-\frac{E_{gB}}{kT})}{N_B}$

将$p_{E0}$和$n_{p0}$代入${\beta }_0$的表达式，可以得到：${\beta }_0\propto \frac{N_E}{N_B}exp(\frac{E_{gE}-E_{gB}}{kT})=\frac{N_E}{N_B}exp(\frac{\delta E_g}{kT})$

由以上的推导，我们可以得出最终的结论：${\beta }_0$同时受发射区基区的浓度比，以及两区杂质种类的影响。

同质结和异质结的不同：同质结的双极型晶体管的组成材料相同，发射区和基区间并无禁带宽度差存在，所以必须将两区的掺杂浓度提到很高；异质结的双极型晶体管由于组成材料不同，发射区和基区材料间具有极大的禁带宽度差，可以提高共射电流增益${\beta }_0$

异质结双极型晶体管(HBT)

异质结双极型晶体管(HBT)是指品体管中的一一个或两个结由不同的半导体材料所构成。
HBT的主要优点：发射效率较高；具有较高的速度，可以工作在更高的频率。

穿通效应的定义：未知。

先进的HBT

InP/GaAs具有非常低的表面复合，电子迁移率较GaAs，高频特性好，其截止频率可高达550GHz，集电极在强电场时比GaAs集电极具有更高的漂移速率，其击穿电压亦比GaAs集电极高。

可控硅器件及相关功率器件

可控硅器件的定义：一种非常重要的功率器件，可用来作高电压和高电流的控制，使器件从关闭或阻断的状态转换为开启或导通的状态，反之亦然。
可控硅器件的结构如图：

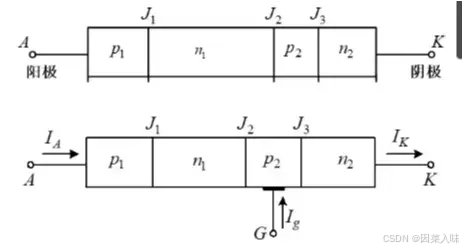
图中第一个器件由三个串接的p-n结J、J2、J组成。与接触电极相连的最外一p层称为阳极，另一边的n层称为阴极。这个没有额外电极的结构是个两瑞点的器件,被称为p-n-p-n二极管。若另一称为栅极的电极被连到内层的p2层，所构成的三端点器件一般称为可控硅器件。

双向可控硅器件：双向可控硅器件是一种在正或负阳极电压下皆可以开或关的开关器件。

什么是负电阻区域？什么是负电阻器件？什么是整流器件？

习题

例1:已知在一理想晶体管中，各电流成分为：$I_{Ep}=3mA、I_{En}=0.01mA、I_{Cp}=2.99mA、I_{Cp}=0.001mA$。试求出下列各值:(a)发射效率$\gamma$;(b)基区输运系数${\alpha }_T$;©共基电流增益${\alpha }_0$;(d)$I_{CB0}$。
需要用到的公式包括1.发射效率计算式$\gamma =\frac{I_{Ep}}{I_E}=\frac{I_{Ep}}{I_{Ep}+I_{En}}$ 2.基区输运系数计算式${\alpha }_T=\frac{I_{Cp}}{I_{Ep}}$ 3.共基电流增益计算式${\alpha }_0=\gamma \cdot {\alpha }_T$ 4.发射极电流计算式 5.集电极电流计算式 6.集电极电流与集基极漏电流的关系式$I_C={\alpha }_0{I}_E+I_{CBO}$;$I_{CBO}$是发射极断路时(即$I_E=0$)集基(b.c)极间的电流

例2:一个理想的p*-n-p晶体管，其发射区、基区和集电区的掺杂浓度分别为$10^{19}c{m}^3、10^{17}c{m}^{-3}和5\times 10^{15}c{m}^3$，而寿命分别为$10^{-8}s、10^{-7}s和10^{-6}s$，假设有效横截面面积A为$0.05m{m}^2$，且射基结正向偏压在0.6V，试求晶体管的
共基电流增益。其他晶体管的参数为$D_E=1c{m}^2/s、D_p=10c{m}^2/s、Dc=2c{m}^2/s、W=0.5\mu m$。
需要用到的公式包括1.扩散长度的计算式 2.深掺杂区的少子浓度与轻掺杂区掺杂浓度的关系式$\frac{n_i^2}{N_B}$;热平衡状态下基区的少子浓度$n_{E0}=\frac{n_i^2}{N_E}$ 3.结内少子浓度与轻掺杂区掺杂浓度的关系式$n_{C0}=\frac{n_i^2}{N_C}$ 4.由发射区注入基区的空穴电流$I_{Ep}\approx \frac{qA{D}_p{p}_{n0}}{W}exp(\frac{q{V}_{EB}}{kT})$ 5.由集电极收集到的空穴电流$I_{Cp}=I_{Ep}6.由基区流向发射区的电子流$I_{En}=\frac{qAD_En_{EO}}{L_E}[exp(\frac{qV_{EB}}{kT})-1]$；由集电区流向基区的电子流为：$I_{Cn}=\frac{qAD_Cn_{C0}}{L_C}$ 7.共基电流增益的计算式

例3:已知在一理想晶体管中，各电流成分为$I_{Ep}=3mA、I_{En}=0.01mA、I_{Cp}=2.99mA、I_{Cn}=0.001mA$。求出共射电流增益${\beta }_0$，并以${\beta }_0$和$I_{CBO}$表示$I_{CEO}$，并求出$I_{CEO}$的值。
需要用到的公式包括1.发射效率计算式 2.基区输运系数计算式 3.共基电流增益 4.用共基电流增益表示的集电极电流与发射极电流关系式$I_{CE0}={\beta }_0{I}_{CB0}+I_{CB0}$ 5.共射电流增益计算式${\beta }_0=\frac{{\alpha }_0}{1-{\alpha }_0}$