热平衡时的PN结
pn结的定义:由p型半导体和n型半导体接触形成的结
pn结的特性和关键变量包括:整流性(即电流单向导通的特性)、平衡费米能级(费米能级 E F E_F EF为常数, d E F d x = 0 \frac{dE_F}{dx}=0 dxdEF=0)、内建电势 V b i V_{bi} Vbi、空间电荷区(亦称为耗尽层)
我们将从这些性质入手,由浅入深、从定性到定量的角度去探讨pn结
PN结特性1:整流性
pn结的整流性,即只允许电流单向导通
结击穿:当施以反向偏压时,随反向偏压的增加几乎没有任何电流,电流变化很小,直到一临界电压后电流才突然增加。这种电流突然增加的现象称为结击穿。
pn结特性2:费米能级 E F E_F EF为常数,即 d E F d x = 0 \frac{dE_F}{dx}=0 dxdEF=0
产生原因:在热平衡时,也就是在给定温度之下,没有任何外界扰动,流经pn结的电子电流和空穴电流都为零。因此,对于每一种载流子,电场造成的漂移电流必须与浓度梯度引起的扩散电流完全抵消。
关键公式: d E F d x = 0 \frac{dE_F}{dx}=0 dxdEF=0
由公式可以得到:在热平衡时,PN结内部的费米能级相同

(PS:能带图在保证各自的费米能级相同时,导带底部和价带顶部会进行一个渐变的变化)
pn结特性3:内建电势 V b i V_{bi} Vbi
内建电势 V b i V_{bi} Vbi的推导思路
我们现在理一下思路。假如现在有两块半导体a和b,全部都是本征半导体。
a和b拼在一起则电势差为零,也没有了内建电势。
那什么时候有电势差呢?
我对半导体a掺入了受主杂质,使其空穴浓度迅猛增加;此时我即使不对b进行操作,a中的电势也会下降。为什么电势会下降呢?
因为a中的空穴太多,就会扩散到b中。
本来a和b都是平衡的,但这个时候b那一侧因为扩散而有了更多的空穴,于是带了正电。
这个时候如果我再把正电荷从半导体a搬运到半导体b,则需要克服这部分正电荷产生的电场力。
电势差这不就产生了吗。
同样我们也可以知道,当半导体a掺入越多的受主杂质,除了电离产生的空穴越来越多,其费米能级
E
F
E_F
EF也会越接近价带,并越偏离本征费米能级
E
i
E_i
Ei。
此可以通过半导体a的
(
E
i
−
E
F
)
(E_i-E_F)
(Ei−EF)间接算出半导体a这一侧的电势
ψ
p
\psi_p
ψp。
往a中掺入受主杂质还不够,我还往半导体b中掺入施主杂质,使b中充满了电离产生的自由电子。
那么,同理也会使半导体b的电势
ψ
n
\psi_n
ψn上升。
用同样的方法算出b侧的电势,两者相减不就得到了两块半导体之间的内间电势(差)了吗?
总结得到:两块半导体中,越掺入释放空穴的杂质则电势越低;越掺入释放电子的杂质则电势越高。
其他科学家已经帮我们把
(
E
i
−
E
F
)
(E_i-E_F)
(Ei−EF)和
ψ
n
和
ψ
p
\psi_n和\psi_p
ψn和ψp的关系式求好了,我们拿来用就行:
ψ
p
=
−
p
q
(
E
i
−
E
F
)
\psi_p=-\frac{p}{q}(E_i-E_F)
ψp=−qp(Ei−EF)
心动不如行动,我们这就立刻开始进行求解。
内建电势 V b i V_{bi} Vbi的推导过程
1.我们先列出包含
(
E
i
−
E
F
)
(E_i-E_F)
(Ei−EF)的表达式,恰巧我知道一个,就是p区和n区各自多子的浓度表达式:
p
区多子浓度
p
=
n
i
e
x
p
(
E
i
−
E
F
k
T
)
p区多子浓度p=n_iexp(\frac{E_i-E_F}{kT})
p区多子浓度p=niexp(kTEi−EF)
p区和n区的少子浓度,我们先假设为0
对p区的多子浓度表达式进行换算,得到: E i − E F = k T l n p n i E_i-E_F=kTln\frac{p}{n_i} Ei−EF=kTlnnip
我们来分析一下上面这个式子中。
kT是温度,室温下为300K(以开);本征载流子浓度
n
i
=
9.65
×
1
0
9
c
m
−
3
n_i=9.65\times 10^{9} cm^{-3}
ni=9.65×109cm−3
你问我
n
i
n_i
ni怎么来的?我带你回顾一下《半导体器件与物理篇1 热平衡时能带和载流子浓度》中的表格吧:
同时一些室温下(300K)重要的常数需要牢记:
| 普朗克常量 h = 6.63 ⋅ 1 0 − 34 J ⋅ s h=6.63\cdot 10^{-34} J\cdot s h=6.63⋅10−34J⋅s | - |
|---|---|
| Si | N c = 2.86 × 1 0 19 c m − 3 N_c=2.86\times 10^{19} cm^{-3} Nc=2.86×1019cm−3 |
| - | N v = 2.66 × 1 0 19 c m − 3 N_v=2.66\times 10^{19} cm^{-3} Nv=2.66×1019cm−3 |
| - | n i = 9.65 × 1 0 9 c m − 3 n_i=9.65\times 10^{9} cm^{-3} ni=9.65×109cm−3 |
| GaAs | N c = 4.7 × 1 0 17 c m − 3 N_c=4.7\times 10^{17} cm^{-3} Nc=4.7×1017cm−3 |
| - | N v = 7.0 × 1 0 18 c m − 3 N_v=7.0\times 10^{18} cm^{-3} Nv=7.0×1018cm−3 |
| - | n i = 2.25 × 1 0 6 c m − 3 n_i=2.25\times 10^{6} cm^{-3} ni=2.25×106cm−3 |
那有哪些变量是未知的呢?
载流子浓度
p
p
p呀!!!
所以第二步,我们就要把这不好直接看出来的这个载流子浓度
p
p
p,转变成我们可以看出来的变量。
比如说,我们对这块半导体掺入了多少杂质(
N
A
和
N
D
N_A和N_D
NA和ND)
2.于是,让我们翻找一下,有哪个公式既包含了载流子浓度,有包含了
N
A
和
N
D
N_A和N_D
NA和ND呢?
已知泊松方程式:
d
2
ψ
d
x
2
=
d
E
d
x
=
ρ
s
ε
s
=
q
(
p
−
n
+
N
D
+
−
N
A
−
)
ε
s
\frac{d^2\psi}{dx^2}=\frac{dE}{dx}=\frac{\rho_s}{\varepsilon_s}=\frac{q(p-n+N_D^{+}-N_A^{-})}{\varepsilon_s}
dx2d2ψ=dxdE=εsρs=εsq(p−n+ND+−NA−)
由空间电荷密度 ρ s \rho_s ρs的表达式可以知道,载流子的浓度需要与其对应的提供者——施主和受主杂质浓度相减。因此在正常情况下,在空间电荷密度应该为0
由此可得整个泊松方程式都为0: p − n + N D + − N A − = 0 p-n+N_D^{+}-N_A^{-}=0 p−n+ND+−NA−=0
这样一来,我们就凑齐了计算电势
ψ
p
\psi_p
ψp最后的一块拼图:
{
p
=
N
A
−
n
=
N
D
+
\begin{cases} p=N_A^{-}\\n=N_D^{+}\end{cases}
{p=NA−n=ND+
掺杂浓度
N
A
和
N
D
N_A和N_D
NA和ND右上角的正负号,表示的是电离的杂质。
最后,我们把所有的龙珠集合起来,就得到了: ψ p = − k T q l n N A n i \psi_p=-\frac{kT}{q}ln\frac{N_A}{n_i} ψp=−qkTlnniNA
3.同理,我们可以得到n区的电势: ψ n = − k T q l n N D n i \psi_n=-\frac{kT}{q}ln\frac{N_D}{n_i} ψn=−qkTlnniND
4.将n区和p区的电势相减,就得到了两区之间的电势差,也就是内建电势 V b i V_{bi} Vbi: V b i = ψ n − ψ p = k T q l n N A N D n i 2 V_{bi}=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2} Vbi=ψn−ψp=qkTlnni2NAND
Pn结特性4:空间电荷区
空间电荷区,也称耗尽层abrupt junction,是指在pn结中,由于自由电子的扩散运动和内电场导致的漂移运动,使得p区和n区的交界处产生的一个薄电荷层
耗尽层其实有两部分,分别是过渡区和可动载流子浓度为0的完全耗尽区。一般将过渡区忽略。
这些掺杂离子的空间电荷部分被可动载流子补偿。越过了过渡区域,进入可动载流子浓度为零的完全耗尽区,这个区域称为耗尽区(空间电荷区)。
由于在耗尽区内“可动载流子浓度为0”,可以得到
p
=
n
=
0
p=n=0
p=n=0
将
p
=
n
=
0
p=n=0
p=n=0代入泊松方程式,得到:
d
2
ψ
d
x
2
=
q
ε
s
(
N
A
−
N
D
)
\frac{d^2\psi}{dx^2}=\frac{q}{\varepsilon_s}(N_A-N_D)
dx2d2ψ=εsq(NA−ND)
耗尽区abrupt junction有两种,分别是突变结和线性缓变结。突变结也分为一般的(通用的)突变结和单边突变结
突变结
突变结是浅扩散或低能离子注入形成的pn结。
因此,当题目提及浅扩散或低能离子注入时,则代入突变结的知识点进行计算
假设掺杂的时候都把半导体给掺均匀了。
我们需要求解这一块耗尽区的宽度 W W W,顺便了解一下其内部的电场强度分布。
宽度W与内建电势、掺杂浓度的关系
为了求得宽度W与内建电势、掺杂浓度的关系,我们需要经历如下流程:
1.半导体的总电荷中性要求p侧每单位面积总负电荷必须精确地和n侧每单位面积总正空间电荷相等:
N
A
⋅
x
p
=
N
D
⋅
x
n
N_A\cdot x_p=N_D\cdot x_n
NA⋅xp=ND⋅xn
p侧耗尽层宽度
x
p
x_p
xp,n侧耗尽层宽度
x
n
x_n
xn
由 x p , x n x_p,x_n xp,xn可以得到: 总耗尽层宽度 W = x p + x n 总耗尽层宽度W=x_p+x_n 总耗尽层宽度W=xp+xn
2.由泊松方程式引入两个已知的变量——掺杂浓度:
d
2
ψ
d
x
2
=
q
ε
s
(
N
A
−
N
D
)
\frac{d^2\psi}{dx^2}=\frac{q}{\varepsilon_s}(N_A-N_D)
dx2d2ψ=εsq(NA−ND)
,对上式积分两次,可以得到一个电势差。如果积分的区间合适,可以得到内建电势
V
b
i
V_{bi}
Vbi
3.第一次积分,得到耗尽层内的电场分布情况: E ( x ) = d ψ d x = { q N A ε s ( x + x p ) , − x p < x < 0 q N D ε s ( x − x n ) , 0 < x < x n E(x)=\frac{d\psi}{dx}=\begin{cases}\frac{qN_A}{\varepsilon_s}(x+x_p),-x_p<x<0\\ \frac{qN_D}{\varepsilon_s}(x-x_n),0<x<x_n \end{cases} E(x)=dxdψ={εsqNA(x+xp),−xp<x<0εsqND(x−xn),0<x<xn
绘制电场强度关于x的坐标轴:

由图可以得到电场强度在耗尽区内的最大值: E m = q N A x p ε s = q N D x n ε s E_m=\frac{qN_Ax_p}{\varepsilon_s}=\frac{qN_Dx_n}{\varepsilon_s} Em=εsqNAxp=εsqNDxn
4.第二次积分,可以得到耗尽区的内建电势 V b i V_{bi} Vbi: V b i = − ∫ − x p 0 E ( x ) d x − ∫ 0 x n E ( x ) d x = 1 2 E m W V_{bi}=-\int_{-x_p}^0 E(x)dx-\int_0^{x_n}E(x)dx=\frac{1}{2}E_mW Vbi=−∫−xp0E(x)dx−∫0xnE(x)dx=21EmW
对上式进行换算,可以得到宽度W关于内建电势的表达式: W = 2 V b i E m W=\frac{2V_{bi}}{E_m} W=Em2Vbi
5.
E
m
E_m
Em有两个表达式,分别采用了p侧的受主杂质和n侧的施主杂质。
为例同时使用p侧的受主杂质浓度和n侧的施主杂质浓度,我们对
W
=
2
V
b
i
E
m
W=\frac{2V_{bi}}{E_m}
W=Em2Vbi进行变换:
W
=
2
V
b
i
E
m
⋅
2
V
b
i
E
m
W=\frac{\sqrt{2V_{bi}}}{\sqrt{E_m}} \cdot \frac{\sqrt{2V_{bi}}}{\sqrt{E_m}}
W=Em2Vbi⋅Em2Vbi
将 E m = q N A x p ε s = q N D x n ε s E_m=\frac{qN_Ax_p}{\varepsilon_s}=\frac{qN_Dx_n}{\varepsilon_s} Em=εsqNAxp=εsqNDxn代入上式,得到: W = 2 ε s q ( 1 N D + 1 N A ) V b i = 2 ε s q ( N A + N D N A N D ) V b i W=\sqrt{\frac{2 \varepsilon_s}{q} (\frac{1}{N_D}+\frac{1}{N_A})V_{bi}}=\sqrt{\frac{2\varepsilon_s}{q}(\frac{N_A+N_D}{N_AN_D})V_{bi}} W=q2εs(ND1+NA1)Vbi=q2εs(NANDNA+ND)Vbi
突变结可以继续分类:当一边的掺杂浓度远大于另一边时,形成单边突变结
单边突变结
单边突变结的定义:p-n结一侧的掺杂浓度与那笔另一侧高的突变结
单边突变结的特点(如
p
+
−
n
p^+ -n
p+−n结指p侧掺杂浓度远高于n侧的单边突变结):
N
A
>
>
N
D
=
=
>
x
p
<
<
x
n
N_A>>N_D==>x_p<<x_n
NA>>ND==>xp<<xn
已知上一章的公式:
W
=
2
ε
s
q
(
1
N
D
+
1
N
A
)
V
b
i
=
2
ε
s
q
(
N
A
+
N
D
N
A
N
D
)
V
b
i
W=\sqrt{\frac{2 \varepsilon_s}{q} (\frac{1}{N_D}+\frac{1}{N_A})V_{bi}}=\sqrt{\frac{2\varepsilon_s}{q}(\frac{N_A+N_D}{N_AN_D})V_{bi}}
W=q2εs(ND1+NA1)Vbi=q2εs(NANDNA+ND)Vbi
由单边突变结
1
N
A
<
<
1
N
D
\frac{1}{N_A}<<\frac{1}{N_D}
NA1<<ND1,我们将
1
N
A
\frac{1}{N_A}
NA1忽略,得到:
W
=
2
ε
s
V
b
i
q
N
D
W=\sqrt{\frac{2\varepsilon_s V_{bi}}{qN_D}}
W=qND2εsVbi
综上所述,决定耗尽区宽度的是掺杂浓度低的区域的浓度
N
D
N_D
ND。
正是由于单边突变结中低掺杂浓度区的浓度直接决定了耗尽区(也就是结内)的性质,因此在PN结这一章里,我们定义
N
B
=
低掺杂浓度区的载流子浓度
N_B=低掺杂浓度区的载流子浓度
NB=低掺杂浓度区的载流子浓度。
因此根据 x p < < x n x_p<<x_n xp<<xn可以得到: W = x n = 2 ε s V b i q N B W=x_n=\sqrt{\frac{2\varepsilon_s V_{bi}}{qN_B}} W=xn=qNB2εsVbi
已知在一般的突变结中最大的电场强度为: E m = q N A x p ε s = q N D x n ε s E_m=\frac{qN_Ax_p}{\varepsilon_s}=\frac{qN_Dx_n}{\varepsilon_s} Em=εsqNAxp=εsqNDxn
将 N B N_B NB代入,得到 E m = q N B W ε s E_m=\frac{qN_BW}{\varepsilon_s} Em=εsqNBW
由此在计算在耗尽区任一点上电场强度: E ( x ) = − E m + q N B x ε s = q N B ε s ( − W + x ) E(x)=-E_m+\frac{qN_Bx}{\varepsilon_s}=\frac{qN_B}{\varepsilon_s}(-W+x) E(x)=−Em+εsqNBx=εsqNB(−W+x)
已知在距离x上对电场进行积分,可以得到耗尽层内电势大小的表达式。进行一次积分后,得到: ψ ( x ) = − q N B 2 ε s x 2 + q N B W ε s x \psi(x)=-\frac{qN_B}{2\varepsilon_s}x^2+\frac{qN_BW}{\varepsilon_s}x ψ(x)=−2εsqNBx2+εsqNBWx
利用宽度W关于内建电势的表达式 W = 2 V b i E m W=\frac{2V_{bi}}{E_m} W=Em2Vbi,可以得到电势大小 ψ ( x ) \psi(x) ψ(x)关于内建电势 V b i V_{bi} Vbi和宽度W的表达式: ψ ( x ) = V b i x W ( 2 − x W ) \psi(x)=\frac{V_{bi}x}{W}(2-\frac{x}{W}) ψ(x)=WVbix(2−Wx)
热平衡下的耗尽层加偏压
对于一个热平衡状态的金属、半导体,我们将对其施加一个可正可负的电压。当我们不知道电压的正负时,我们使用V表示外加偏压;当已知为正向偏压时,我们使用 V F V_F VF,F表示forward;当已知负向偏压时,我们使用 V R V_R VR,R表示reverse。
热平衡下的耗尽层加正向偏压会变薄加反向平压会变厚
耗尽层电压变化
V
R
V_R
VR得到的耗尽层宽度:
W
=
2
ε
s
(
V
b
i
−
V
)
q
N
B
W=\sqrt{\frac{2\varepsilon_s(V_{bi}- V)}{qN_B}}
W=qNB2εs(Vbi−V)
其中
N
B
N_B
NB是轻掺杂的基体浓度,对于正向偏压,V是正值;对于负向偏压,V是负值。
线性缓变结linearly graded junction
线性缓变结的定义:深扩散或高能离子注入产生的,掺杂浓度分布在结区呈线性变化的pn结。
因此,当题目提及深扩散或高能离子注入式,则代入线性缓变结的知识点进行计算。
由于掺杂浓度呈线性分布,假设在 − W 2 < x < W 2 -\frac{W}{2}<x<\frac{W}{2} −2W<x<2W这个耗尽层内部,可以得到其对应的泊松方程式为: d 2 ψ d x 2 = d E d x = − ρ s ε s = − q a x ε s ( − W 2 < x < W 2 ) \frac{d^2\psi}{dx^2}=\frac{dE}{dx}=-\frac{\rho_s}{\varepsilon_s}=\frac{-qax}{\varepsilon_s} (-\frac{W}{2}<x<\frac{W}{2}) dx2d2ψ=dxdE=−εsρs=εs−qax(−2W<x<2W)
对 d E d x = − q a x ε s \frac{dE}{dx}=\frac{-qax}{\varepsilon_s} dxdE=εs−qax进行一次积分,得到电场强度分布: E ( x ) = − q a ε s [ ( W 2 ) 2 − x 2 2 ] E(x)=-\frac{qa}{\varepsilon_s}[\frac{(\frac{W}{2})^2-x^2}{2}] E(x)=−εsqa[2(2W)2−x2]
由电场强度分布的表达式,可以求得电场强度的最大值为: E m = E ( 0 ) = − q a W 2 8 ε s E_m=E(0)=-\frac{qaW^2}{8\varepsilon_s} Em=E(0)=−8εsqaW2
对泊松方程式进行第二次积分,得到电势的分布表达式: ψ ( x ) = − q a ε s [ W 2 8 x − 1 6 x 3 ] \psi(x)=-\frac{qa}{\varepsilon_s}[\frac{W^2}{8}x-\frac{1}{6}x^3] ψ(x)=−εsqa[8W2x−61x3]
由于内建电势为耗尽层两端的电势差,可以得到: V b i = ψ ( x n ) − ψ ( − x p ) = ψ ( W 2 ) − ψ ( − W 2 ) = q a W 3 12 ε s V_{bi}=\psi(x_n)-\psi(-x_p)=\psi(\frac{W}{2})-\psi(-\frac{W}{2})=\frac{qaW^3}{12\varepsilon_s} Vbi=ψ(xn)−ψ(−xp)=ψ(2W)−ψ(−2W)=12εsqaW3
往往内建电势 V b i V_{bi} Vbi是可测的,所以我们要把上式 V b i V_{bi} Vbi关于W的表达式,换算为W关于 V b i V_{bi} Vbi的表达式: W = ( 12 ε s V b i q a ) 1 3 W=(\frac{12\varepsilon_sV_{bi}}{qa})^{\frac{1}{3}} W=(qa12εsVbi)31
因为在耗尽区边缘(-W/2和W/2)的杂质浓度一样,且都等于 a W 2 \frac{aW}{2} 2aW,即 N A = N D = w W 2 N_A=N_D=\frac{wW}{2} NA=ND=2wW所以根据 V b i = ψ ( x n ) − ψ ( − x p ) = k T q l n ( N A N D n i 2 ) V_{bi}=\psi(x_n)-\psi(-x_p)=\frac{kT}{q} ln(\frac{N_AN_D}{n_i^2}) Vbi=ψ(xn)−ψ(−xp)=qkTln(ni2NAND),可以得到线性缓变结的内建电势: V b i = 2 k T q l n ( a W 2 n i ) V_{bi}=\frac{2kT}{q} ln(\frac{aW}{2n_i}) Vbi=q2kTln(2niaW)
势垒电容 C j C_j Cj
单位面积势耗尽层势垒电容 C j C_j Cj的定量表达式为: C j = d Q d V C_j=\frac{dQ}{dV} Cj=dVdQ
d Q dQ dQ是外加偏压变化 d V dV dV时单位面积耗尽层的电荷增量。
再由 d V = W ⋅ d E = W ⋅ d Q ε s dV=W\cdot dE=W\cdot \frac{dQ}{\varepsilon_s} dV=W⋅dE=W⋅εsdQ得到势垒电容的等效表达式为: C j = d Q d V = d Q W d E = d Q W d Q ε s = ε s W C_j=\frac{dQ}{dV}=\frac{dQ}{WdE}=\frac{dQ}{W\frac{dQ}{\varepsilon_s}}=\frac{\varepsilon_s}{W} Cj=dVdQ=WdEdQ=WεsdQdQ=Wεs
由 ε s W \frac{\varepsilon_s}{W} Wεs可以发现,这个表达式和一个普通电容根据介电常数和极板宽度求取电容大小的公式十分类似。
总结势垒电容的变化规律,耗尽层越宽,势垒电容越小。即外加反偏压,势垒电容减压。
扩散电容 C D C_D CD
在推导上式时,只有在耗尽区变化的空间电荷对电容值有贡献,这对反向偏压的情况当然是很好的假设;然而对正向偏压而言,大量电流可以流过结,因此也代表中性区有大量的移动裁流子,这些随着偏压增加的移动载流子增量会贡献出额外的一项电容,称为扩散电容。
扩散电容的定义:耗尽层正向偏压时,随偏压增加的移动载流子增加。这部分增加的移动载流子增量会贡献额外的电容,叫扩散电容。
单边突变结的势垒电容-电压特性曲线
如何推导C与电压V的关系式:
已知:
{
W
=
w
ε
s
(
V
b
i
−
V
)
q
N
B
C
=
ε
s
W
\begin{cases} W=\sqrt{\frac{w \varepsilon_s(V_{bi}-V)}{qN_B}}\\ C=\frac{\varepsilon_s}{W}\end{cases}
{W=qNBwεs(Vbi−V)C=Wεs
两式相结合得到:
C
=
q
ε
s
N
)
B
2
(
V
b
i
−
V
)
C=\sqrt{\frac{q\varepsilon_sN)B}{2(V_{bi}-V)}}
C=2(Vbi−V)qεsN)B
为了方便绘图,我们需要得到一个由C组成的式子关于V的关系式。
聪明的前人已经帮我们推好了,我们来看结果吧:
1
C
2
=
2
(
V
b
i
−
V
)
q
ε
s
N
B
\frac{1}{C^2}=\frac{2(V_{bi}-V)}{q\varepsilon_sN_B}
C21=qεsNB2(Vbi−V)
测量杂质分布的C-V法
这一小节我们用电容电压特性计算杂质分布。
电压增加dV时,耗尽层宽度变宽dW。变宽的这部分所包含的杂质浓度定义为N(w).
对于突变结来说,由(耗尽层类似电容的特性)电容-电压特性可以知道电压增量dV产生了电荷增量dQ
因为电荷是由一个个杂质电离而成的,所以得到电荷和杂质浓度关于电压增量dV和耗尽层宽度增量dW的关系:
d
Q
=
q
N
(
w
)
d
w
dQ=qN(w)dw
dQ=qN(w)dw
N
(
w
)
d
w
N(w)dw
N(w)dw为宽度dW下杂质的数量
电场增加dE,并不是只在边缘区域dW这里增加一点点电场,而是牵一发而动全身,让耗尽层整个宽度的电场都增加了。并且,我们可以大致上认为这个电场强度在耗尽区的任何地方都增加了dE。
由
V
=
W
⋅
E
V=W\cdot E
V=W⋅E和
V
n
e
w
=
(
W
+
d
W
)
⋅
(
E
+
d
E
)
V_{new}=(W+dW)\cdot (E+dE)
Vnew=(W+dW)⋅(E+dE),并且把dW忽略掉,我们可以得到:
d
V
≈
W
⋅
d
E
dV\approx W\cdot dE
dV≈W⋅dE
将
E
=
Q
ε
s
E=\frac{Q}{\varepsilon_s}
E=εsQ 和
d
Q
=
q
N
(
w
)
d
w
dQ=qN(w)dw
dQ=qN(w)dw代入,得到:
d
V
≈
W
d
Q
ε
s
=
q
N
(
W
)
⋅
W
d
W
ε
s
dV\approx \frac{WdQ}{\varepsilon_s}=\frac{qN(W)\cdot WdW}{\varepsilon_s}
dV≈εsWdQ=εsqN(W)⋅WdW
可以看到 W d W WdW WdW中的宽度W分布在微分的内外,这有点不好看。于是,我们运用简单的微积分,得到: d V ≈ W d Q ε s = q N ( W ) ⋅ d ( W 2 ) 2 ε s dV\approx \frac{WdQ}{\varepsilon_s}=\frac{qN(W)\cdot d(W^2)}{2\varepsilon_s} dV≈εsWdQ=2εsqN(W)⋅d(W2)
将 C j = ε s W C_j=\frac{\varepsilon_s}{W} Cj=Wεs代入,并将N(W)提取出来,得到: N ( W ) = 2 q ε s [ 1 d ( 1 / C j 2 ) d V ] N(W)=\frac{2}{q\varepsilon_s}[\frac{1}{\frac{d(1/C_j^2)}{dV}}] N(W)=qεs2[dVd(1/Cj2)1]
这个式子就好用多了。因为每单位面积的电容值和反向偏压(因为要让耗尽区增宽)的大小我们是能很容易测得的。然后我们再作图得到 q / C j 2 q/C_j^2 q/Cj2和dV的关系,就能轻松得到增加的载流子浓度N(W)了
以上就是对于突变结,尤其是单边突变结的**测量杂志分布的C-V法了。
对于线性缓变结,则同理,可以由斜率和交点得到杂质梯度a和内建电势
V
b
i
V_{bi}
Vbi
W
=
(
12
ε
s
B
b
i
q
a
)
1
/
3
W=(\frac{12\varepsilon_sB_{bi}}{qa})^{1/3}
W=(qa12εsBbi)1/3
C
j
=
ε
s
W
=
[
q
a
ε
s
2
12
(
V
b
i
−
V
)
]
1
/
3
F
/
c
m
2
C_j=\frac{\varepsilon_s}{W}=[\frac{qa\varepsilon_s^2}{12(V_{bi}-V)}]^{1/3} F/cm^2
Cj=Wεs=[12(Vbi−V)qaεs2]1/3F/cm2
杂志梯度a。
变容器varactor
变容器(也称为可变电容器)的定义:利用反向偏压时电压可调特性的pn结器件。
首先对反向偏压的势垒电容进行一个定性的描述:
C
j
∝
(
V
b
i
+
V
R
)
−
n
C_j\propto (V_{bi}+V_R)^{-n}
Cj∝(Vbi+VR)−n
对于线性缓变结,其
n
=
1
3
n=\frac{1}{3}
n=31
对于突变结,其
n
=
1
2
n=\frac{1}{2}
n=21
由线性缓变结的电容与反向偏压关系式
C
j
=
[
q
a
ε
s
2
12
(
V
b
i
−
V
)
]
1
3
C_j=[\frac{qa\varepsilon_s^2}{12(V_{bi}-V)}]^{\frac{1}{3}}
Cj=[12(Vbi−V)qaεs2]31,和单边突变结的电容与反向偏压关系式
1
C
2
=
2
(
V
b
i
−
V
)
q
ε
s
N
B
\frac{1}{C^2}=\frac{2(V_{bi}-V)}{q\varepsilon_sN_B}
C21=qεsNB2(Vbi−V),我们可以得到:反向偏压越大,势垒电容越大。
这条结论的数学表达式为:
C
j
∝
(
V
R
)
−
n
,
V
R
>
>
V
b
i
C_j \propto(V_R)^{-n},V_R>>V_{bi}
Cj∝(VR)−n,VR>>Vbi
 由图可得,p±n的掺杂分布,其施主分布
N
D
(
x
)
N_D(x)
ND(x)可表示为
B
(
x
/
x
0
)
m
B(x/x_0)^m
B(x/x0)m,其中B和
x
0
x_0
x0是常数,而对线性缓变结m=1,对突变结m=0,对超突变结m=-3/2
由图可得,p±n的掺杂分布,其施主分布
N
D
(
x
)
N_D(x)
ND(x)可表示为
B
(
x
/
x
0
)
m
B(x/x_0)^m
B(x/x0)m,其中B和
x
0
x_0
x0是常数,而对线性缓变结m=1,对突变结m=0,对超突变结m=-3/2
##变容器的电流电压特性
当在p-n结外加一电压,将会打乱电子和空穴的扩散及漂移电流间的平衡。

如图所示,在正向偏压时,外加的偏压降低跨过耗尽区的静电电势。与扩散电流相比,漂移电流降低了。由p端到n端的空穴扩散电流和n端到p端的电子扩散电流增加了。因此,少数载流子注入的现象发生,亦即电子注入p端,而空穴注入n端.

在反向偏压下,外加的电压增加了跨过耗尽区的静电电势,如中间图所示。如此将大大地减少扩散电流,导致一小的反向电流.
理想电流-电压特性
这一小节我们要求理想pn结的电流(主要是电流密度)和电压的关系
首先,什么是理想pn结需要假设满足的条件?
条件包括:
①耗尽区为突变边界,且假设在边界之外,半导体为电中性;
②边界处的载流子浓度与跨过结的静电电势有关;
③小注入情况,亦即注入的少数载流子浓度远小于多数载流子浓度;
④耗尽区内无产生和复合电流,且电子和空穴在耗尽区内为常数。
由第2条假设“②边界处的载流子浓度与跨过结的静电电势有关”,于是我们用掺杂浓度 N A , N D N_A,N_D NA,ND表示内建电势 V b i V_{bi} Vbi为: V b i = ψ n − ψ p = k T q l n ( N A N D n i 2 ) V_{bi}=\psi_n-\psi_p=\frac{kT}{q} ln(\frac{N_AN_D}{n_i^2}) Vbi=ψn−ψp=qkTln(ni2NAND)
由于在热平衡时,中性区的多数载流子浓度与杂质浓度基本相等,也就是
n
n
0
=
N
A
,
p
p
0
=
N
D
n_{n0}=N_A,p_{p0}=N_D
nn0=NA,pp0=ND,故可得
V
b
i
=
ψ
n
−
ψ
p
=
k
T
q
l
n
(
n
n
0
p
p
0
n
i
2
)
V_{bi}=\psi_n-\psi_p=\frac{kT}{q} ln(\frac{n_{n0}p_{p0}}{n_i^2})
Vbi=ψn−ψp=qkTln(ni2nn0pp0)
n
n
0
n_{n0}
nn0和
n
p
0
n_{p0}
np0分别表示为在n和p侧的平衡电子浓度,下标0表示热平衡。
由于 p p 0 ⋅ n n 0 = n i 2 p_{p0}\cdot n_{n0}=n_i^2 pp0⋅nn0=ni2,可以进一步推导得: V b i = k T q l n ( n n 0 n p 0 ) V_{bi}=\frac{kT}{q} ln(\frac{n_{n0}}{n_{p0}}) Vbi=qkTln(np0nn0)
将上式换算,可以得到n侧与p侧的电子浓度关系: n n 0 = n p 0 ⋅ e q V b i k T n_{n0}=n_{p0}\cdot e^{\frac{qV_{bi}}{kT}} nn0=np0⋅ekTqVbi
同理可得n侧与怕p侧的空穴浓度关系: p p 0 = p n 0 ⋅ e q V b i k T p_{p0}=p_{n0}\cdot e^{\frac{qV_{bi}}{kT}} pp0=pn0⋅ekTqVbi
当不再保持热平衡,而是施加了外在电压 V V V时,得到: { n n = n p ⋅ e x p ( q ( V b i − V ) k T ) p p = p n ⋅ e x p ( q ( V b i − V ) k T ) \begin{cases} n_n=np\cdot exp({\frac{q(V_{bi}-V)}{kT}}) \\ p_p=p_n \cdot exp(\frac{q(V_{bi}-V)}{kT}) \end{cases} {nn=np⋅exp(kTq(Vbi−V))pp=pn⋅exp(kTq(Vbi−V))
由于小注入时,注入的少数载流子浓度比多数载流子少。因此满足: n n ≈ n n 0 n_n\approx n_{n0} nn≈nn0且 n n 0 = n p 0 e x p ( q V b i k T ) n_{n0}=n_{p0}exp(\frac{qV_{bi}}{kT}) nn0=np0exp(kTqVbi)
将上面两式代入n区的多子与少子关系 n n = n p ⋅ e x p ( q ( V b i − V ) k T ) n_n=np\cdot exp({\frac{q(V_{bi}-V)}{kT}}) nn=np⋅exp(kTq(Vbi−V)),得到: n n = n n 0 = n p 0 e x p ( q V b i k T ) = n p 0 e x p ( q V b i k T ) ≈ n p e x p [ q ( V b i − V ) k T ] n_n=n_{n0}=n_{p0}exp(\frac{qV_{bi}}{kT})=n_{p0} exp(\frac{qV_{bi}}{kT} )\approx n_p exp[\frac{q(V_{bi}-V)}{kT}] nn=nn0=np0exp(kTqVbi)=np0exp(kTqVbi)≈npexp[kTq(Vbi−V)]
等式两边将内建电视 V b i V_{bi} Vbi约去得到: n p = n p 0 ⋅ e x p ( q V k T ) n_p=n_{p0} \cdot exp(\frac{qV}{kT}) np=np0⋅exp(kTqV),即: n p − n p 0 = n p 0 ⋅ [ e x p ( q V k T ) − 1 ] n_p-n_{p0}=n_{p0} \cdot [exp(\frac{qV}{kT})-1] np−np0=np0⋅[exp(kTqV)−1]
同理可得
p
n
=
p
n
0
e
x
p
(
q
V
k
T
)
p_n=p_{n0}exp(\frac{qV}{kT})
pn=pn0exp(kTqV)或
p
n
−
p
n
0
=
p
n
0
(
e
x
p
(
q
V
k
T
−
1
)
p_n-p_{n0}=p_{n0}(exp(\frac{qV}{kT}-1)
pn−pn0=pn0(exp(kTqV−1)
可见,在正向偏压下,边界
−
x
p
-x_p
−xp和
x
n
x_n
xn的少数载流子浓度实际上比平衡时要大;但在反向偏压下,少数载流子浓度比平衡时要小。
已由于第4条假设“④耗尽区内无产生和复合电流,且电子和空穴在耗尽区内为常数”,所以我们简化稳态连续性方程式,得到: d 2 p n d x 2 − p n − p n 0 D p τ p = 0 \frac{d^2p_n}{dx^2}-\frac{p_n-p_{n0}}{D_p\tau_p}=0 dx2d2pn−Dpτppn−pn0=0
令 y = p n − p n 0 y=p_n-p_{n0} y=pn−pn0,得到: d 2 y d x 2 − y L p 2 = 0 \frac{d^2y}{dx^2}-\frac{y}{L_p^2}=0 dx2d2y−Lp2y=0
其中,扩散长度 L p = D p τ p L_p=\sqrt{D_p\tau_p} Lp=Dpτp
因为连续性方程式的边界条件满足:
{
p
n
=
p
n
0
e
x
p
(
q
V
k
T
)
p
n
(
x
=
∝
)
=
p
n
0
\begin{cases} p_n=p_{n0}exp(\frac{qV}{kT}) \\p_n(x=\propto)=p_{n0} \end{cases}
{pn=pn0exp(kTqV)pn(x=∝)=pn0
所以求解上面这个二阶微分方程,得到:
y
=
p
n
−
p
n
0
=
p
n
0
[
e
x
p
(
q
V
k
T
−
1
)
]
e
x
p
[
−
(
x
−
x
m
)
L
p
]
y=p_n-p_{n0}=p_{n0}[exp(\frac{qV}{kT}-1)]exp[\frac{-(x-x_m)}{L_p}]
y=pn−pn0=pn0[exp(kTqV−1)]exp[Lp−(x−xm)]
上面所有的步骤,都是为了求得关于p区或n区少数载流子浓度的表达式。
由少数载流子的浓度表达式,我们可以进一步推算电流密度。
由于第4条假设“④耗尽区内无产生和复合电流,且电子和空穴在耗尽区内为常数”,并且周围没有施加磁场(也就没有漂移运动)。
于是我们可以知道,此时的电流密度全部由扩散作用引起。
于是我们直接得到在 x = x n x=x_n x=xn处与 x = − x p x=-x_p x=−xp处的扩散电流密度为: { J p ( x n ) = − q D p d p n d x ∣ x n = q D p p n 0 L p [ e x p ( q V k T − 1 ) ] J n ( − x p ) = q D n d n p d x ∣ − x p = q D p n p 0 L n [ e x p ( q V k T − 1 ) ] \begin{cases} J_p(x_n)=-qD_p\frac{dp_n}{dx}|_{x_n}=\frac{qD_pp_{n0}}{L_p}[exp(\frac{qV}{kT}-1)] \\ J_n(-x_p)=qD_n\frac{dn_p}{dx}|_{-x_p}=\frac{qD_pn_{p0}}{L_n}[exp(\frac{qV}{kT}-1)] \end{cases} {Jp(xn)=−qDpdxdpn∣xn=LpqDppn0[exp(kTqV−1)]Jn(−xp)=qDndxdnp∣−xp=LnqDpnp0[exp(kTqV−1)]
在n区,空穴扩散电流以扩散长度 L p L_p Lp呈指数规律衰减;而在p区,电子扩散电流以扩散长度 L n L_n Ln呈指数规律衰减。
最终得到理想二极管方程式,也就是理想pn结扩散电流密度的方程式为: J = J p ( x n ) + J n ( − x p ) = J s [ e x p ( q V k T ) − 1 ] J=J_p(x_n)+J_n(-x_p)=J_s[exp(\frac{qV}{kT})-1] J=Jp(xn)+Jn(−xp)=Js[exp(kTqV)−1]
其中, J s J_s Js是饱和电流密度,其大小为: J s = q D p p n 0 L p + q D n n p 0 L n J_s=\frac{qD_pp_{n0}}{L_p}+\frac{qD_nn_{p0}}{L_n} Js=LpqDppn0+LnqDnnp0
可以看出,总的电流密度可以用p区和n区各自的少子浓度与扩散系数、扩散长度表示。
产生-复合和大注入影响
讨论过小注入后,我们接下来讨论另一种情况——大注入。
大注入情况下,在耗尽区的产生电流为:
J
g
e
n
=
q
n
i
W
τ
g
J_{gen}=\frac{qn_iW}{\tau_g}
Jgen=τgqniW
产生寿命
τ
g
\tau_g
τg;
对于 n i n_i ni较大的半导体,如锗,在室温下扩散电流占优势,反向电流符合理想二极管方程式 J = J s [ e x p ( q V k T ) − 1 ] J=J_s[exp(\frac{qV}{kT})-1] J=Js[exp(kTqV)−1];但是如果 n i n_i ni很小,如硅和砷化镓,则耗尽区的产生电流占优势,应该使用本小节的公式 J g e n = q n i W τ g J_{gen}=\frac{qn_iW}{\tau_g} Jgen=τgqniW。
大注入下的电流-电压特性
正向电流密度
不论是复合还是产生,最有效的中心皆位于接近E的地方
复合电流 J r e c J_{rec} Jrec,有效复合寿命 τ r \tau_r τr。总正向电流 J J J或 J F J_F JF
一般总正向电流表达式为:KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: …ac{qV}{\eta kT)
其中
η
\eta
η称为理想系数。当理想扩散电流占优势时,n等于1;当复合电流占优势时,n等于2;当两者电流相差不多时,n介于1和2之间。

上图显示室温下硅和砷化镓p-n结测量的正向特性。在低电流区域,复合电流占优势, η \eta η等于2;在较高的电流区域,扩散电流占优势, η \eta η接近1。
电流大小
在大注入情况下,电流增加率较缓慢。
工作温度对硅二极管的正向偏压特性有巨大影响。在室温且在小的正向偏压下,复合电流占优势;然而在较高的正向偏压时,扩散电流占优势。给定一正向偏压,随着温度的增加,扩散电流增加速率较复合电流快。
#电荷存储和暂态响应
在正向偏压下,电子由n区被注入到p区,而空穴由p区被注入到n区,少数载流子一旦越过结注入,就和多数载流子复合,且随距离呈指数式衰退,如图所示,这些少数载流子的分布导致在p-n结上电流流动及电荷储存。

被注入的少数载流子存储在中性n区,其每单位面积电荷的计算式:
Q
p
=
q
L
p
p
n
0
[
e
x
p
(
q
V
k
T
−
1
]
Q_p=qL_pp_{n0}[exp(\frac{qV}{kT}-1]
Qp=qLppn0[exp(kTqV−1]
已知在n区pn结的边界处少子扩散电流密度为:
J
p
(
x
n
)
=
q
D
p
p
n
0
L
p
[
e
x
p
(
q
V
k
T
−
1
]
J_p(x_n)=\frac{qD_pp_{n0}}{L_p}[exp(\frac{qV}{kT}-1]
Jp(xn)=LpqDppn0[exp(kTqV−1]
结合得到:
Q
p
=
L
p
2
D
p
J
p
(
x
n
)
=
τ
p
J
p
(
x
n
)
Q_p=\frac{L_p^2}{D_p}J_p(x_n)=\tau_pJ_p(x_n)
Qp=DpLp2Jp(xn)=τpJp(xn)。该式说明电荷储存量是电流和少数载流子寿命的乘积。这是因为若注入的空穴寿命较长,则在被复合之前,会更深地扩散入n区,因而可储存较多的空穴。
扩散电容
当结处于反向偏压时,耗尽层势垒电容为主要的结电容;
当结处于正向偏压时,中性区储存电荷的重新排列,对结电容会产生显著的附加电容,这称为扩散电容,标示为
C
d
C_d
Cd。
定义扩散电容:
C
d
=
A
d
Q
p
d
V
C_d=\frac{AdQ_p}{dV}
Cd=dVAdQp
将
Q
p
=
q
L
p
p
n
0
[
e
x
p
(
q
V
k
T
−
1
)
]
Q_p=qL_pp_{n0}[exp(\frac{qV}{kT}-1)]
Qp=qLppn0[exp(kTqV−1)]代入,得到:
C
d
=
A
q
2
L
p
p
n
0
e
x
p
(
q
V
k
T
)
C_d=\frac{Aq^2L_pp_{n0}}exp(\frac{qV}{kT})
Cd=eAq2Lppn0xp(kTqV)
器件横截面积A;

电导G;总势垒电容 C j C_j Cj
暂态响应
p-n结的暂态响应主要是由于其内部电荷的存储和释放过程引起的。
结击穿
当一足够大的反向电压加在p-n结时,结会击穿而导通一非常大的电流.两种重要的击穿机制为隧道效应和雪崩倍增。对大部分的二极管而言,雪崩击穿限制反向偏压的上限,也限制了双极型品体管的集电极电压。
隧道效应
当一反间强电场加在p-n结时,价电子可以由价带移动到导带。这种电子穿过禁带的过程称为隧穿。隧穿只发生在电场很高的时候。
对硅和砷化镓,其典型电场大约为
1
0
6
V
/
c
m
10^6V/cm
106V/cm或更高:为了得到如此高的电场,p区和n区的掺杂浓度必须相当高(
>
5
×
1
0
17
c
m
−
3
>5\times 10^{17}cm^{-3}
>5×1017cm−3)
隧道效应示意图:

雪崩效应
如果电场足够大,电子可以获得足够的动能,以致于当和原子产生撞击时,可以破坏键而产生电子-空穴对。这些新产生的电子和空穴,可由电场获得动能,并产生额外的电子-空穴对。这些过程生生不息,连续产生新的电子-空穴对。这种过程称为雪崩倍增,
对于硅和砷化镓结,击穿电压约小于 4 E g / q 4E_g/q 4Eg/q时,其击穿机制归因于隧道效应;击穿电压超过 6 E g / q 6E_g/q 6Eg/q,其击穿机制归因于雪崩倍增。当电压在 4 E g / q 4E_g/q 4Eg/q和 6 E g / q 6E_g/q 6Eg/q之间,击穿则为雪崩倍增和隧穿二者共同作用的结果
击穿电压
定义临场电场
E
c
E_c
Ec,击穿电压
V
B
V_B
VB
单边突变结的击穿电压表达式:
V
B
=
E
c
W
2
=
ε
s
E
c
2
2
q
N
B
−
1
V_B=\frac{E_cW}{2}=\frac{\varepsilon_sE_c^2}{2q}N_B^{-1}
VB=2EcW=2qεsEc2NB−1
线性缓变结的击穿电压:
V
B
=
2
E
c
W
3
=
4
E
c
3
/
2
3
(
2
ε
s
q
)
1
/
2
α
−
1
/
2
V_B=\frac{2E_cW}{3}=\frac{4E_c^{3/2}}{3}(\frac{2\varepsilon_s}{q})^{1/2}\alpha^{-1/2}
VB=32EcW=34Ec3/2(q2εs)1/2α−1/2
轻掺杂侧的浓度
N
B
N_B
NB;半导体介电常数
ε
s
\varepsilon_s
εs;浓度梯度
α
\alpha
α
对于一给定 N B N_B NB或 α \alpha α,砷化镓比硅有较高的击穿电压,主要是因为其有较大的禁带宽度。禁带宽度越大,临界电场就必须越大,才能在碰撞间获得足够的动能。临界电场越大,击穿电压就越大.。
异质结
异质结的定义:用两种不同半导体材料所组成的结。
功函数 q ϕ q\phi qϕ:将一电子由费米能级E移到真空能级所需的能量。
电子亲和力 q x qx qx:将一电子由导带E底部移到真空能级所需的能量。
忽略耗尽区的异质结能带图:
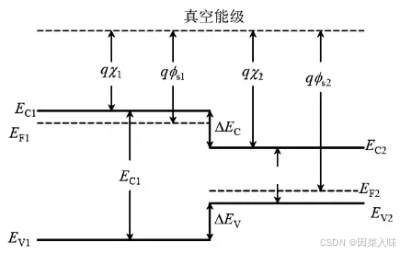
两半导体导带边缘的能量差为
Δ
E
C
\Delta E_C
ΔEC。因为所有半导体的真空能级都是一样的,因此可以用哥导带与真空能级的距离来表示导带的能量差:
Δ
E
C
=
q
x
2
−
q
x
1
\Delta E_C=qx_2-qx_1
ΔEC=qx2−qx1
而价带边缘的能量差表示为
Δ
E
V
\Delta E_V
ΔEV。使用同样的表示思路,可表示为:
E
V
=
E
g
1
+
q
x
1
−
(
E
g
2
+
q
x
2
)
=
Δ
E
g
−
Δ
E
C
E_V=E_{g1}+qx_1-(E_{g2}+qx_2)=\Delta E_g-\Delta E_C
EV=Eg1+qx1−(Eg2+qx2)=ΔEg−ΔEC
禁带宽度差
Δ
E
g
=
E
g
1
−
E
g
2
\Delta E_g=E_{g1}-E_{g2}
ΔEg=Eg1−Eg2
异质结的能带图
构建能带图有两个基本的假设:1.在热平衡下,界面两端的费米能级必须相同;2.真空能级必须连续,且平行于能带边缘。
由于这些假设,只要禁带宽度
E
g
E_g
Eg和电子亲和力
q
x
qx
qx皆非杂质浓度的函数,则导带边缘的不连续
Δ
E
C
\Delta E_C
ΔEC。和价带边缘的不连续
δ
E
V
\delta E_V
δEV不会被杂质浓度影响。
包含异质结的能带图,几乎囊括了所有能带与电势的关系:

总内建电势为:
V
b
i
=
V
b
1
+
V
b
2
V_{bi}=V_{b1}+V_{b2}
Vbi=Vb1+Vb2
在热平衡时,半导体1和2的静电势
V
b
1
V_{b1}
Vb1和
V
b
2
V_{b2}
Vb2
当外加偏压时,半导体1的静电势为: V b 1 = ε 2 N 2 ( V b i − V ) ε 1 N 1 + ε 2 N 2 V_{b1}=\frac{\varepsilon_2N_2(V_{bi}-V)}{\varepsilon_1N_1+\varepsilon_2N_2} Vb1=ε1N1+ε2N2ε2N2(Vbi−V)
当外加偏压时,半导体2的静电势为:
V
b
2
=
ε
1
N
1
(
V
b
i
−
V
)
ε
1
N
1
+
ε
2
N
2
V_{b2}=\frac{\varepsilon_1N_1(V_{bi}-V)}{\varepsilon_1N_1+\varepsilon_2N_2}
Vb2=ε1N1+ε2N2ε1N1(Vbi−V)
单纯就两个静电势的公式来说,有点像电阻的并联分流公式。
由半导体1的静电势 V b 1 V_{b1} Vb1和半导体1的杂质浓度 N 1 N_1 N1,可以得到半导体1的耗尽区宽度为: x 1 = 2 ε 1 ε 2 N 2 ( V b i − V ) 1 N 1 ( ε 1 N 1 + ε 2 N 2 ) x_1=\sqrt{\frac{2\varepsilon_1 \varepsilon_2N_2(V_{bi}-V)}{1N_1(\varepsilon_1N_1+\varepsilon_2N_2)}} x1=1N1(ε1N1+ε2N2)2ε1ε2N2(Vbi−V)
将 V b 1 V_{b1} Vb1的表达式代入,可以得到: x 1 = 2 ε 1 q N 1 V b 1 x_1=\sqrt{\frac{2\varepsilon_1}{qN_1} V_{b1}} x1=qN12ε1Vb1
由半导体1的静电势 V b 2 V_{b2} Vb2和半导体2的杂质浓度 N 2 N_2 N2,可以得到半导体2的耗尽区宽度为: x 2 = 2 ε 1 ε 2 N 2 ( V b i − V ) 1 N 1 ( ε 1 N 1 + ε 2 N 2 ) x_2=\sqrt{\frac{2\varepsilon_1 \varepsilon_2N_2(V_{bi}-V)}{1N_1(\varepsilon_1N_1+\varepsilon_2N_2)}} x2=1N1(ε1N1+ε2N2)2ε1ε2N2(Vbi−V)
将 V b 2 V_{b2} Vb2的表达式代入,可以得到: x 1 = 2 ε 2 q N 2 V b 1 x_1=\sqrt{\frac{2\varepsilon_2}{qN_2} V_{b1}} x1=qN22ε2Vb1
习题
例1:计算一硅p-n结在300K时的内建电势,
N
A
=
1
0
18
c
m
−
3
N_A=10^{18}cm^{-3}
NA=1018cm−3和
N
D
=
1
0
15
c
m
−
3
N_D=10^{15}cm^{-3}
ND=1015cm−3
需要用到的公式包括1.内建电势与pn结掺杂浓度的关系式
V
b
i
=
ψ
n
−
ψ
p
=
k
T
q
l
n
N
A
N
D
n
i
2
V_{bi}=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2}
Vbi=ψn−ψp=qkTlnni2NAND


例2:一硅单边突变结,其
N
A
=
1
0
19
c
m
−
3
N_A=10^{19}cm^{-3}
NA=1019cm−3,
N
D
=
1
0
16
c
m
−
3
N_D=10^{16}cm^{-3}
ND=1016cm−3,计算在零偏压时的耗尽区宽度和最大电场(T=300K)。
需要用到的公式包括1.内建电势与pn结掺杂浓度的关系式 2.单边突变结的耗尽区宽度表达式
W
=
x
n
=
2
ε
s
V
b
i
q
N
B
W=x_n=\sqrt{\frac{2\varepsilon_s V_{bi}}{qN_B}}
W=xn=qNB2εsVbi 3.最大电场的计算式
E
m
=
q
N
B
W
ε
s
E_m=\frac{qN_BW}{\varepsilon_s}
Em=εsqNBW
4.真空介电常数
ε
0
=
8.85
×
1
0
−
12
F
/
m
\varepsilon_0=8.85\times 10^{-12}F/m
ε0=8.85×10−12F/m 5.
硅的
ε
s
=
11.7
ε
0
硅的\varepsilon_s=11.7\varepsilon_0
硅的εs=11.7ε0
(算得可能不正确)

例3:对于一浓度梯度为
1
0
20
c
m
−
4
10^{20}cm^{-4}
1020cm−4的硅线性缓变结,耗尽区宽度为
0.5
μ
m
0.5\mu m
0.5μm。计算最大电场和内建电势(T=300K)
需要用到的公式包括1.线性缓变结的最大电场表达式
E
m
=
E
(
0
)
=
−
q
a
W
2
8
ε
s
E_m=E(0)=-\frac{qaW^2}{8\varepsilon_s}
Em=E(0)=−8εsqaW2 2.线性缓变结的内建电势表达式
V
b
i
=
q
a
W
3
12
ε
s
V_{bi}=\frac{qaW^3}{12\varepsilon_s}
Vbi=12εsqaW3 3.
N
A
=
N
D
=
a
W
2
N_A=N_D=\frac{aW}{2}
NA=ND=2aW

例4:对一硅突变结,其中
N
A
=
2
×
1
0
19
c
m
−
3
,
N
D
=
8
×
1
0
15
c
m
−
3
N_A=2\times10^{19}cm^{-3},N_D=8\times 10^{15}cm^{-3}
NA=2×1019cm−3,ND=8×1015cm−3,计算零偏压和反向偏压4V时的结电容(T=300K)
需要用到的公式包括1.内建电势与pn结掺杂浓度的关系式 2.存在外加偏压时的单边突变结的耗尽区宽度表达式 3.扩散电容表达式
C
d
=
A
q
2
L
p
p
n
0
e
x
p
(
q
V
k
T
)
C_d=\frac{Aq^2L_pp_{n0}}exp(\frac{qV}{kT})
Cd=eAq2Lppn0xp(kTqV)

例5:计算硅p-n结二极管的理想反向饱和电流,其截面积为
A
=
2
×
1
0
−
4
c
m
2
A=2\times10^{-4} cm^2
A=2×10−4cm2。二极管的参数是:
N
A
=
5
×
1
0
16
c
m
3
,
N
D
=
10
×
16
c
m
−
3
,
n
i
=
9.65
×
10
c
m
−
3
,
D
n
=
21
c
m
2
/
s
,
D
p
=
10
c
m
2
/
s
,
τ
p
0
=
τ
n
0
=
5
×
1
0
−
7
s
N_A=5\times 10^{16}cm^3,N_D=10\times {16}cm^{-3},n_i=9.65\times 10cm^{-3},D_n=21cm^2/s ,D_p=10 cm^2/s ,\tau_{p0}=\tau_{n0}=5\times 10^{-7} s
NA=5×1016cm3,ND=10×16cm−3,ni=9.65×10cm−3,Dn=21cm2/s,Dp=10cm2/s,τp0=τn0=5×10−7s。
需要用到的公式包括1.饱和电流密度的计算式
J
s
=
q
D
p
p
n
0
L
p
+
q
D
n
n
p
0
L
n
J_s=\frac{qD_pp_{n0}}{L_p}+\frac{qD_nn_{p0}}{L_n}
Js=LpqDppn0+LnqDnnp0;理想二极管方程式
J
=
J
p
(
x
n
)
+
J
n
(
−
x
p
)
=
J
s
[
e
x
p
(
q
V
k
T
)
−
1
]
J=J_p(x_n)+J_n(-x_p)=J_s[exp(\frac{qV}{kT})-1]
J=Jp(xn)+Jn(−xp)=Js[exp(kTqV)−1] 2.扩散长度的计算式
L
p
=
D
p
τ
p
L_p=\sqrt{D_p\tau_p}
Lp=Dpτp 3.电流与电流密度的关系式
I
S
=
A
J
s
I_S=A J_s
IS=AJs

例6:一硅p-n结二极管的截面积为
2
×
1
0
−
4
c
m
2
2\times 10^{-4}cm^2
2×10−4cm2。二极管的参数是:
N
A
=
5
×
1
0
16
c
m
−
3
N_A=5\times10^{16}cm^{-3}
NA=5×1016cm−3,
N
D
=
1
0
16
c
m
3
N_D=10^{16}cm^3
ND=1016cm3,
n
i
=
9.65
×
1
0
9
c
m
−
3
n_i=9.65\times 10^9cm^{-3}
ni=9.65×109cm−3,
D
n
=
21
c
m
2
/
s
D_n=21 cm^2/s
Dn=21cm2/s,
D
p
=
10
c
m
2
/
s
D_p=10cm^2/s
Dp=10cm2/s,
τ
p
0
=
τ
n
0
=
5
×
1
0
7
s
\tau_{p0}=\tau_{n0}=5\times10^7 s
τp0=τn0=5×107s。假设
τ
g
=
τ
p
=
τ
n
\tau_g=\tau_p=\tau_n
τg=τp=τn,计算在4V的反向偏压时,其产生的电流密度。
需要用到的公式包括1.内建电势与pn结掺杂浓度的关系式 2.耗尽区宽度与内建电势的关系式 3.在大注入情况下在耗尽区的产生电流的计算式
J
g
e
n
=
q
n
i
W
τ
g
J_{gen}=\frac{qn_iW}{\tau_g}
Jgen=τgqniW,产生寿命
τ
g
\tau_g
τg;
(答案不一致)

例7:对于一理想硅p*-n突变结,其
N
D
=
8
×
1
0
15
c
m
−
3
N_D=8\times 10^{15}cm^{-3}
ND=8×1015cm−3。计算当外加1V正向偏压时,储存在中性区少数载流子每单位面积的数目。空穴的扩散长度是
5
μ
m
5\mu m
5μm。
需要用到的公式包括1.在正向偏压下少数载流子越过结注入的每单位面积电荷的计算式
Q
p
=
q
L
p
p
n
0
[
e
x
p
(
q
V
k
T
−
1
]
Q_p=qL_pp_{n0}[exp(\frac{qV}{kT}-1]
Qp=qLppn0[exp(kTqV−1]

例8:计算硅单边p*-n突变结的击穿电压,其
N
D
=
5
×
1
0
16
c
m
−
3
N_D=5\times 10^{16}cm^{-3}
ND=5×1016cm−3

需要用到的公式包括1.单边突变结的击穿电压表达式:
V
B
=
E
c
W
2
=
ε
s
E
c
2
2
q
N
B
−
1
V_B=\frac{E_cW}{2}=\frac{\varepsilon_sE_c^2}{2q}N_B^{-1}
VB=2EcW=2qεsEc2NB−1;线性缓变结的击穿电压:
V
B
=
2
E
c
W
3
=
4
E
c
3
/
2
3
(
2
ε
s
q
)
1
/
2
α
−
1
/
2
V_B=\frac{2E_cW}{3}=\frac{4E_c^{3/2}}{3}(\frac{2\varepsilon_s}{q})^{1/2}\alpha^{-1/2}
VB=32EcW=34Ec3/2(q2εs)1/2α−1/2;轻掺杂侧的浓度
N
B
N_B
NB;半导体介电常数
ε
s
\varepsilon_s
εs;浓度梯度
α
\alpha
α

例9:考虑一理想突变异质结,其内建电势为1. 6V。在半导体1和2的掺杂浓度为施主
1
×
1
0
16
c
m
−
3
1\times 10^{16}cm^{-3}
1×1016cm−3和受主
3
×
1
0
19
c
m
−
3
3\times 10^{19}cm^{-3}
3×1019cm−3,且介电常数分别为12和13.求在热平衡时,各材料的静电势和耗尽区宽度。
需要用到的公式包括1.异质结的内建电势计算式
V
b
1
=
ε
2
N
2
(
V
b
i
−
V
)
ε
1
N
1
+
ε
2
N
2
V_{b1}=\frac{\varepsilon_2N_2(V_{bi}-V)}{\varepsilon_1N_1+\varepsilon_2N_2}
Vb1=ε1N1+ε2N2ε2N2(Vbi−V);
V
b
2
=
ε
1
N
1
(
V
b
i
−
V
)
ε
1
N
1
+
ε
2
N
2
V_{b2}=\frac{\varepsilon_1N_1(V_{bi}-V)}{\varepsilon_1N_1+\varepsilon_2N_2}
Vb2=ε1N1+ε2N2ε1N1(Vbi−V) 2.异质结的耗尽区宽度计算式
x
1
=
2
ε
1
q
N
1
V
b
1
x_1=\sqrt{\frac{2\varepsilon_1}{qN_1} V_{b1}}
x1=qN12ε1Vb1,
x
2
=
2
ε
2
q
N
2
V
b
2
x_2=\sqrt{\frac{2\varepsilon_2}{qN_2} V_{b2}}
x2=qN22ε2Vb2

























 5580
5580

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








