正交性,从內积开始到施密特正交化

前言

多维空间，向量和矩阵，以及正交性的概念都是欧几里得多维空间的扩展，因为人类的认知很难超越三维思考，所以我们对n维的理解往往降维到2-3维来类比，因此学习和分析这些概念和问题，三维思考是最直观的工具，在你即将迷失在矩阵空间的时候，她会像灯塔一样。。。。

內积、长度和正交性[1]

这三个概念是基础，然而并不容易搞懂。

內积

假设$u,v$是$R^n$中的向量：$$u=\left[\begin{array}{c}u1\\ u2\\ ⋮\\ u_n\end{array}\right]v=\left[\begin{array}{c}v1\\ v2\\ ⋮\\ v_n\end{array}\right]$$也可以将$u,v$视为n*1的矩阵，则这两个向量的內积（inner production）定义为$u^{T}v$，最后的结果是一个标量。另外向量的表示法为点积（dot product）$u\cdot v$，算法是一样的。$$uTv=u\cdot v=[u_1,u_2...u_n]\left[\begin{array}{c}v1\\ v2\\ ⋮\\ v_n\end{array}\right]=u_1{v}_1+u_2{v}_2+...+u_n{v}_n$$

长度和距离

因为$v^{T}v$是非负的标量，所以从二三维推广到n维，定义向量$v$的长度为內积的平方根。数学表达如下：$$||v||=\sqrt{v\cdot v}=\sqrt{v_1^2+v_2^2+v_2^2+...+v_n^2}$$进而$u和v的距离就是u-v的长度$，即$$||u-v||=\sqrt{(u-v)\cdot (u-v)}=\sqrt{(u_1-v_1{)}^2+(u_2-v_2{)}^2+...+(u_n-v_n{)}^2}$$

正交向量

这是从二维（三维）垂线的概念在欧式多维空间的推广，相对于前面的概念这部分理解起来有点烧脑了。二维空间的垂直从小学就开始学习了，通常用直角三角板来判断两条垂线是否垂直，相信讲到这里都好理解，但是向量是多维空间上的点，当然也可以理解为从原点辐射到向量坐标的一根有方向的线段。那么判断两个向量是否垂直，该怎么办呢？为了简单理解，我们从直角坐标出发：

直角坐标轴x上的所有点，都垂直于x上的所有点，对于二维向量来说，如何利用数学语言阐述这一性质呢？其实就是两个向量的內积等于零。而从几何角度来看，向量垂直（x轴上的向量（2,0）垂直于y轴上的向量（0,2）），存在这样一个性质，从x轴（2,0）到y轴上的向量（0,2）距离和y轴上的向量（-0,-2）的距离相等。

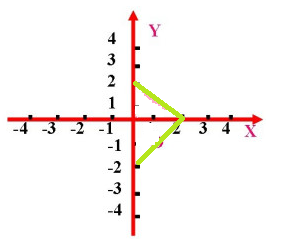
由此扩展到高维空间，从几何角度证明：$$\begin{gathered} ||u-(-v)||=||u-v|| \\ (u+v)\cdot (u+v)=(u-v)\cdot (u-v) \\ u\cdot u+u\cdot u+2u\cdot v=u\cdot u+u\cdot u-2u\cdot v \\ +2u\cdot v=-2u\cdot v \\ u\cdot v=0 \end{gathered}$$在高维空间考虑的时候，笛卡尔坐标的原点一定不能忽略，即从这个原点出发的有向线段对(向量对$u,v$)，如果满足$u\cdot v=0$，那么这两个向量被定义为正交向量（orthogonal vectors）。

非正交向量

2/3维空间两个向量不正交的情况是常见的，我们定义这两个向量夹角为$\theta$，根据余弦定理，最后可以得出內积的另外一种表达形式：$$u\cdot v=||u||||v||cos\theta$$
由此推论到高维空间向量夹角的余弦表达：$$cos\theta =\frac{u\cdot v}{||u||||v||}$$
上面这个表达被应用于机器学习里，就是余弦相似度的理论基础。

正交集，正交基和正交投影

正交集

简而言之，正交集是两两向量互相正交的一组向量集。现实中在二维空间中，直观的想象一下，不会有三个向量组成正交集，那么三维空间，最多三个向量能组成正交集，以此类推。。。在【1】中有几个定理，提到了基（basis）的概念，那么基的定义又是什么呢?

基

设V是域F上的线性空间，V中的向量集S如果满足下述两个条件：
1.向量集S是线性无关的；
2.V中每一个向量可以由向量集S中有限多个向量线性表出, 那么称S是V的一个基.【3】
打个比喻，基就像地基一样，是构建空间大厦的基础，大厦中每个横梁、竖墙都得有地基来承重。如果这组

定理1

若 S = { u 1 , . . . , u p } S=\{u_1,...,u_p\} S={u1​,...,up​}是$R^n$中非零向量构成的正交集，则$S$线性无关且是它张成的子空间的一组基。因为假设向量为正交的，所以这组基还是正交基。
上述概念最容易混淆的是线性无关和正交的概念是不是等价的？答案是否。直观的理解是线性相关可以看成平行线，线性无关是相交线，正交是垂直相交线，这样就不太容易混淆了。

正交基

$R^n$中子空间W的一组正交基是W的一组基并且本身构成正交集。【1】
这个概念有点绕，目的是为了引出下面的定理，这个定理就是正交投影的理论基础，大大简化了运算。

定理2

令 S = { u 1 , . . . , u p } S=\{u_1,...,u_p\} S={u1​,...,up​}是$R^n$中非零向量构成的正交基，对于任意$y\in W$，线性组合$y=c_1{u}_1+...+c_p{u}_p$的权重可以有下式给出：$$c_j=\frac{y\cdot u_j}{u_j\cdot u_j}(j=1,...,p)$$

正交投影

非零向量投影

给定$R^n$中一个非零向量$u$，考虑如何将$R^n$中的分量$y$分解成为两个向量的和，其中一个分量是$u$的倍数，另一个分量与$u$正交，这种表达写成：$$y=\hat{y}+z$$，其中有一个标量$\alpha$可以表达$\hat{y}=\alpha u$，$z$则是与$u$正交的向量。$$z=y-\alpha u$$根据正交概念，可以得出：$$\begin{gathered} (y-\alpha u)\cdot u=0 \\ y\cdot u-\alpha u\cdot u=0 \\ \alpha =\frac{y\cdot u}{u\cdot u} \end{gathered}$$此时，$$\hat{y}=\alpha u=\frac{y\cdot u}{u\cdot u}u$$称作向量$y$在$u$上的正交投影（orthogonal projection of y onto u)，向量$z$称作$y$中正交于$u$的分量（component of y orthogonal to u).

直线上的投影

再假设一个非零标量$c$，扩展非零向量$u$为一个线性子空间$L$有经过原点和$u$的直线，表示为$cu$，那么向量$y$在u所张成的子空间L上的投影为$$\hat{y}=pro{j}_{L}y=\frac{y\cdot cu}{cu\cdot cu}cu=\frac{y\cdot u}{u\cdot u}u$$说明向量在某个一维子空间上的投影点是唯一的，而且是L上距离y最近的一点（直角三角形在脑海里闪念一下）

空间投影

结合投影和定理2来看，一个向量$$\begin{gathered} y=c_1{u}_1+...+c_p{u}_p \\ =\sum _{j=1}^p\frac{y\cdot u_j}{u_j\cdot u_j}{u}_j \end{gathered}$$$y$则可以分解为线性空间的投影。这时要提到的如下的正交分解定理。

正交分解定理

设$W$是R^n的一个子空间。则$R^n$的每一个向量$y$都可以写成$$y=\hat{y}+z$$其中$\hat{y}\in W,z\in W^{\perp }$。若{u_1,…,u_p}是$W$的任意一组正交基，$$\begin{gathered} y=c_1{u}_1+...+c_p{u}_p \\ =\sum _{j=1}^p\frac{y\cdot u_j}{u_j\cdot u_j}{u}_j \\ z=y-\hat{y} \end{gathered}$$$\hat{y}$被称作$y$在$W$上的正交投影。

格拉姆-施密特正交化

对于$R^n$子空间$W$的一组基 { x 1 , . . . , x p } \{x_1,...,x_p\} {x1​,...,xp​},定义：$$\begin{array}{rl}{v}_1& =x_1\\ v_2& =x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}{v}_1\\ v_3& =x_3-\frac{x_3\cdot v_1}{v_1\cdot v_1}{v}_1-\frac{x_3\cdot v_2}{v_2\cdot v_2}{v}_2\\ & ⋮\\ v_p& =x_p-\frac{x_p\cdot v_1}{v_1\cdot v_1}{v}_1-\frac{x_p\cdot v_2}{v_2\cdot v_2}{v}_2-...\frac{x_p\cdot v_{p-1}}{v_{p-1}\cdot v_{p-1}}{v}_{p-1}\end{array}$$
则 { v 1 , . . . , v p } \{v_1,...,v_p\} {v1​,...,vp​}是$W$的一组正交基，两组基张成的空间是等价的： S p a n { v 1 , . . . , v k } = S p a n { x 1 , . . . , x k } ， 1 ≤ k ≤ p Span\{v_1,...,v_k\}=Span\{x_1,...,x_k\}，1\leq k \leq p Span{v1​,...,vk​}=Span{x1​,...,xk​}，1≤k≤p
首先这组基要求是线性无关，否则也不能成为“基”了。该方法提供了正交基的算法，在工程中得到广泛应用。

参考

线性代数及其应用，Lay,D,C 第三版，沈复兴等 译
麦克风阵列处理之TF-GSC 广义旁瓣相消器
线性空间的基和维数
正交与线性无关？
图解格拉姆-施密特正交化和改进的格拉姆-施密特正交化
自适应滤波：维纳滤波器——GSC算法及语音增强