# 一、Laplace变换
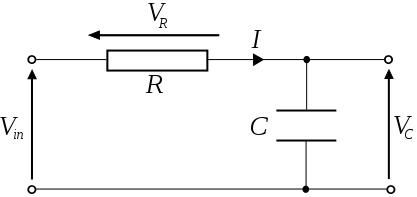
如图所示一个低通滤波器,列基尔霍夫方程,得到线性微分方程:
CdVCdt+VRR=0CdVCdt+VRR=0
正是因为电感电容的存在,使得电路方程出现微分、积分项。而Laplace变换将微分方程转化为线性代数方程,成为快速求解微分方程的有力工具。
但是列出电路的微分方程之后再进行Laplace变换,求解之后再进行反变换仍然很复杂,聪明的电子工程师们便想到直接将电路中的电阻器 (R)、 电容器 (C) 和电感元件 (L)变换到s域。
| R | L | C |
|---|---|---|
| R | sL | 1sC1sC |
于是这个电路可以看作一个分压器
VC(s)Vin(s)=1/CsR+1/Cs=11+RCsVC(s)Vin(s)=1/CsR+1/Cs=11+RCs
下面便引出系统的传输函数。
二、传递函数
对于最简单的连续时间输入信号 x(t)x(t) , 和输出信号 y(t)y(t) 来说传递函数 H(s)H(s) 所反映的就是零状态条件下输入信号的拉普拉斯变换X(s)=L{x(t)}X(s)=L{x(t)} 与输出信号的拉普拉斯变换 Y(s)=L{y(t)}Y(s)=L{y(t)} 之间的线性映射关系:
Y(s)=H(s)X(s)Y(s)=H(s)X(s)
或者
H(s)=Y(s)X(s)=L{y(t)}L{x(t)}H(s)=Y(s)X(s)=L{y(t)}L{x(t)}
而当系统为封闭回路的负反馈系统时:

由上图可得:
Y(s)=Z(s)G(s)⇒Z(s)=Y(s)G(s)Y(s)=Z(s)G(s)⇒Z(s)=Y(s)G(s)
X(s)−Y(s)H(s)=Z(s)=Y(s)G(s)⇒X(s)=Y(s)[1+G(s)H(s)]/G(s)X(s)−Y(s)H(s)=Z(s)=Y(s)G(s)⇒X(s)=Y(s)[1+G(s)H(s)]/G(s)
⇒Y(s)X(s)=G(s)1+G(s)H(s)⇒Y(s)X(s)=G(s)1+G(s)H(s)
三、零极点
传递函数可以写成如下更加普遍的形式:
X(s)=N(s)D(s)=M∏Ri=l(s−βi)∏Rj=l(s−αj)X(s)=N(s)D(s)=M∏i=lR(s−βi)∏j=lR(s−αj)
所有让分母 D(s)D(s) 为0等点 szsz 为系统的零点;
所有让分子 N(s)N(s) 为0等点 spsp 为系统的零点;
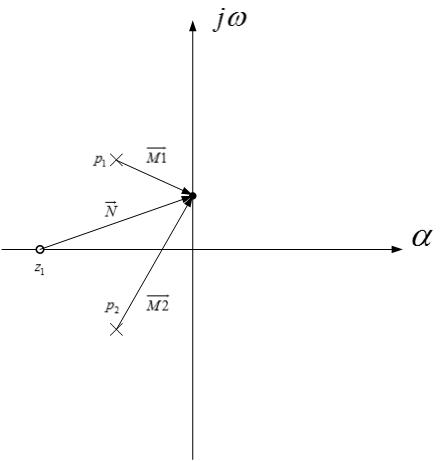
考虑一个由一个零点和两个极点组成的系统,在极坐标上表示为下图:
从上图中可以看出傅立叶变换和拉普拉斯变换的关系:
傅立叶变换为拉普拉斯变换在s平面虚轴 jωjω 上的求值。
由此,引出波特图。
四、波特图
从上图中可以看到,系统的传递函数 H(Jω)H(Jω) 其实就是将复平面中极点零点到虚轴上某一点的向量相乘除:
H(jω)=N⃗ M1→M2→=z1−jω(p1−jω)(p2−jω)H(jω)=N→M1→M2→=z1−jω(p1−jω)(p2−jω)
表示为幅度(取对数)和相位:
20log10|H(jω)|=20log10|z1−jω||p1−jω||p2−jω|20log10|H(jω)|=20log10|z1−jω||p1−jω||p2−jω|
∠H(jω)=ej(α1−α2−α3)∠H(jω)=ej(α1−α2−α3)
其中 α1,α2,α3α1,α2,α3 为图中向量的角度,由此便可以画出波特图。
下面以一个低通RC滤波器电路举例:
H(jf)=11+j2πfRCH(jf)=11+j2πfRC
ωc=1RCωc=1RC
H(jω)=11+jωωcH(jω)=11+jωωc
画出波特图如下:
下面介绍如何得到上图。
增益图
AvdB=20log|H(jω)|=20log1∣∣1+jωωc∣∣AvdB=20log|H(jω)|=20log1|1+jωωc|
=−20log∣∣∣1+jωωc∣∣∣=−10log[1+ω2ω2c]=−20log|1+jωωc|=−10log[1+ω2ωc2]
- 在角频率小于ωcωc 时,因ωωcωωc 项较小,相对 1 而言可以忽略,因此其增益值为定值1,在增益图上是一条位在 0dB 的水平线
- 在角频率大于ωcωc 时,因ωωcωωc 项较大,相对而言 1 可以忽略,因此式子简化为 −20logωωc−20logωωc , 是斜率为-20dB/十倍频的斜线
- 在角频率等于ωcωc 时,−10log[1+ω2ω2c]=−10log2=−3dB−10log[1+ω2ωc2]=−10log2=−3dB,因此该点为 -3dB 转折点
相位图
φ=−tan−1ωωcφ=−tan−1ωωc
- 其中 ωω , ωcωc 分别是输入角频率及截止角频率。 当输入角频率远小于截止角频率时,ωωcωωc比例的数值很小,因此相位角接近零度。
- 当频率增加,相位角的绝对值也随之增加。在时 ω=ωcω=ωc 时 为-45度。
- 当输入角频率远大于截止角频率时,相位角会趋近-90度。
关于波特图一点说明
注意 :通常我们说波特图中遇到一个极点幅度开始以20dB/十倍频的斜率下降,在极点处相移为-45度;零点则是幅度上升,相移45度。
有人会疑问零点、极点不应该使得传递函数为零或者无穷大吗?
其实从s平面那幅图可以看出,其实我们所谓的在波特图中遇到的零点极点,并不是s平面中由传递函数公式求解出的零点极点。只有当零点或者极点真的出现在虚轴 jωjω 上时,该频率的输入才会导致零输出或者无穷大输出。
五、稳定性
巴克豪森判据:
对于一个负反馈系统:
YX(s)=H(s)1+βH(s)YX(s)=H(s)1+βH(s)
如果 βH(s)=−1βH(s)=−1 则增益为无穷,电路产生振荡,此条件可表达为:
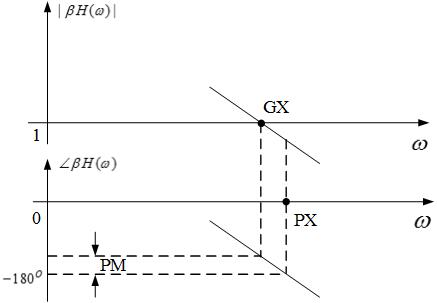
|βH(s)|≥1|βH(s)|≥1
∠βH(s)=−180o∠βH(s)=−180o
上式可以理解为,输入信号经过正向通路以及反馈回路一圈之后相移360度(环路增益的180度以及负反馈叠加点的180度),使得负反馈变成正反馈。此时如果环路增益的幅度大于1,则在输入信号上不断叠加一个放大了的信号,一个发散的数列不断叠加必然是无界的。
因此,避免振荡的放法就是在环路增益相移180度时,保证其幅度小于1。(收敛序列求和是有界的)
上图中定义了“增益交点GX“、“相位交点PX“、“相位裕度PM“等概念。(注意上图为环路增益的波特图)
奈奎斯特判据
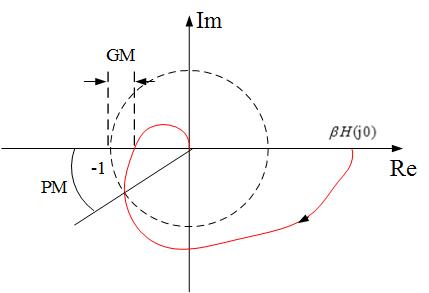
如果将波特图绘制到极坐标系中,可以得到奈奎斯特图:
图中红色的线为传递函数曲线,其与单位圆的交点为GX点,与实轴的另一交点为PX点,并且能直观地看出相位裕度,增益裕度。
另外如果-1这个点不被传递函数曲线包围,则系统是稳定的。
六、反馈、相位裕度、稳定性的关系
相位裕度
此处参照sansen书中方法
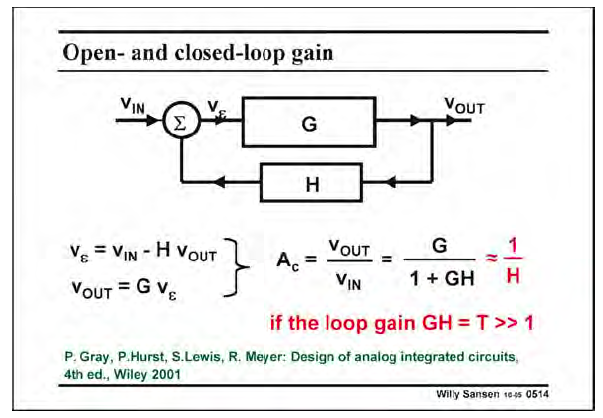
定义开环增益
AO=GAO=G
闭环增益
Ac=G1+GH≈1HAc=G1+GH≈1H
所以
dB(AOAc)=dB(AO)−dB(Ac)≈dB(GH)dB(AOAc)=dB(AO)−dB(Ac)≈dB(GH)
图中 AOAO 曲线与 AcAc 曲线差就是环路增益,因此两条曲线(实线)交点对应的频率,也即AO/Ac=1AO/Ac=1,就是环路增益降到单位增益的频率。这个点就是增益交点,可以从这个点看相位裕度。
(思考的切入点:让两条曲线相交,其实在数学上是让两个函数相等)
GBW
上图定义出增益带宽积,在闭环增益(Y/X)图中,为主极点的下降曲线与横轴的交点出的频率(单位增益)。
20logAO−10log(1+(ωωmajor)2)=020logAO−10log(1+(ωωmajor)2)=0
得出
ω≈AO×ωmajor≈Ac×ωcω≈AO×ωmajor≈Ac×ωc
注意:
- GBW点其实是约等于的结果,但在对数图中可以看作不变。
- 另外,对于多极点系统,还是看第一个主极点延长线与实轴的交点,即GBW=ω1⋅AOGBW=ω1⋅AO。
- 反馈系数改变,闭环增益相位曲线 ∠YX(jω)∠YX(jω) 是会改变的;而环路增益相位曲线 ∠βH(jω)∠βH(jω) 不变。
- sansen书中看闭环增益转折点求PM,其实它对应的是开环增益的相位图,如下图,所以不要被迷惑。之所以这样,是因为双极点系统,总相移肯定是180度。
而180度相移点是第二个极点再往右,若f2出现在GBW点右侧,则系统相对比较稳定。
相位裕度、极点位置、尖峰相互关系
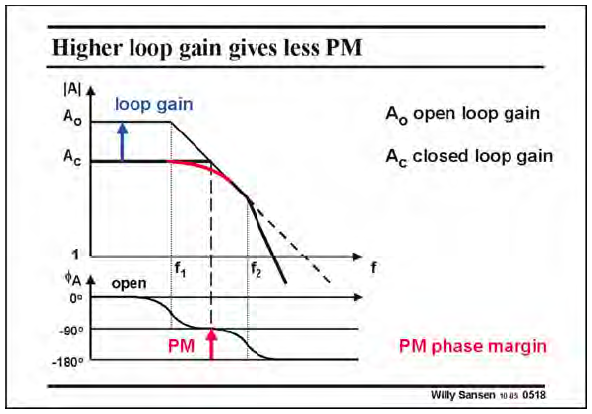
环路增益越大(图中两条曲线相差越宽),PM越小。当PM很小的时候,闭环增益曲线就会产生尖峰。

开环增益
H(jω)=AO(1+jωω1)(1+jωω2)H(jω)=AO(1+jωω1)(1+jωω2)
闭环增益
YX=H1+βH=AOβAO+jω(1ω1+1ω2)+(jω)2ω1ω2YX=H1+βH=AOβAO+jω(1ω1+1ω2)+(jω)2ω1ω2
因为 AO×ω1=GBWAO×ω1=GBW, 所以
YX≈11+jωβGBW+(jω)2βGBWf2YX≈11+jωβGBW+(jω)2βGBWf2
=11+2ζωnjω+(jω)2(ωn)2=11+2ζωnjω+(jω)2(ωn)2
其中 ζζ 为阻尼因子,ωnωn 为谐振频率。
PM的求解需要解释一下:
因为 PM=180o+∠H(GX)PM=180o+∠H(GX), 而对于双极点系统,有
∠ω=e−j(arctanωω1+arctanωω2)∠ω=e−j(arctanωω1+arctanωω2)
而对于 ω=GXω=GX 这个点,因为 GX>>ω1GX>>ω1 所以第一级已经达到90度相移。另外
GX=ω1(1+βAO)≈βω1AO=β⋅GBWGX=ω1(1+βAO)≈βω1AO=β⋅GBW
所以
PM=180o−90o−arctanGXω2=90o−arctanβ⋅GBWω2PM=180o−90o−arctanGXω2=90o−arctanβ⋅GBWω2
可得
ωn=GBW⋅ω2⋅β−−−−−−−−−−−√ωn=GBW⋅ω2⋅β
ζ=12ω2GBW⋅β−−−−−−−−√ζ=12ω2GBW⋅β
PM=90o−arctanβ⋅GBWω2PM=90o−arctanβ⋅GBWω2
结论
由信号系统知识可知:
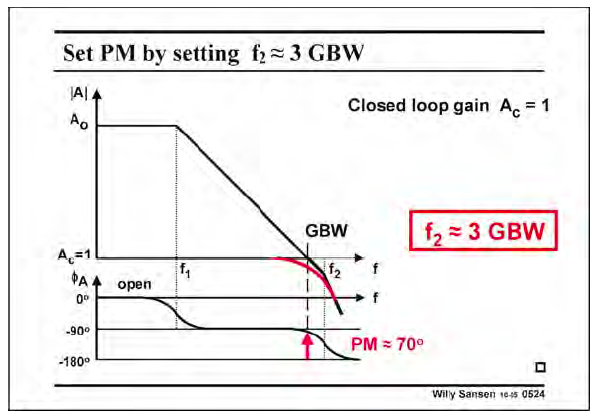
- ζ>1ζ>1, 二阶系统为两个实数极点,其实是两个一阶系统相乘;对应情况为第二个极点 ω2ω2 非常远(比如3GBW处,此时相位裕度60度~70度);
- 0<ζ<10<ζ<1, 两个共轭极点,为一个谐振系统;在闭环传输函数转折点出现尖峰。
- 第二个极点越近(ω2ω2 越小),相位裕度越小,ζζ 越小,尖峰越高,越不稳定!
有激励的输入响应

如图,输入信号为
1s−jω1s−jω
电路的传递函数为
H(s)=1sRC+1H(s)=1sRC+1
所以输出信号(s域)为
Vout(s)=1sRC+1⋅1s−jωVout(s)=1sRC+1⋅1s−jω
=As−jω+BsRC+1=As−jω+BsRC+1
其中
A=1jωRC+1↔1(ωRC)2+1−−−−−−−−−−√⋅ej(−α)A=1jωRC+1↔1(ωRC)2+1⋅ej(−α)
B=−RCjωRC+1↔RC(ωRC)2+1−−−−−−−−−−√⋅e−jαB=−RCjωRC+1↔RC(ωRC)2+1⋅e−jα
1s−jω↔ejωt1s−jω↔ejωt
1sRC+1↔e−tRC1sRC+1↔e−tRC
所以输出信号时域为
Vout(t)=1(ωRC)2+1−−−−−−−−−−√⋅ej(ωt−α)−RC(ωRC)2+1−−−−−−−−−−√⋅e−tRC⋅e−jαVout(t)=1(ωRC)2+1⋅ej(ωt−α)−RC(ωRC)2+1⋅e−tRC⋅e−jα
其中
tanα=ωRCtanα=ωRC
上式中,第一项为稳态响应,第二项是一个随时间衰减的量。这就解释了为什么我们要求系统的极点要在s平面的左半平面,这样系统才不会发散。

更新日志
2017年2月11日
来自eetop网友的两个问题补充。
问题原文:
楼主的文章仔细看过,写的很好,特来学习,有2个问题向楼主请教下:
- 其实我们所谓的在波特图中遇到的零点极点,并不是s平面中由传递函数公式求解出的零点极点,这个很难理解
- 只有当零点或者极点真的出现在虚轴 jω 上时,该频率的输入才会导致零输出或者无穷大输出。比如一对虚轴上的共轭极点,计算确实使输出无穷大,但在时域上,对应的却是一个固定幅度的正弦波,并没有振荡啊,这怎么理解呢?
问题解释:
-
问题一我觉得是因为术语的定义给人们带来了误解。
我们在信号系统还有控制理论中学过的零极点,就是系统拉普拉斯变换后传输函数的分子分母解出来的根,这个根(零点极点)可以是整个s平面上任意一个点。但是很多书中讲传输函数,波特图时候并没有把这个零点,极点的概念讲清楚。
其实我们说系统遇到一个极点,波特图开始一个20dB/10倍频的下降,很多人下意识地认为波特图横坐标对应的那个频率值就是这个极点,这是错误的,这里应该是有一个s平面到bode图的映射的。 -
问题二是正弦函数拉普拉斯变化引入的数学问题,正弦函数傅立叶变换本来就是两个冲击函数,反过来虚轴上两个共轭极点的逆变换是稳态的正弦波也就不足为奇。
这个可以参考知乎上这个解答如何理解正弦函数的傅立叶变换?
而且两个共轭极点构成一个二阶系统,二阶系统与一阶系统的分析方法有所不同。更高阶的系统最低能分解为多个一阶与二阶系统来分析。
原文链接:https://blog.csdn.net/maxwell2ic/article/details/52884914








 本文深入探讨了电路分析中的Laplace变换应用,传递函数的零极点分析,以及系统稳定性评估方法,包括巴克豪森判据和奈奎斯特判据。通过详细解析低通滤波器电路的例子,阐述了波特图的绘制方法,反馈、相位裕度与稳定性的关系,以及激励输入响应的计算。
本文深入探讨了电路分析中的Laplace变换应用,传递函数的零极点分析,以及系统稳定性评估方法,包括巴克豪森判据和奈奎斯特判据。通过详细解析低通滤波器电路的例子,阐述了波特图的绘制方法,反馈、相位裕度与稳定性的关系,以及激励输入响应的计算。















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








