如题:2019年10月

分析:没看这部分的内容。
答案:23、考切比雪夫不等式,详见问题2。指数分布数学期望是 =1/0.5=2 方差是
=1/0.5=2 方差是 =4,题目给出的是绝对值大于某个数,所以P概率要小于是D(x)/
=4,题目给出的是绝对值大于某个数,所以P概率要小于是D(x)/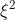 =4/16=
=4/16=
22、考的中心极限定理,详见问题4。二项分布 E(x)=np=100*0.5=50 , =
=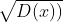 =
=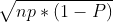 =5,没有告诉是一堆随机变量相当,只告诉n>50(也就是n很大),所以符合定理2。
=5,没有告诉是一堆随机变量相当,只告诉n>50(也就是n很大),所以符合定理2。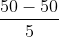 <
<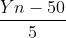 <
<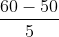

 (2)-
(2)- (0)=0.9772-0.5=0.4772.
(0)=0.9772-0.5=0.4772.  (0)=0.5??这个可以从标准正态分布的图形上来看,因为是关于x=0对称的,所以面积占了总面积的一半。
(0)=0.5??这个可以从标准正态分布的图形上来看,因为是关于x=0对称的,所以面积占了总面积的一半。
1、两大定量的意义是什么??
概率论本身是建立在大量数据观察的基础上的,抽象一下就是极限,而这两个是关于极限的定理。大数定理指随机变量的算术平均值具有稳定性,这与前面概率的本质是频率的稳定值是一个意思。而中心极限定理指随机变量极限分布符合正态分布。
2、什么是切比雪夫不等式??相比之下,里面的图更容易理解些。

有什么用呢,用来估计某个随机变量的取值是落在某个区间上的概率。也就是利用数学期望和方差来估计X概率范围,不需要知道x的分布。等价形式比较重要,因为概率极大值情形下也就是 取很大,
取很大,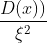 取决于方差了,当方差越小,1-
取决于方差了,当方差越小,1-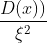 就越大,落在区间概率就越大。但肯定服从正态分布的,所以切比雪夫不等式也揭示了,概率肯定是落在某个区间内的。
就越大,落在区间概率就越大。但肯定服从正态分布的,所以切比雪夫不等式也揭示了,概率肯定是落在某个区间内的。
3、大数定理,基本不考。
4、中心极限定理??很重要。就两个内容。
- 当随机变量充大的时候,近似服从正态分布
- 一堆随机变量作和,当个数充分多时,也服从正态分布
具体的定理如下:
 一堆随机变量做和时,n足够大服从正态分布
一堆随机变量做和时,n足够大服从正态分布
 n充分大,近似看成正态分布
n充分大,近似看成正态分布








 本文深入探讨了概率论中的核心概念,包括切比雪夫不等式、大数定理及中心极限定理。详细解释了这些定理的应用场景与意义,并通过实例展示了如何运用这些原理解决实际问题。
本文深入探讨了概率论中的核心概念,包括切比雪夫不等式、大数定理及中心极限定理。详细解释了这些定理的应用场景与意义,并通过实例展示了如何运用这些原理解决实际问题。

















 573
573

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










