主成分分析（PCA）原理与实现

主成分分析（PCA）是最重要的数据降维的方法之一。针对高维数据的处理时，往往会因为数据的高维度产生大量的计算消耗，为了提高效率，一般最先想到的方法就是对数据降维。与“属性子集选择”的方法（即选择一部分有代表意义的属性直接替代原数据）不同，PCA是通过创建一个由原数据中的属性“组合”而成的，数量较小的变量集合来替代原数据。

PCA的基本思想可以这样描述：找出数据的所有属性中最主要的部分，用这个部分替代原始数据，从而达到降维的目的。显然，降维后的数据肯定会有所损失，而我们的目的，是要尽可能地保留原始数据的特征。所以，PCA的核心在于如何寻找这个“最主要部分”。

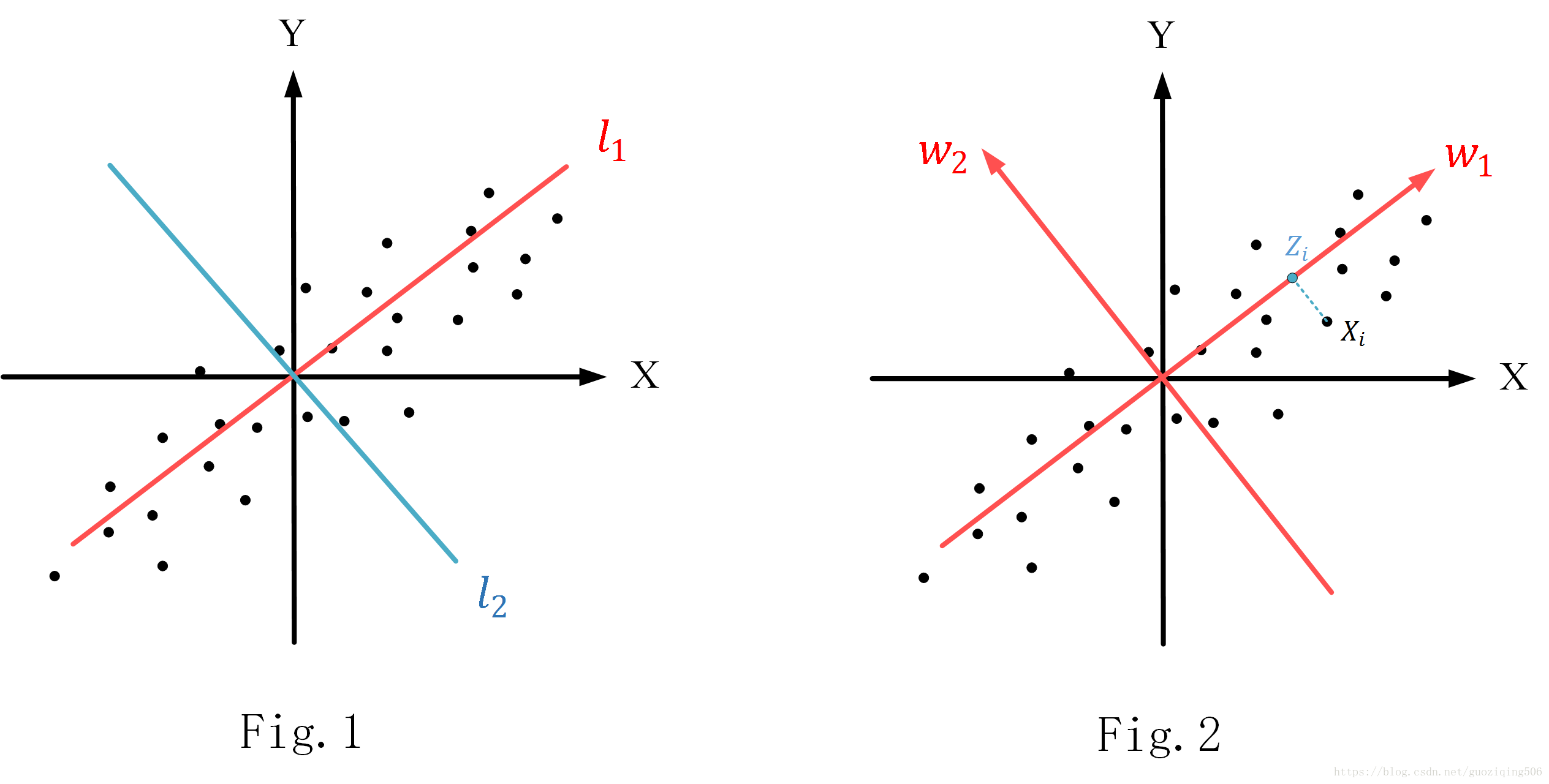
比如，现在有一组二维数据集合，如图Fig.1所示，如果要对这些二维数据降维到一维，那很容易想到在这个坐标系中找到一条直线，然后将所有的二维数据点都映射到这条直线上，我们再处理这些映射后的点，就相当于是直接对一维数据做处理了。但是找这样一条线是很讲究的，比如Fig.1中，X轴，Y轴，还有我标出的$l_1, l_2$四条线，你说映射到哪条线更好呢？显然是$l_1$，因为样本点的投影在这条直线上能够尽可能地分开，你可以理解为最大限度的保留了数据特征（反过来想，如果投影后，尽可能地分不开，那数据点不都一样了，还有啥特征、区分啊）。

PCA要解决的，就是如何找这样一条直线。当然，如果我们想要将$n$为空间的数据降到$k$维（$n > k > 0$）空间上去，那实际上找的是一个$k$维的超平面。其实，根据Fig.1我们不难发现：如果数据点集是完全无规律的随机分布，那么PCA的效果不会太好（因为不管找怎样一个超平面都会损失大量特征）；而如果数据的维度之间存在相关关系，比如某个属性与另外一个属性或者属性的组合成一定的比例关系（像Fig.1中，X与Y就基本成正比例关系），则使用PCA时非常合适的。

刚才说了，找超平面的理论依据是“在超平面上的投影点要尽可能地分开”，那换句话说，就是要找到超平面，使之具备最大的“投影方差”。下面做一个详细的推导。

PCA原理推导：基于最大投影方差

对于$m$个$n$维数据向量$\{X_1, X_2, \dots, X_m\}$，我们默认他们都已经经过了“中心化”处理，即$\sum_{i = 1}^{m}X_i = 0$，如Fig.2所示。

(1) 假设现在找到了最佳的超平面（维度是$k$），那我们旋转现有的坐标系，使其中的$k$个坐标轴组成的超平面就是我们要投影的超平面。这个过程相当于做基变换，变换过程中，我们令变换后的基是一组标准正交基，记为$W = \{w_1, w_2, \dots, w_n\}$。

WT=⎛⎝⎜⎜⎜⎜⎜w11w21⋮wn1w12w22⋮wn2……⋱…w1n