六轴姿态模块yaw角零漂去除方法_较全面的解析

在小车直线行驶时，经典也是常规的方案就是利用姿态模块、视觉模块或者红外模块等等，（还有电磁、ccd等等很多方案），但是视觉模块是很容易受到光线干扰的，很多比赛要用上opencv+树莓派才能满足要求。并且如果是要偏移一定角度，基本上也只能用姿态模块来实现。

 

本文重点在于介绍三种 六轴姿态传感器的Yaw角漂移去除 的思路，其中不乏本人自创且效果不错的程序，也是我目前在用的，以及学习了这么久，我所学到的其他两种去除思路，放在文章偏后的内容。

去除yaw角漂移，这是该模块的精髓所在，是实现小车直线、直角、偏移一定角等等操作的关键。

 

首先基础知识。

姿态模块当然常用mpu6050，或者其升级版icm20607。他们都是六轴传感器，缺少磁力计和气压计，所以z轴数据必定会出现不断增大的误差，从而造成计算出来的yaw角也会具有不断增大的误差。（明显表现为静止状态下，数值仍不断增大）

 

要使用这两个模块，首先要用通讯协议，获取这两个模块的原始数据，有很多方法，但都必须要学习I2C通讯的使用，在I2C通讯中，我们需要连续读取一片寄存器，还有使用硬件I2C，这样子才能加快我们计算的速度，减少中断时间，避免程序错误。当然硬件I2C跟软件I2C各有优缺点，有人说硬件会出错，我还没遇到过，反而软件I2C速度太慢，容易造成程序卡死，pid效率也会有影响。（具体程序具体分析）

 

原始数据来自于寄存器，并不能直接使用。所以有的人会使用别人写好的程序，或者使用dmp库。我们后面再讲dmp库是什么

 

在获取到原始数据之后，第一个必须要会的难点，就是零漂去除（注意是零漂），首先mpu6050中是要读取加速度计和陀螺仪两个部分的原始数据，对于加速度计原始数据的零漂，因为他里面含有重力加速度，这是不能去除的，所以我们要去除的是陀螺仪原始数据的零漂。

 

（静止状态下数据的一定数值，都静止了还有数值，所以他们都是硬件或者环境原因所造成的误差，就叫零漂，跟yaw角漂移区分开来）。

 

大概思路，在计算欧拉角之前，保持静止，获取一千个gx，gy，gz数据（陀螺仪三个轴的原始数据），分别算出平均值，保存为变量a，在后面正常运行获取的数据中，减去这个a，就能减去我们的零漂，从而让每次计算都能用上更精准的陀螺仪数据

 

大概代码如下：。

 

接下来，我们就要使用原始数据解算欧拉角，当然，如果使用Dmp库，甚至不用去除零漂，也不用学一堆数学知识来解算欧拉角了，但是使用了Dmp库难道就没有零漂和yaw角漂移吗？显然不会，所以dmp仍然存在更大的误差，特别是Yaw角的使用。

dmp库就是mpu6050这个模块官方推出的函数库，直接导入这个库到你的工程里面，调用他自带函数就能够直接获取mpu6050算出来的欧拉角。非常简单方便，你只需要做好通讯，什么角度都让他自己算就好了。

所以dmp虽然简单方便，难度低了，但是你的问题不会低。

 

重点！：

关于原始数据解算欧拉角，这涉及高等数学的知识，用各种公式去写出代码。网上的教程很多，但是对新手并不友好，完全不知道该做什么，也分不清什么是简单的。

（本人学浅请多指教）实际上是有多种主流方法，第一种是直接由公式计算，网上有许多推导这个公式的文章，但都是写出了矩阵公式，如何转化为代码并没有讲。这些公式涉及到矩阵计算，还有反三角函数，公式首先用加速度计数据算出欧拉角（注意无法算出yaw角），然后再用陀螺仪数据可以计算出各个角的角速度值，我们起始肯定都是0度，所以同样，陀螺仪数据也能算出欧拉角，并且yaw角也能算！

 

公式总结如下。

 

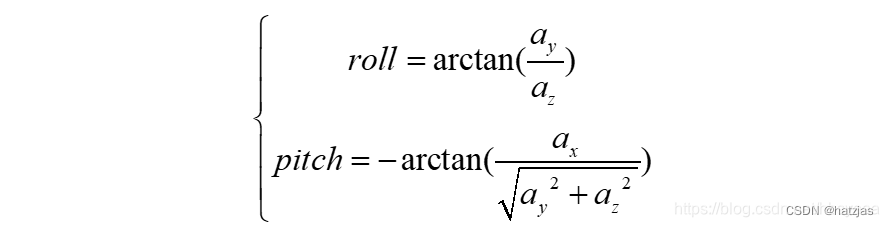
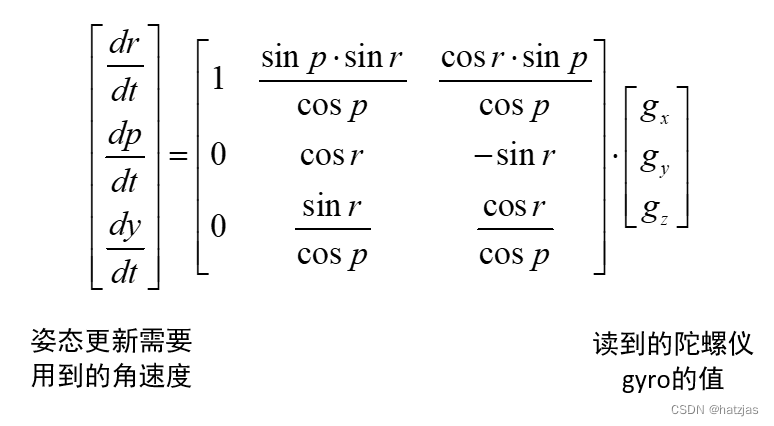
 （图片转载自他人）

这一方法一般配合一阶滤波算法，就是把加速度计算出的角度跟陀螺仪数据算出的角度进行比例融合，可以结合他们的误差特点，减少很大误差，因为加速度计只在静止状态下比较精准。

这一方法已经能得到很精准的roll跟pitch值了，但是我们的yaw角，还是因为六轴的限制，并且又不能融合（加速度计算不出yaw），种种原因导致了yaw必定存在不断变大的误差，这也是我们不能直接使用yaw的原因，必须加上其他算法，来弥补硬件不足！

 

公式转化为具体代码，网上貌似没有示例，不过也不难，学下矩阵计算就好了。加下我可以小小有偿给你发代码

 

其他方法：比如 四元数计算配合卡尔曼滤波，四元数配合二阶滤波，还有各种各样的算法，比起第一种方法，对高数要求更高了，并且不是简单看得懂的。他们都是计算方法或者滤波方法的不同，但最终都得到欧拉角，在无人机项目上，常用卡尔曼滤波算法。

 

算出角度，并且使用了滤波算法之后，即使是普通的一阶滤波，其实精度也不错了，但是你会发现，即使我们静止，即使去除了陀螺仪零漂，这个yaw角度值还是在不停地变化，这个时候，并不一定是由于算法的问题，而是你必须要知道，这是六轴姿态传感器肯定会面临的问题，就是yaw角不断变化的误差。

 

关于yaw角的作用，当然非常多，特别是无人机上，还有小车上，一般结合pid算法来使用，说白了，就是转弯角，转弯的角度，非常有用。

 

最终回到我们的重点，yaw角的漂移去除，以便我们能真正使用yaw角

 

1.第一种思路，对gz数据进行筛选，yaw角的变化是小幅度的，所以在gz上，我们可以筛选并去除那些小幅变化的数据，从而得到精准的yaw角（gz，即陀螺仪原始数据中z轴的数据，就是这个轴的数据在不断产生误差！）

 

2.第二种方法，统计误差值，进行线性回归计算。这也是很多人在用的，但是统计起来很麻烦，推荐大家可以用函数图像生成器，不用自己去做计算，不然太慢了，也不准。因为我们会发现误差是不断增加，比较符合一次函数，那我们不就能通过拟合的一次函数，计算出每个时刻的误差值吗？然后我们每次得到的yaw角，都必须减去每个时刻的误差，我们每次得到的yaw角，都存在误差

3.

！！要注意，我们只是在每次计算减去误差，实际上误差一直在yaw角中存在，我们只不过是通过计算，看见了我们想看见的yaw角

 

我在第一次用这个的时候，我在每次中断里面都减去同样的误差，因为我觉得这次减了，下次也减，那不就是一直在给yaw角做差吗？实际上是错误的，比如我们的误差是每秒增加0.08，那在第一个中断就要减去0.08，第二个中断就要减去0.16，而不是每个中断都减去0.08。因为我们并没有改变yaw实际的值，我们只是让yaw变成了我们想要看见的数值，对yaw做差，并不会让误差减小。可以具体尝试一下写出这个算法，会更理解些。

 

关于拟合曲线，就是统计误差和误差时间，比如1秒时误差5度，5秒误差25度，假设符合y=5x，那我们每次要用yaw角时，计算当时的时间，过了多久，然后乘以5，就是误差大小，再用yaw值减去误差就好了

 

这个思路已经能得到比较精准的yaw角的，除非你的程序要运行几十分钟甚至几个小时，这样误差会更加不可控，不好拟合。

 

并且这个算法的问题在于，我们不可能在每个时刻都得到很精准的值，算出来的值可能偏大也可能偏小，因为他实际上误差并不是线性的，只不过类似于线性。

 

第二个问题在于，，每个模块的误差变化都不一样，甚至你启动电压不一样，也会造成误差变化的不一样，这是经常遇到并且很难解决的问题！

总不可能每种情况，每个单片机，都做线性回归，这样工作量太大了，也没必要。我们只能做最贴切使用情况的线性拟合，并且单片机还不能换，芯片烧坏了又得重新拟合，所以这个方法在小项目精度还行，但是我觉得并不好用。

 

第三种，也是我自己想到的，目前在用的。所以网上肯定没人讲到这个东西。他也不难，但是你又可能想不到、并且学不到这个思路。虽然他才短短几行，但是他也比较宝贵，希望大家都对mpu6050能更加熟悉，理解跟用好

 

大概：

if（error＜0.008）erro_sumr+=error

error=yaw-yaw_last

yaw-=error

 

实际上就是，如果yaw值变化小，我们就认为他没有变化，是误差所产生的变化。所以我们要忽略掉这些变化。经过实践，！我们只要筛选掉 每5ms内，yaw角变化在正负0.008°内 的yaw值，我们就已经能基本上无视yaw的误差了！，对于自增或者自减，对于不同环境下的姿态模块，全都适用且简单！

我们会发现他是去掉小角度变化，如果我们走直线时角度变化本来就比较小呢？会不会影响到正常数据？会不会影响到精度。

其实，完全不会影响走直线的问题，因为5ms变化正负0.008，是非常小的值。但是对正常数据的影响，肯定是有的，只要你对六轴姿态模块学的好，其实你就要知道，这个误差是不可能完全消除的，软件上，程序上，永远只是减小误差。

 

这个方法非常简单好用，完全足够mpu6050进行直线，直角弯，转指定角度等任务，并且不用做线性回归等复杂操作。但是有缺点，就是会对正常的角度变化数据产生影响，，但是这个影响基本可以忽略。同样的要注意，我们要在每个中断中累加我们记下来的需要忽略的角度值，然后减去这个累加的值，每次都需要累加。因为还是那句话，我们并没有让误差消失，我们只是让他不再显示，误差在每次计算得到的yaw值中仍然在不断累加。

 

如果你静止不动，这个算法甚至可以让yaw也完全没有变化，第一次实现的时候，还是很让人震惊的，如果你被这个误差一直困扰的话。

 

再回到第一种方法，其实他跟第三种有点像，但是第三种的好处在于，dmp库同样能用，因为dmp库完全接触不到gz这种原始数据！

 

这个算法具体的代码，或者其他各种模块的代码，如编码器测速，超声波，串口通讯等等，有需要的可以联系我，小小有偿获取。也可以联系我，相互指导学习。