目标跟踪（最全最详细的卡尔曼滤波法：原理+代码）【西电电子信息综合实验四】

目标跟踪（最全最详细的卡尔曼滤波法：原理+代码）【西电电子信息综合实验四】

这里只讨论线性滤波方法，非线性滤波在这里不讨论

一.状态方程描述

若讨论二维匀速模型，可以非常容易的得出位置状态转移的方程

​

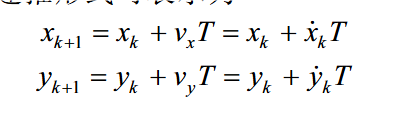
也可以非常容易的得到速度状态转移的方程

​

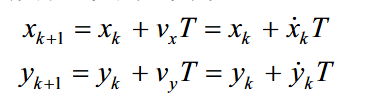
如果讨论过程噪声：就是目标不可能做绝对匀速运动，其速度必然有一些小的随机波动，例如目标在匀速运动过程中，
驾驶员或环境扰动等都可造成速度出现不可预测的变化，像飞机飞行过程中云层和阵风
对飞机飞行速度的影响等，而这些速度的小的变化可看作过程噪声来建模

那么加上过程噪声之后的位置状态转移方程为，

​

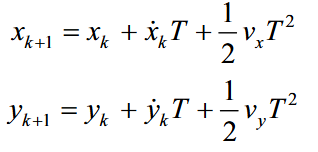
加上过程噪声之后的速度状态转移方程为

​

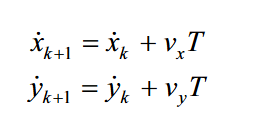
用矩阵的形式表达为：

​

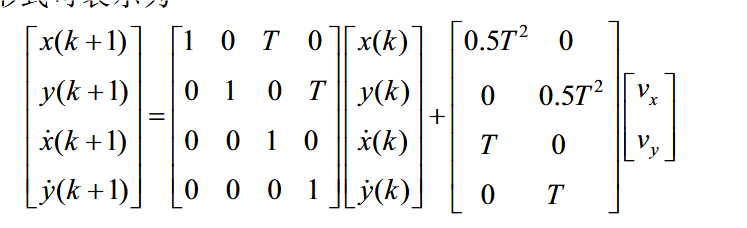
有状态转移方程

​

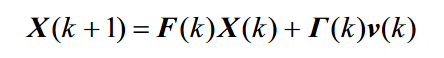
可以得到状态转移矩阵 :F(K)

​

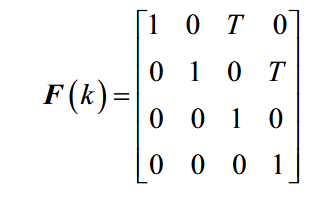
按照教案，只考虑零均值的高斯白噪声模型为

=​

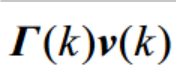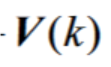
那么有状态转移方程

​​

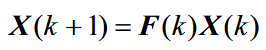
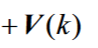
二.量测方程：是雷达测量过程的假设，对于线性系统而言量测方程可表示为

​

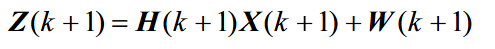
符号解释：Z（k+1）为量测向量；H（k+1）为量测矩阵；W（k+1）为具有协方差 R（k+1）
的零均值、白色高斯量测噪声序列

又因为状态向量为：

​

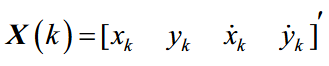
量测向量为：

​

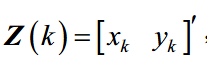
因此为了满足量测方程，有量测矩阵H(X):

​

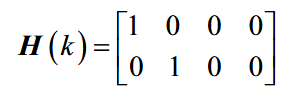
三.卡尔曼滤波方法

根据最小均方误差推导得出

​

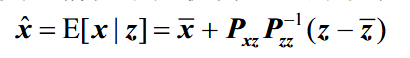
通过卡尔曼算法，通过新息与卡尔曼增益的乘积加上状态的第一步预测，得到状态的最终预测值

​

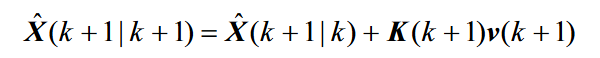
这里的新息是量测的估计值和量测的预测值的差值

卡尔曼增益由状态向量和量测向量的协方差矩阵构成

这一段内容很难看懂，不过，本质上，就是通过量测和状态，预测出下一个点的状态向量，接下来会详细解释其过程

具体步骤如下：

1.状态的第一步预测：

​

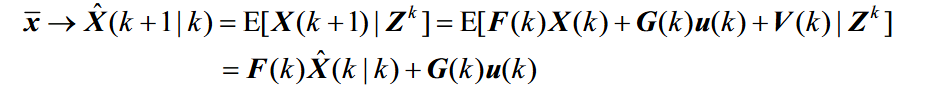
上面的G(K)*U(K)是控制量这里不予讨论，忽略得到状态第一步预测的简化方程

​​​

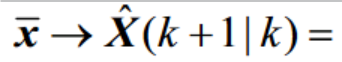
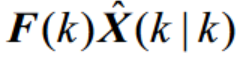
2.量测的预测值

​

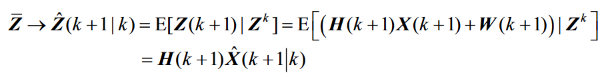
3.状态值误差

由状态值的估计值减去状态预测值的第一步预测值得到

​

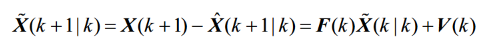
4.衡量预测协方差矩阵

​
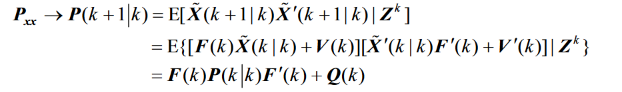
这里的 Q矩阵是合成噪声矩阵，我们假设各噪声相互独立，且都是零均值的高斯白噪声，那么该矩阵为单位矩阵，所以后面的噪声合成矩阵我们都假定为单位矩阵。
这里用估计值减去预测值，再衡量协方差，其意义是通过协方差矩阵衡量预测的不确定性

协方差越小，预测准确性越大，不确定性越小。

5.量测值误差（新息）

由量测值的估计值减去量测预测值的第一步预测值得到

​

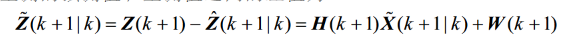
也可以用v（k+1）表示新息

​

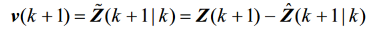
6.衡量量测协方差矩阵（新息协方差矩阵）

同理可得

​

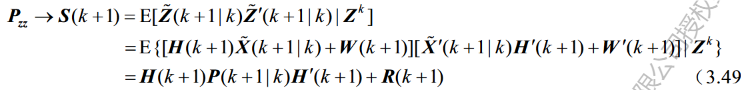
同理，其也能衡量新息的不确定性，协方差越小，预测准确性越大，不确定性越小

7.状态与量测之间的协方差矩阵

​

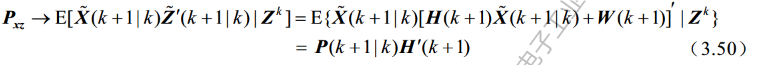
8.衡量最小均方误差所得到的预测值

由​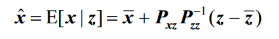

有​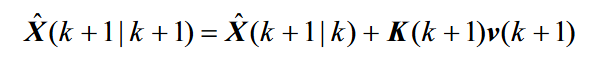

由上下恒等式可以推出卡尔曼增益：

​

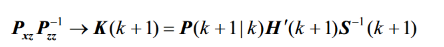
这样就能计算出卡尔曼增益，也就能通过量测和状态量预测出下一个状态量了！

9.协方差更新方程为

​

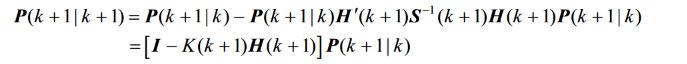
这里相减的理解是融合克尔曼增量到新的协方差中，这里的推导可以理解为在更新状态后，如何将新观测的不确定性融入到状态协方差中。通过 $K_k$ 的引入，我们能够调整协方差，使其反映观测对状态估计的不确定性影响。（说实话这一步不是很懂，能用就行）

整理，简化之后，可以得到以下算法流程

四.算法流程

1. 初始设定

在卡尔曼滤波中，状态模型可以表示为：
$x_k=F{x}_{k-1}+w_k$

其中：

(x_k) 是时刻 (k) 的状态向量。

(F) 是状态转移矩阵。

(w_k) 是过程噪声，通常假设为均值为零的高斯噪声，协方差为 (Q)。

观测模型为：
$z_k=H{x}_k+v_{}$