一篇图文详解PID调参细节，实现PID入门到精通

古-月

于 2025-05-15 10:00:00 发布

阅读量961

点赞数 28

文章标签： ROS应用

本文链接：https://blog.csdn.net/hcx25909/article/details/147892438

版权

读完本篇文章你的收获：

PID三个参数基本概念
了解如何调节PID
认识一个钻研技术的博主

先上效果图：

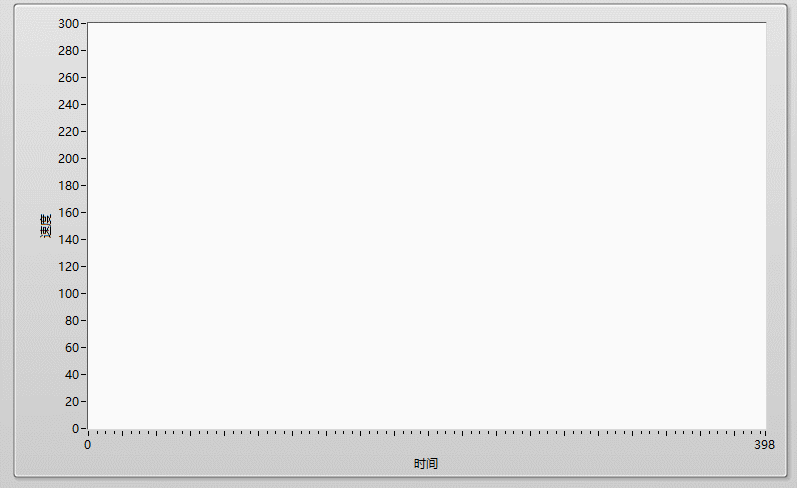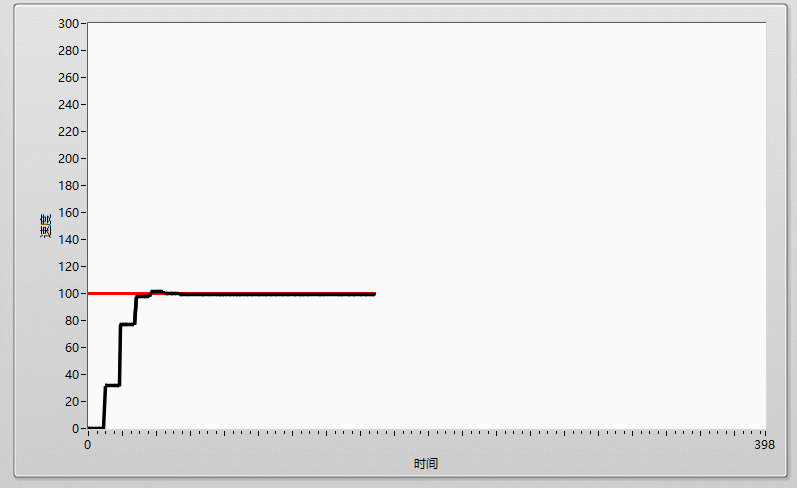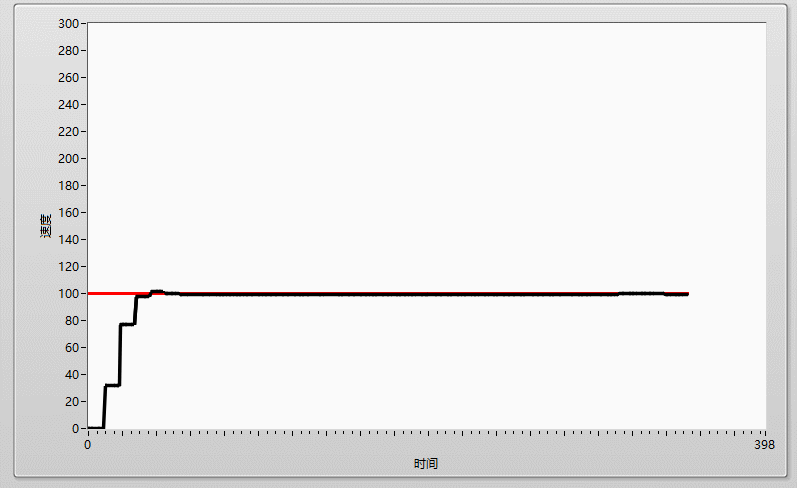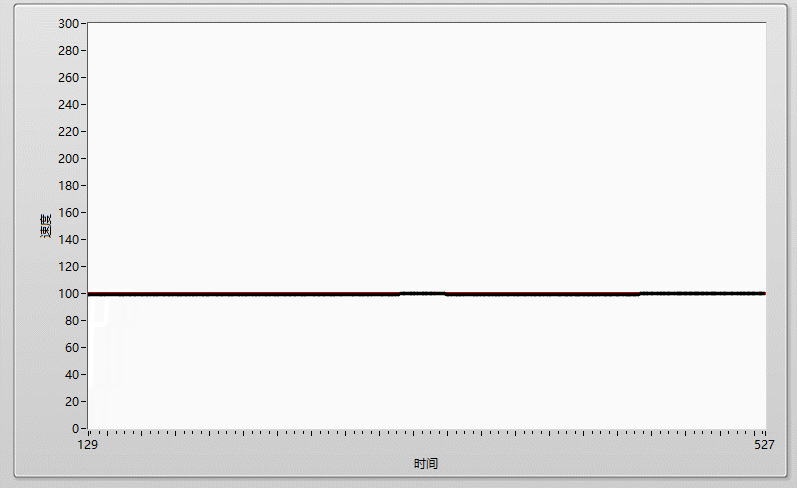
一、什么是PID

在工程中，如果我们要用单片机做一个温控系统，其系统组成一般如下：一个采集温度的ADC，一个输出温度的加热头以及一个用于运行控制算法的单片机，如果我们要维持温度为100度，在不加任何控制算法的情况下，我们可以通过简单的阈值判断法来控制温度，一个if判断语句，当采集到的温度大于100时，单片机控制加热头关闭，当采集的温度小于100度时，单片机则控制加热头开启，简单粗暴，但这样的控制方法，最终所展示出来的温度曲线是极其不稳定的，他会由于控制器件的灵敏程度、加热头的性能等等原因，导致最终的温度曲线会在目标周围震荡，达不到理想的控制效果，就像下图：实际曲线（黑线）在目标曲线（红线）周围抖动

那如何才能维持实际曲线与目标曲线贴合，达到一个稳定的控制效果呢？

这里就引入了PID控制算法的概念，PID是 Proportion Integration Differentiation 的缩写，实际上他就是一个公式，由比例项（Proportion ），积分项（Integration ），微分项（Differentiation） 三个部分组成，具体形式就是下面的公式：

其中err(t)就是当前值和目标值的误差，PID的公式就是对这个误差分别进行比例、积分、微分处理后叠加输出，因为比例计算、积分计算、微分计算在数学公式上的计算定义不同，所以对应的项的输出特性和输入特性也有着不同，具体解释如下：

1. 比例系数

比例控制系数，实际上就是先简单的定义输入与输出的线性关系，假如我们输出控制量的值得范围在 100-1000，输入的err误差范围却在0.001-0.1；当误差为0.1的时候输出量需要到达到1000，这时我们就需要通过比例系数来构建输入与输出的线性关系

2. 积分系数

上一点我们分析了比例系数的含义，有小伙伴可能会好奇，比例系数加上后的效果其实和阈值判断原理没什么区别，确实是这样，只用上比例系数的效果和阈值判断没什么区别，但别忘了，PID后面还有I和D两项，其中I项的理解我们可以从积分的含义来理解，积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲形的面积值，这个曲线就是err(t)的函数，这个积分面积值就是代表过去一段时间的误差累计值，我们把这个累计值乘以系数进行变换后，叠加到输出上，就可以一定程度上消除历史误差对当前实际曲线的影响，提高系统的稳定性

3. 微分系数

微分的数学理解可以理解为当前误差曲线的斜率，他可以用来预测当前曲线的未来走势，对微分项的值进行处理后叠加，就可以预测当前值的未来趋势，提高系统对未来变化反应能力

二、PID调节方式

通过上一小节的分析，我们对PID的三个项有了一个简单的理解，但文字上的描述还是太抽象了，我以一个小车调速系统来做进一步讲解，结合实际现象来分析PID三个参数的实际作用，以及如何调这三个参数，用到的实验平台如下

平衡小车之家的主控板及电机
自己编写的调试上位机

控制系统图片：

上位机界面：

我们在使用PID的时候，单独只使用一个参数是没有意义的至少使用两个参数，并且P（比例项）是必须要有的，虽然PID有三个参数，但大多数情况下PID三个参数并不是都使用上的，一般会其中两个来组合使用，比如PI组合用于追求稳定的系统，PD组合用于追求快速响应的系统，当然PID用于即追求稳定又追求快速响应的系统，但是实际上PID参数越多越难调，而且许多情况下两个参数的效果已经足够了，所以我一般根据情况使用前两个，下面对这几个系统都做一个分析