通用二维复合变换和计算效率
表示平移、旋转和缩放组合的通用二维变换可以表示为矩阵等式1:
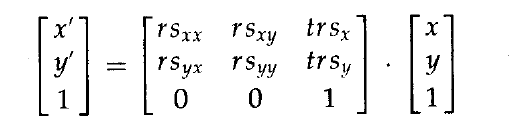 4个元素rsjk是变换中(仅包含旋转角和缩放系数)的多重旋转-缩放项。元素trsx和trsy ,是包含平移距离、基准点和固定点坐标以及旋转角和缩放参数组合的平移项。例如,如果一个对象要对于其中心坐标(xc,yc)进行缩放、旋转和平移,那么复合变换矩阵的元素值为:
4个元素rsjk是变换中(仅包含旋转角和缩放系数)的多重旋转-缩放项。元素trsx和trsy ,是包含平移距离、基准点和固定点坐标以及旋转角和缩放参数组合的平移项。例如,如果一个对象要对于其中心坐标(xc,yc)进行缩放、旋转和平移,那么复合变换矩阵的元素值为:
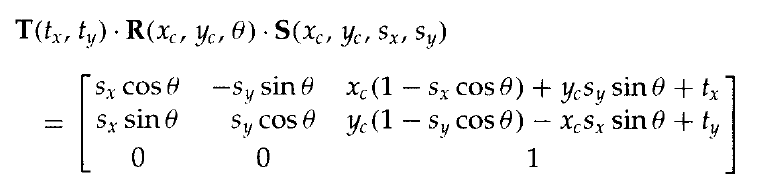 尽管矩阵等式1需要9次乘法和6次加法,但变换后的坐标的显示计算为等式2:
尽管矩阵等式1需要9次乘法和6次加法,但变换后的坐标的显示计算为等式2:
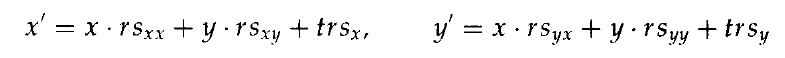 因此,实际上变换坐标位置仅需完成4次乘法和4次加法。一旦把单个矩阵连接起来计算出复合矩阵的元素值,这就是任何变换序列所需计算的最大数目。假如没有合并,那么每次都要使用一个单独的变换,则计算的数目将大大增加。因此,变换操作的有效实现是先形成变换矩阵,合并所有变换序列,然后用等式2计算变换的坐标。在并行系统上,使用等式1的复合变换矩阵而直接进行矩阵相乘也可以有相同的效果。
因此,实际上变换坐标位置仅需完成4次乘法和4次加法。一旦把单个矩阵连接起来计算出复合矩阵的元素值,这就是任何变换序列所需计算的最大数目。假如没有合并,那么每次都要使用一个单独的变换,则计算的数目将大大增加。因此,变换操作的有效实现是先形成变换矩阵,合并所有变换序列,然后用等式2计算变换的坐标。在并行系统上,使用等式1的复合变换矩阵而直接进行矩阵相乘也可以有相同的效果。
由于旋转计算需要对每个变换点进行三角求值和多次乘法,因而在旋转变换中的计算效率就成为十分重要问题。在动画及其他包含许多重复变换和小旋转角的应用中,我们可用近似和循环计算来减少复合变换方程中的计算量。当旋转角较小时,三角函数可用其幂级数展开式的前几项的近似值来代替,对于足够小的角度(小于10° ), cosθ近似为1,而sinθ的值非常接近于θ的弧度值。例如,假如以小角度步长绕原点旋转,那么可以将 cosθ设置为1.0,并在每一步中将变换计算减少为两次乘法和两次加法:
其中,只要旋转角不变化,sinθ对所有的步长只需求值一次。在每一步中,由这种近似所引起的误差随旋转角的减少而减少。但即使是使用较小的旋转角,很多步之后的积累误差也会变得很大。如果要通过消除每一步中x′和y′的误差来控制积累误差,则必须在误差积累变得太大时重新设置对象位置。有些动画应用自动地在固定间隔处重设对象位置,如每360°或180°。
复合变换经常包括逆矩阵计算。例如,对于通用缩放方向及对于反射和错切的变换顺序,可以使用逆旋转分量进行描述。我们已经注意到,基本几何变换的逆矩阵表示可以使用简单程序生成,逆平移矩阵可以通过改变平移距离的符号而得到,逆旋转矩阵通过完成矩阵转置(或改变sin项的符号)而得到,这些操作比直接逆矩阵计算要简单得多。
表示平移、旋转和缩放组合的通用二维变换可以表示为矩阵等式1:
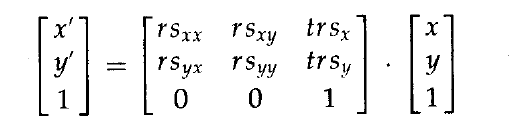
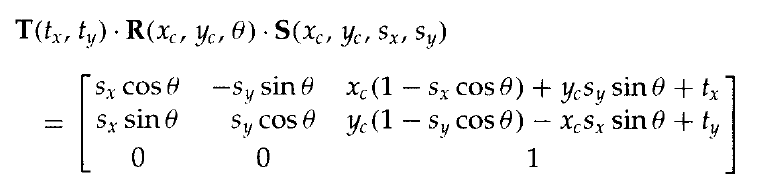
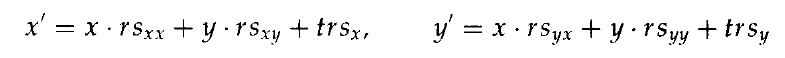
由于旋转计算需要对每个变换点进行三角求值和多次乘法,因而在旋转变换中的计算效率就成为十分重要问题。在动画及其他包含许多重复变换和小旋转角的应用中,我们可用近似和循环计算来减少复合变换方程中的计算量。当旋转角较小时,三角函数可用其幂级数展开式的前几项的近似值来代替,对于足够小的角度(小于10° ), cosθ近似为1,而sinθ的值非常接近于θ的弧度值。例如,假如以小角度步长绕原点旋转,那么可以将 cosθ设置为1.0,并在每一步中将变换计算减少为两次乘法和两次加法:
其中,只要旋转角不变化,sinθ对所有的步长只需求值一次。在每一步中,由这种近似所引起的误差随旋转角的减少而减少。但即使是使用较小的旋转角,很多步之后的积累误差也会变得很大。如果要通过消除每一步中x′和y′的误差来控制积累误差,则必须在误差积累变得太大时重新设置对象位置。有些动画应用自动地在固定间隔处重设对象位置,如每360°或180°。
复合变换经常包括逆矩阵计算。例如,对于通用缩放方向及对于反射和错切的变换顺序,可以使用逆旋转分量进行描述。我们已经注意到,基本几何变换的逆矩阵表示可以使用简单程序生成,逆平移矩阵可以通过改变平移距离的符号而得到,逆旋转矩阵通过完成矩阵转置(或改变sin项的符号)而得到,这些操作比直接逆矩阵计算要简单得多。

























 7751
7751











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








