第十章 无穷级数

常数项级数

什么是常数项级数

就是每一项都是常数的无穷项累加

主要考点在敛散判断，
发散通常就是S = 无穷

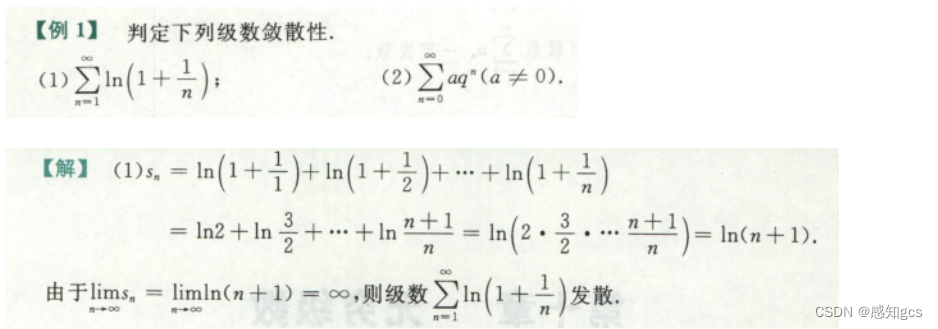
直接展开计算

等比数列求和，有公式

性质

级数S收敛，kS也收敛
级数u和级数v收敛，u+v也收敛
不存在 + 存在 = 不存在
不存在+ 不存在 = 不确定

注意

1. 级数的敛散性只与后无穷项有关
2. 收敛级数加括号收敛且和不变
1. 级数加括号收敛，原级数不一定收敛，如 1-1+1-1…
2. 级数加括号后发散，原级数一定发散，部分发散，整体一定发散

级数收敛的必要条件

对1举个反例，如1/n的级数发散，但是极限lim un = 0

常数项级数审敛准则

3类审敛法

这部分考题的重点，分成3个部分，

1）是正项级数，就是每一项都大于0，
有4个办法，先用34，比值法和根值法，再用12比较判别法和比较法的极限形式（需要缩放，不好做）

34方法的思想是等比数列的类比

12方法，大收小也收，小散大就散，2和1差不多意思，（2)的①同敛散转换用的挺多

常用的缩放结论：

p级数
1/n发散很经典

等比求和

2）交错级数，就是一个正数，一个负数，交错的级数，
用莱布尼茨准则，数列单调 且 lim un=0，则交错级数收敛

注意反之不成立

3）任意项级数

用加绝对值的方法，转换成正项级数，若绝对值|S|收敛，则S必收敛，因为大收敛小必收敛

或者利用条件收敛，条件收敛的正/负项构成的级数一定发散，
这是因为S收敛了，而|S|发散，一种特殊情况是S是一正一负抵消了，单独把正项和负项提出来则必发散

推导：un±|un| => 收敛±发散 = 发散

例题

A） an=bn是一个交错级数 -1n/√n， anbn = 1/n发散

B） an=bn=1/n， anbn = 1/n2 收敛

C）正确

∑|bn|收敛，lim an=0，an有界，|an| <= M,
|anbn| <= M|bn|, M|bn|收敛，则|anbn|收敛

∑|an|收敛，正项级数收敛，则lim |an| -> 0（0 <=lim |an|< 1），
an2 <= |an|，则∑an2收敛

有两个结论，

∑|bn|收敛，lim an ->0，则∑|anbn|收敛
∑|an|收敛，则 ∑an2收敛

D）an=bn=1/n，an2bn2收敛

A 正确定理，级数收敛，级数加括号也收敛，反之不成立，BD错误
C，un若为交错级数前项加后项抵消，改成减必发散

幂级数

定义

什么是幂级数？

类比一下泰勒展开，泰勒展开最后高阶无穷小代替，而幂级数是n->无穷的累加和

幂级数定理

1） 阿贝尔定理

幂级数S(x)的收敛半径和收敛域的由来

2）幂级数收敛性质只有下面三种可

收敛半径、收敛区间和收敛域

注意：

条件收敛则一定是收敛区间的一个端点，刚好是一个临界状态，∑anxn收敛，∑|anxn|发

求收敛半径的两个方法，比值法和根值法，这和？什么很像

幂级数性质

1）有理运算性质：加减乘除

R是R1R2中小的那个

anxn·bnxn的系数是有规律的，注意xn的系数：a的i从0到n，b的j从n到0，aibj累加

分析性质，

连续性：收敛区间内连续
可导性和可积性：级数项乘一个或者除一个数不影响收敛区间

例题

求收敛半径就两个求法，比值和根值，注意使用系数算

要求收敛区间，先求收敛半径，收敛区间=（x0-R，x0+R）

难点：判断端点处，x=常数R，变成常数项级数，判断的收敛性，用3类审敛法（正项，交错，任意）

系数一样中心不一样 => 收敛半径一样，收敛域平移

这题考的是阿贝尔定理和收敛域平移

破题关键在于：幂级数定理（条件收敛的临界状态），还有一个思想要掌握是幂级数在x=x0处是常数项级数

级数an在x=1时条件收敛，则an(x-1)在x=2的时候条件收敛，则2是一个端点，x=1又是中心，可以求出收敛区间(0,2)

函数的幂级数展开

定义

函数表示成幂级数形式，一种趋近的思想，化曲为直

展开幂级数的两种方法：

直接法，用下面的定义
间接法，用7个常用公式去凑

幂级数展开的必要条件是fx任意阶可导，

展开中心x0的改变会改变收敛区间，展开中心与收敛半径的关系为（x0-R，x0+R）

定理

展开式唯一

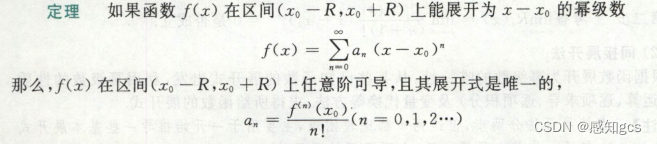
泰勒级数

这个其实就是泰勒公式，很熟悉的形式

fx任意阶可导 => 泰勒级数在收敛区间内收敛与fx 【充要条件】是 lim Rn = 0

常用展开式（背

例题（幂级数展开

分母因式分解，1/2-x的处理是提一个1/2 分母化成1-x的形式

老样子，分母因式分解拆项，分母提项化成 1/1±x的形式

求导数的级数展开，在积分

例题（级数求和

求收敛域，先求半径，判断端点
已有公式1/1-x转换=∑xn，原式 = x∑nxn-1，x∑(xn)’

已有公式 1/1+x = (-1)n-1 xn

分母拆项，

常用结论： ∑xn/n = - ln(1-x)

提一个x出去，累加项的导数S’x变成某个函数的级数，两边求积分，注意不是不定积分，
S‘x求积分Sx是变上限积分∫x->0 S’t dt

傅里叶级数

傅里叶级数主要研究周期函数，fx用级数来表示

主要记住an bn和傅里叶级数的写法

an和bn就只差了cos和sin，a是cos，b是sin

狄利克雷收敛定理

fx在[-pai,pai]连续且只有有限个第一类间断点，且最多只有有限个极值点，则fx在区间里处处收敛。且有3个收敛公式：连续点，间断点，端点

函数展开公式

周期2Π省略，l改成Π即可

用到了积分性质的奇偶性

奇延拓和偶延拓

例题（狄利克雷收敛定理

狄利克雷收敛定理，1是端点，S(1)收敛于f(-1+)+f(1-)/2

函数展开只有bn，an = ∫ fxcosnx = 0，说明fx是奇函数，Sx从题也可以看出是奇函数，S(-1/2) = -S(1/2)，用狄利克雷收敛定理Sx=fx

例题（函数展开傅里叶级数

周期为2，2l=2，l=1，
函数在区间上连续，且为偶函数，
求an、a0即可，bn=0，根据定义写出傅里叶级数
fx写成傅里叶级数，当x=x0时化成某些特殊的常数项级数

展开3部分走，

定周期T=2l，确定l，
求an、a0、bn
写级数展开
这里还考了奇偶延拓，展开成余弦，说明fx是偶函数，偶延拓