原帖:http://zh.wikipedia.org/wiki/%E7%90%83%E5%9D%90%E6%A0%87%E7%B3%BB
球坐标系[编辑]
在数学里,球坐标系(英语:Spherical coordinate system)是一种利用球坐标 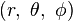 表示一个点 p 在三维空间的位置的三维正交坐标系。
表示一个点 p 在三维空间的位置的三维正交坐标系。
右图显示了球坐标的几何意义:原点与点 P 之间的径向距离  ,原点到点 P 的连线与正 z-轴之间的天顶角
,原点到点 P 的连线与正 z-轴之间的天顶角  ,以及原点到点 P 的连线,在 xy-平面的投影线,与正 x-轴之间的方位角
,以及原点到点 P 的连线,在 xy-平面的投影线,与正 x-轴之间的方位角  。
。
标记[编辑]
在学术界内,关于球坐标系的标记有好几个不同的约定。按照国际标准化组织建立的约定 (ISO 31-11) ,径向距离、天顶角、方位角,分别标记为 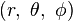 。这种标记在世界各地有许多使用者。通常,物理界的学者也采用这种标记。而在数学界,天顶角与方位角的标记正好相反:
。这种标记在世界各地有许多使用者。通常,物理界的学者也采用这种标记。而在数学界,天顶角与方位角的标记正好相反: 被用来代表天顶角,
被用来代表天顶角, 被用来代表方位角。数学界的球坐标标记是
被用来代表方位角。数学界的球坐标标记是  。这种标记的优点是较广的相容性;在二维极坐标系与三维圆柱坐标系里,
。这种标记的优点是较广的相容性;在二维极坐标系与三维圆柱坐标系里, 都同样地代表径向距离,
都同样地代表径向距离, 也都同样地代表方位角。本条目采用的是物理标记约定。
也都同样地代表方位角。本条目采用的是物理标记约定。
定义[编辑]
假设 P 点在三维空间的位置的三个坐标是 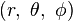 。那么, 0 ≤ r 是从原点到 P 点的距离, 0 ≤ θ ≤ π 是从原点到 P 点的连线与正 z-轴的夹角, 0 ≤ φ < 2π 是从原点到 P 点的连线在 xy-平面的投影线,与正 x-轴的夹角。
。那么, 0 ≤ r 是从原点到 P 点的距离, 0 ≤ θ ≤ π 是从原点到 P 点的连线与正 z-轴的夹角, 0 ≤ φ < 2π 是从原点到 P 点的连线在 xy-平面的投影线,与正 x-轴的夹角。
这里, 代表天顶角,
代表天顶角, 代表方位角。 当
代表方位角。 当 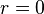 时,
时, 与
与  都一起失去意义。当
都一起失去意义。当  或
或  时,
时, 失去意义。
失去意义。
如想要用球坐标,找出点 P 在空间的地点,可按照以下步骤:
- 从原点往正 z-轴移动
 单位,
单位, - 用右手定则,大拇指往 y-轴指,x-轴与 z-轴朝其他手指的指向旋转
 角值,
角值, - 用右手定则,大拇指往 z-轴指,x-轴与 y-轴朝其他手指的指向旋转
 角值。
角值。
坐标系变换[编辑]
三维空间里,有各种各样的坐标系。球坐标系只是其中一种。球坐标系与其他坐标系的变换需要用到特别的方程式。
直角坐标系[编辑]
使用以下方程式,可以从球坐标变换为直角坐标:
-
 、
、
-
 、
、
-
 。
。
特别注意,必须依照  所处的象限来计算正确的反正切值。 也可以使用arccos来计算方位角phi的值,这样在x为0的情况下比较方便,x为0时arctan(y/x)无效.
所处的象限来计算正确的反正切值。 也可以使用arccos来计算方位角phi的值,这样在x为0的情况下比较方便,x为0时arctan(y/x)无效.
反过来,可以从直角坐标变换为球坐标:
-
 、
、
-
 、
、
-
 。
。
地理坐标系[编辑]
地理坐标系是球坐标系的第二个版本。它主要是用在地理学。通常在地理学里, 会被用来表示高度,或者完全不被使用。
会被用来表示高度,或者完全不被使用。
纬度的定义域是 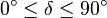 ,南纬或北纬。使用以下方程式,可从纬度
,南纬或北纬。使用以下方程式,可从纬度  变换为天顶角:
变换为天顶角:
 :北纬,
:北纬, ,
,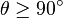 :南纬,
:南纬,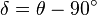 。
。
经度  的定义域是
的定义域是  。设定经过伦敦格林维治天文台的子午线为经度
。设定经过伦敦格林维治天文台的子午线为经度 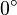 ,往东或往西
,往东或往西  度。使用以下方程式,可从经度变换为方位角
度。使用以下方程式,可从经度变换为方位角
 :往东,
:往东,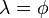 ,
,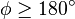 :往西,
:往西, 。
。
圆柱坐标系[编辑]
圆柱坐标系是极坐标系在三维空间往 z-轴的延伸。  坐标用来表示高度。使用以下方程式,可以从球坐标变换为圆柱坐标
坐标用来表示高度。使用以下方程式,可以从球坐标变换为圆柱坐标  :
:
-
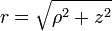 、
、
-
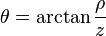 、
、
-
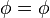 。
。
反过来,可以从圆柱坐标变换为球坐标:
-
 、
、
-
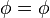 、
、
-
 。
。
标度因子[编辑]
球坐标系的标度因子分别为:
-
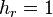 、
、
-
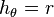 、
、
-
 。
。
无穷小体积元素是
-
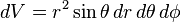 。
。
-
 。
。
其它微分算子,像  、
、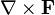 ,都可以用
,都可以用 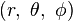 坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。
坐标表示,只要将标度因子代入在正交坐标系条目内对应的一般公式。
球坐标系下的积分和微分公式[编辑]
假定  是从原点到 P 点的连线与正 z-轴的夹角
是从原点到 P 点的连线与正 z-轴的夹角
- 线元素是一个从
 到
到  的无穷小位移,表示为公式:
的无穷小位移,表示为公式:
-
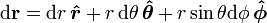 ;
;
其中的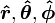 是在
是在 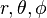 的各自的增加的方向上的单位矢量。
的各自的增加的方向上的单位矢量。
- 面积元素1:在球面上,固定半径,天顶角从
 到
到  ,方位角从
,方位角从  到
到  变化,公式为:
变化,公式为:
-
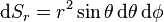 。
。
- 面积元素2:固定天顶角
 ,其他两个变量变化,则公式为:
,其他两个变量变化,则公式为:
-
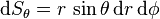 。
。
- 面积元素3:固定方位角
 ,其他两个变量变化,则公式为:
,其他两个变量变化,则公式为:
-
 。
。
- 体积元素,径向坐标从
 到
到 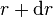 ,天顶角从
,天顶角从 到
到  ,并且方位角从
,并且方位角从  到
到  的公式为:
的公式为:
-
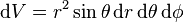 。
。
- 梯度公式:
-
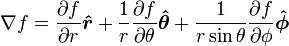 。
。
- 散度公式:
-
 。
。
- 旋度公式:
-
 。
。
-
 。
。
应用[编辑]
地理坐标系用两个角值,纬度与经度,来表示地球表面的地点。正如二维直角坐标系专精在平面上,二维球坐标系可以很简易的设定圆球表面上的点的位置。在这里,我们认定这圆球是个单位圆球;其半径是1。通常我们可以忽略这圆球的半径。在解析旋转矩阵问题上,这方法是非常有用的。
球坐标系适用于分析一个对称于点的系统。举例而言,一个圆球,其直角坐标方程式为 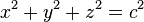 ,可以简易的用球坐标系
,可以简易的用球坐标系 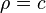 来表示。
来表示。
当求解三重积分时,如果定义域为圆球,则面积元素是
-
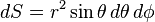 ;
;
体积元素是
-
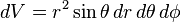 。
。
用来描述与分析拥有球状对称性质的物理问题,最自然的坐标系,莫非是球坐标系。例如,一个具有质量或电荷的圆球形位势场。两种重要的偏微分方程式, 拉普拉斯方程 与亥姆霍兹方程,在球坐标里,都可以成功的使用分离变量法求得解答。这种方程式在角部分的解答,皆呈球谐函数的形式。
球坐标的概念,延伸至高维空间,则称为超球坐标 (n-sphere) 。








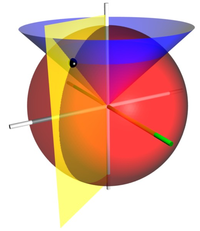
 。蓝色圆锥面的
。蓝色圆锥面的
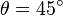 。黄色半平面的
。黄色半平面的
 (黄色半平面与 xz-半平面之间的
(黄色半平面与 xz-半平面之间的
 )。 z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个坐标曲面相交于点 P (以黑色的圆球表示)。
)。 z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个坐标曲面相交于点 P (以黑色的圆球表示)。
 。
。

















 2344
2344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








