目录
1.等电位点
⑴等电位,即等电势。如果两点间电位相等,电压为零,则这两点称为等电位点。
⑵分析电路时,根据参数(变量值)计算的需要,等电位点之间的支路,可以断开,也可以短路,不会影响电路的其余部分。
2.平衡电桥

图1
图1所示的惠通斯电桥,可将![]() 构成的∆形联结等效成如图2所示的Y形联结,
构成的∆形联结等效成如图2所示的Y形联结,![]() 时,很容易通过图2证明,ce和de两个支路的电压降相等,所以,图1中,对角线支路
时,很容易通过图2证明,ce和de两个支路的电压降相等,所以,图1中,对角线支路![]() 两端等电位,此时的电桥称为平衡电桥,
两端等电位,此时的电桥称为平衡电桥,![]() 可以去掉,也可以短路。
可以去掉,也可以短路。

图2
图1所示的惠通斯电桥,可将![]() 构成的∆形联结等效成如图2所示的Y形联结,
构成的∆形联结等效成如图2所示的Y形联结,![]() 时,很容易通过图2证明,ce和de两个支路的电压降相等,所以,图1中,对角线支路
时,很容易通过图2证明,ce和de两个支路的电压降相等,所以,图1中,对角线支路![]() 两端等电位,此时的电桥称为平衡电桥,
两端等电位,此时的电桥称为平衡电桥,![]() 可以去掉,也可以短路。
可以去掉,也可以短路。
题1电路如图3所示,求等效电阻![]() 。
。

图3
解析:原电路是一个平衡电桥(将图3变形为图4看得更清楚),故
![]()

图4
题2电路如图5所示,求电压源和电流源功率。

图5
解析:原电路5Ω右侧为平衡电桥(图5虚线圈内所示),可断开30Ω支路,则电压源右侧电路的等效电阻为
![]()
因此,电路简化为如图6所示。

图6
则![]() ;
;
![]() ;
;
![]() (发出300W功率);
(发出300W功率);
![]() (吸收100W功率)。
(吸收100W功率)。
3.对称(平衡)网络
类似于平衡电桥,具有对称性的特殊复杂网络,可利用其对称性寻找等电位点,进而通过短接等电位点或断开所连接支路,简化电路分析和变量计算。
对称的类型一般包括立体网络的传递面对称(传递面两侧对称点等电位)和平面平衡网络的轴线对称(轴线两侧对称点等电位)。
题3求图7所示电路a、h端的等效电阻![]() ,设图中所有电阻都是1Ω。
,设图中所有电阻都是1Ω。

图7
解析:对端口ah,有achf和adhg两个传递对称面,因此b、d、f三点等电位,c、g、e也是等电位点,分别将它们短路,得等效电路如图8所示。

图8
所以,等效电阻

题4图9所示电路中,![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和 ![]() 。
。
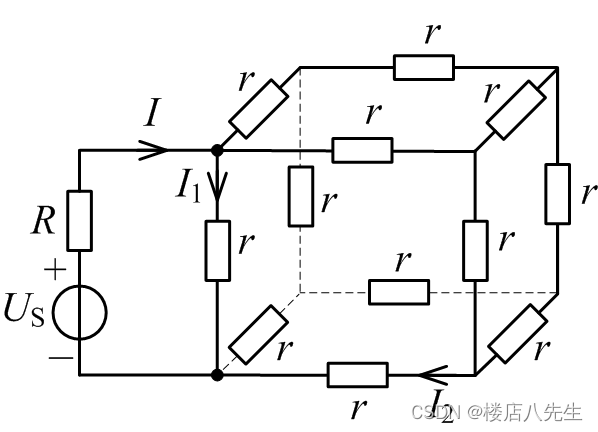
图9
解析:标注立方体电阻网络各结点如图10所示,对端口af,平面achf是其传递对称面,所以b、d等电位,e、g等电位,将它们分别短接,可得端口af的等效电阻为

图10

计算总电流和支路电流分别为


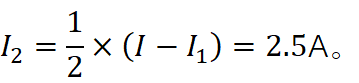








 本文详细介绍了等电位点的概念及其在电路分析中的应用,探讨了平衡电桥的工作原理以及如何通过等电位简化电路。同时,讨论了对称网络,特别是传递对称和平面平衡网络在求解等效电阻和功率问题中的作用。
本文详细介绍了等电位点的概念及其在电路分析中的应用,探讨了平衡电桥的工作原理以及如何通过等电位简化电路。同时,讨论了对称网络,特别是传递对称和平面平衡网络在求解等效电阻和功率问题中的作用。

















 2522
2522

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








