相机标定详解：从针孔模型到张正友方法-CSDN博客

本文链接：https://blog.csdn.net/hshagahhva/article/details/125366499

本文深入探讨了相机标定的重要性，从针孔相机模型开始，介绍了相机标定的基本概念、传统方法以及张正友标定法。详细阐述了相机标定的步骤，包括打印棋盘格、拍摄不同角度照片、提取角点、参数估计以及畸变校正。通过实验测试确保标定的准确性和精度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一：针孔相机模型

在针孔照相机模型中，在光线投影到图像平面之前，从唯一一个点经过，也就是照相机中心 C。根据相似三角形可以得出P点坐标和在投影面上坐标的关系

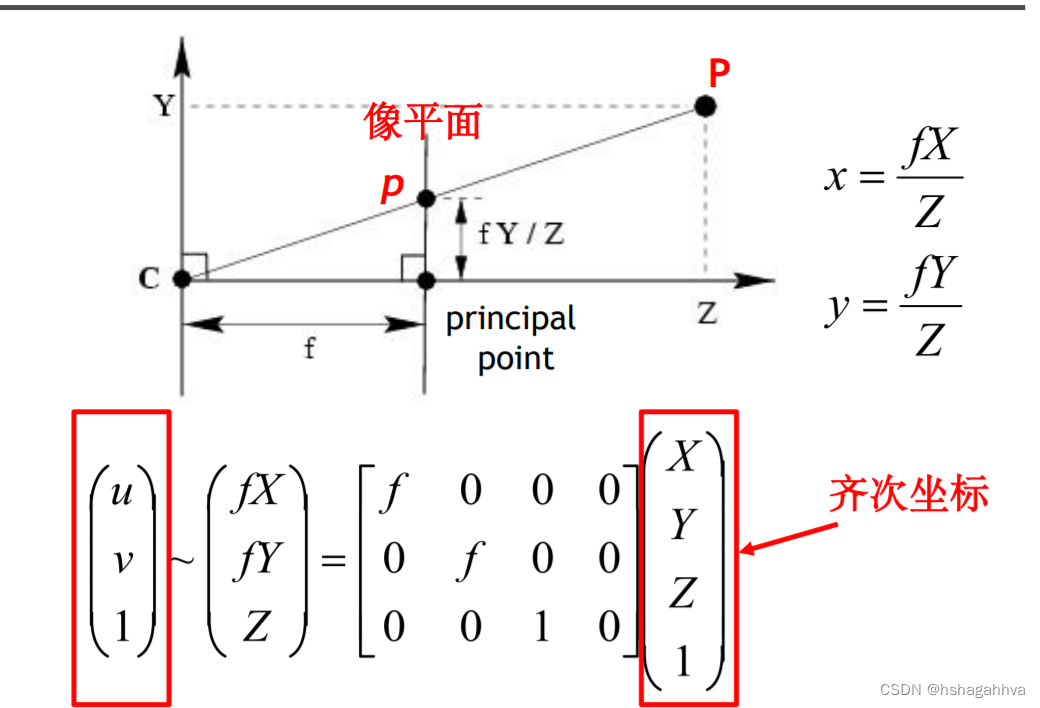
将坐标系改到像平面左下角时可以得到以下数据

照相机可以分解成如下图所示，我们需要恢复内参数K和照相机的位置t和姿势R，矩阵分块操作成为因子分解。我们将使用RQ因子分解来进行矩阵因子分解。

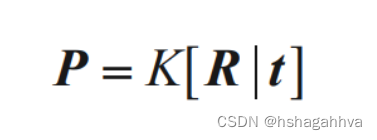
from numpy import array, dot, hstack

import camera

K = array([[1000,0,500],[0,1000,300],[0,0,1]])
tmp = camera.rotation_matrix([0,0,1])[:3,:3]
Rt = hstack((tmp,array([[50],[40],[30]])))
cam = camera.Camera(dot(K,Rt))

print(K,Rt)
print(cam.factor())