IEEE754浮点数的加减运算

最新推荐文章于 2025-03-10 06:30:00 发布

爱漂流的易子

最新推荐文章于 2025-03-10 06:30:00 发布

阅读量1.6k

点赞数 11

文章标签： fpga开发浮点数 IEEE754

本文链接：https://blog.csdn.net/hy_520520/article/details/143304027

版权

参考：IEEE754

浮点数的运算

IEEE754中规定了浮点数的基本运算。这些运算包括：加法，减法，乘法，除法，平方根，取余，向浮点格式整数舍入，不同浮点格式直接的转换，整形与浮点数之间的转换，二进制与十进制之间的转换，以及比较等运算。除了二进制与十进制之间的转换之外，其他运算要求先产生一个具有无限精度的中间值结果，再将该结果强制转换成目标格式。

浮点数的加法减法

对于两个操作数，a和b，对于a-b=a+(-b)。由此可见，减去一个数相当于加上这个数的相反数，反之亦然。故加法与减法在算法实现上时等价的。在进行浮点数的加减运算之前，必须使其指数相等，再对尾数进行相应的加减。这需要先判断操作数中的较大者和较小者，求出较大者与较小者的指数之差N，再将较小者的尾数右移N位，然后再对操作数的尾数进行相应的加减操作。

浮点数的舍入

在进行数值计算时，由于精度限制，需要保存的数字位数超过系统可以保存的位数时，不可避免的要对数值进行近似。在这个近似的过程中，就会涉及数值舍入规则的问题。IEEE754标准规定了浮点数的四种舍入规则，分别是：向最近的偶数舍入、向零舍入、向正无穷舍入和向负无穷舍入。

向最近的偶数舍入

向最近的偶数舍入，是IEEE754-标准规定的默认舍入模式。在这种舍入模式下，取与该数差值（绝对值）最小的数作为舍入结果，这个结果在数轴上与该数距离最近。如果与该数插值最小的数有两个，则取其中的偶数作为舍入结果。向最近的偶数舍入带来的舍入误差总是最小的，这也是它被规定位默认的舍入模式的原因。

向零舍入

直接将多余的位数舍去，在向零舍入模式下，正数舍入后的值不大于原理的值，负数舍入后的值不小于原理的值。

正无穷大舍入

在不小于该数的数中，取与该数差值最小的数作为舍入结果。这个结果在数轴的正无穷方向上与该数距离最近。在向正无穷舍入模式下，舍入后的值一定不小于原来的值。

向负无穷大舍入

在不大于该数的数中，取与该数差值最小的数作为舍入结果。这个结果在数轴的负无穷方向上与该数距离最近。在向负无穷舍入模式下，舍入后的值一定不大于原来的值。

浮点加减法运算原理

运算步骤：

计算指数差值。要进行加减运算必须使操作数的指数相等，通过计算指数的差值diff可以判断操作数指数是否相等。如果不相等则需要在下一步中进行尾数移位以使指数相等，如果相等则不需要移位。
尾数移位。对指数较小的操作数的尾数向右移位，若尾数右移1位则指数加1，指数差值为diff，故需要尾数右移diff位。
尾数加减，指数相等的浮点数进行加减，指数保持原来的值不变，对应的尾数进行加减，这一步是整数加减运算。
尾数规格化。尾数计算结果的格式可能不符合浮点标准。比如：规格化浮点数的尾数最高位为1，而计算结果不一定最高位为1。故需要对尾数进行移位，同时对指数进行必要的加减。

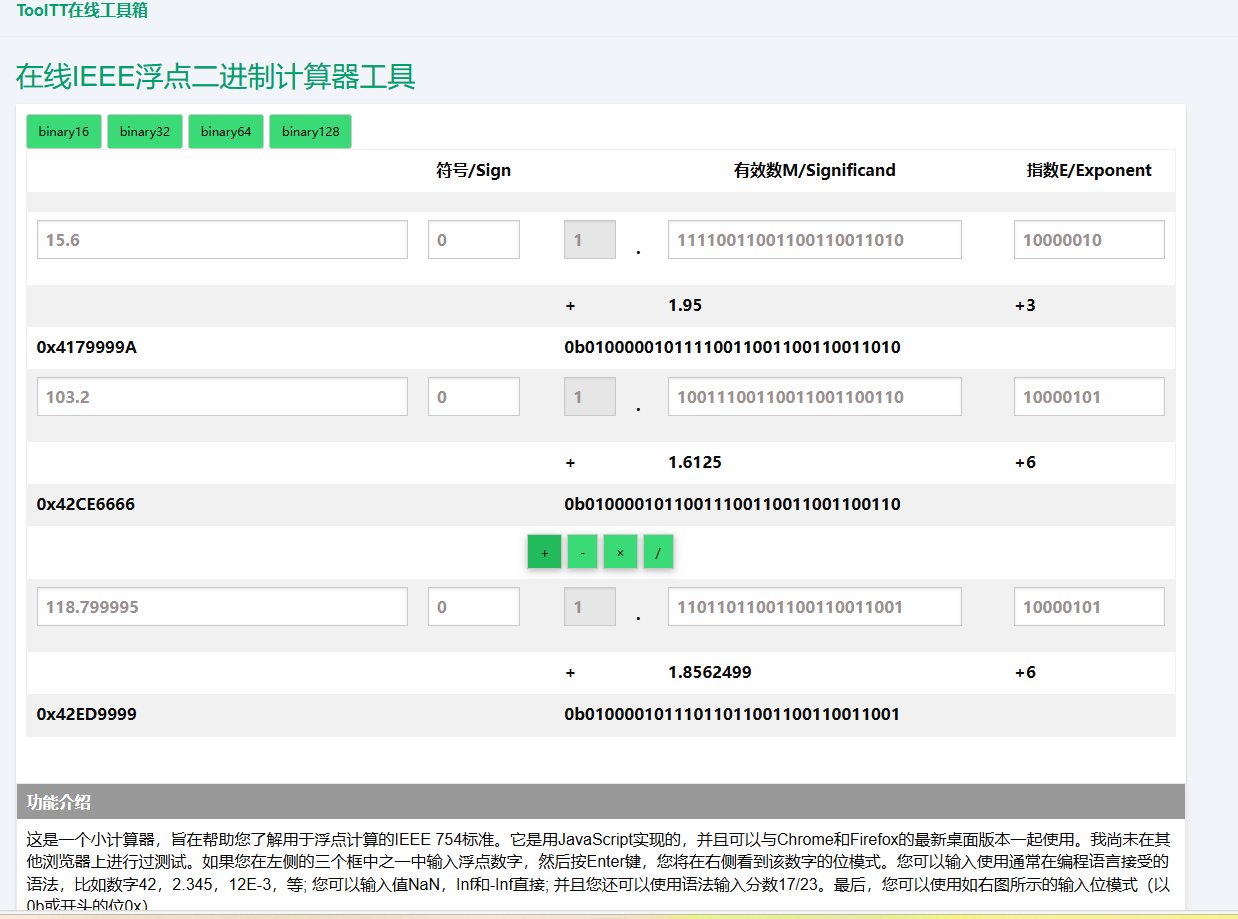
加法运算

例如两个浮点数

十进制数	单精度浮点数	符号位	阶码	尾数
A=15.6	32‘h4179_999a	1’b0	8‘b10000010	24’b111110011001100110011010
B=103.2	32‘h42ce_6666	1’b0	8’b10000101	24’b110011100110011001100110
A+B=118.8	32‘h42ed_999a	1’b0	8’b10000101	24’b111011011001100110011010

现在按照上面说的步骤进行运算。

计算指数差值。

EA=8‘b10000010；

EB=8’ b10000101

判断两个数据指数的大小

EA<EB

计算两个指数差值

Diff=EB-EA=8‘b0000_0011，用十进制数表示为(3)10。阶码差值为3。

尾数位移。

将指数较小的操作数尾数向右移动一位，同时指数加一，直到指数相等。MA尾数右移三位为24’b000111110011001100110011，EA加3为8‘b10000101。

尾数加减

经过尾数位移后的尾数为。

MA=24’b000011110011001100110011

MB=24’b110011100110011001100110

MC=MB+MA=24‘b111011011001100110011001

符号判断

EB>EA，SC与SB同号=1‘b0。

尾数规格化。

结果尾数最高位为1，不需要规格化。

所以结果

SC=1‘b0

EC=8’b10000101

MC=24‘b111011011001100110011001

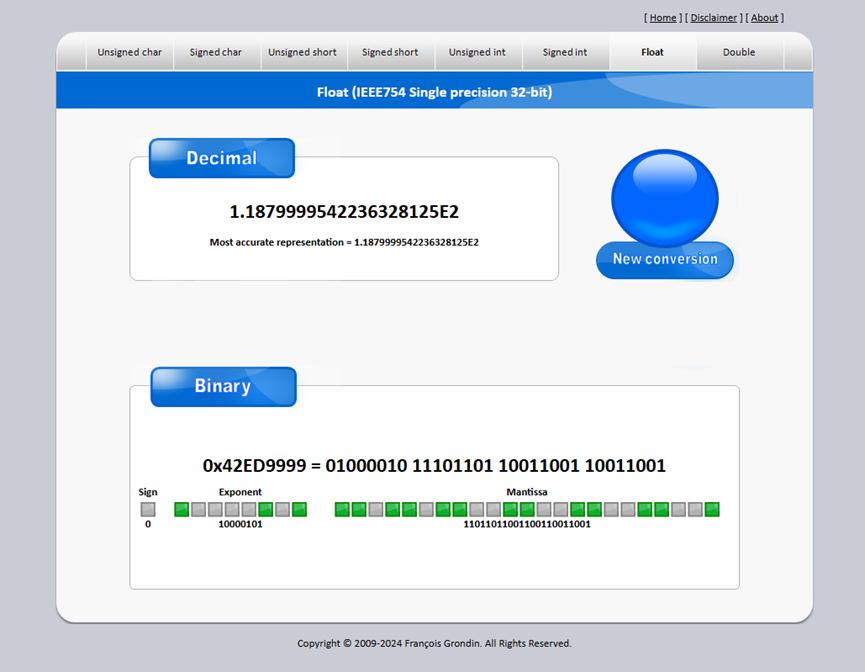
上述结果转为为32位浮点数为0x42ed_9999，而A+B=118.8，转换为浮点数为0x42ed_999a。

可以发现他们精度不同。这是由于我们舍入方式不同。

减法运算

例如两个浮点数

十进制数	单精度浮点数	符号位	阶码	尾数
A=15.6	32’h4179_999a	1’b0	8‘b10000010	24’b111110011001100110011010
B=103.2	32’h42ce_6666	1’b0	8’b10000101	24’b110011100110011001100110
A-B=-87.6	32‘hc2af_3333	1’b1	8’b10000101	24’b101011110011001100110011