Unity Shader数学基础

目录

一、三维笛卡尔坐标系

1.1 左右手坐标系判断

1.2 左右手坐标系旋转正方向判断

1.3 其它

二、点和矢量

三、矢量运算

3.1 矢量和标量的乘/除法

3.2 矢量的加减法

3.3 矢量的模

3.4 单位矢量

3.5 矢量的点积（内积）—  标量

3.5.1 代数角度：

3.5.2 几何角度：

3.5.3 两矢量方向判定

3.5.4 点积的性质

3.6 矢量的叉积（外积）—  向量

3.6.1 叉积的计算

3.6.2 叉积的用处

---

声明：部分摘抄自维基百科。

 

一、三维笛卡尔坐标系

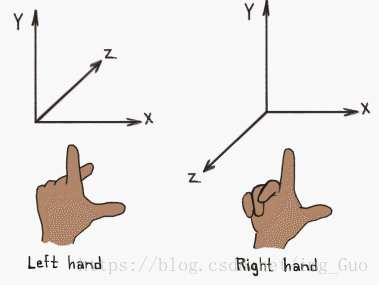
所有二维笛卡尔坐标系都是等价的（可以通过旋转进行统一），但是三维笛卡尔坐标系并不都是等价的。如果两个坐标系具有相同的旋向性，那么我们就可以通过旋转的方法让两个坐标轴指向重合，但是如果它们不具备相同的旋向性，那么我们就不可以通过单纯的旋转的方法来让它们重合（如 左手坐标系和右手坐标系）。

1.1 左右手坐标系判断

除了用左右手判断以外，还可以判断前向(forward)：

坐直，右面的方向时X轴方向，头顶方向时Y轴方向，如果正前方时Z轴正方向，那就是左手坐标系；如果正前方是Z轴负方向，那就是右手坐标系。

左右手坐标系（Ref： 网站链接）

1.2 左右手坐标系旋转正方向判断

左手坐标系旋转正方向由左手法则定义，右手坐标系旋转正方由右手法则定义。

1. 左手法则：伸出左手，握拳，伸出大拇指让它指向旋转轴正方向，那么四个手指弯曲方向为旋转正方向（顺时针方向）。

2. 右手法则：伸出右手，握拳，伸出大拇指让它指向旋转轴正方向，那么四个手指弯曲方向为旋转正方向（逆时针方向）。

1.3 其它

1. 左右手坐标系是可以相互转换的，最简单的方法是保持两个坐标轴不变，把其中一个轴反转。注意，在左手坐标系和右手坐标系中，相同的点运动轨迹，两个坐标系之间的数学描述不同。想要在两个坐标系之间进行变换，参见《Conversion of Left-Handed Coordinates to Right-Handed Coordinates》。

2. Unity使用的坐标系

对于世界空间和模型空间：Unity使用左手坐标系；

对于观察空间（以摄像机为原点的坐标空间）：右手坐标系，摄像机前向是Z轴的负方向、Z轴值越小，物体的深度越大，离摄像机越远。

 

二、点和矢量

1. 点是n维空间中的一个位置，没有大小、宽度等概念，在笛卡尔坐标系中可以使用2个或者3个实数来表示一个点的坐标；

2. 矢量是n维空间中一种包含了模和方向的有向线段，矢量没有位置；

3. 通常，矢量被用于表示相对于某个点的偏移，也就是说是一个相对量，只要知道矢量端点（尾或头）的一个位置，就可以知道矢量另一个端点（头或尾）代表的位置了。只要矢量的模和方向保持不变，无论放在哪里都是同一个矢量。

 

 

三、矢量运算

3.1 矢量和标量的乘/除法

公式很简单，只需要把矢量的每一个分量和标量相乘/除即可。

3.2 矢量的加减法

计算只需要把两个矢量对应分量进行相加减即可，对应的几何层次上的法则是三角形定则。

 

PS：图形学中要时刻谨记，图形学中矢量通常用于描述偏移（简称位移）。因此我们可以利用数量的加减法来计算一点相对于另一点的位移。例如，假设空间中有两点a和b，我们可以用矢量a和b表示它们相对于原点的位移，如果我们想要计算点b相对于点a的位移，我们可以通过b-a得到。

3.3 矢量的模

矢量的模是一个标量，可以理解为矢量在空间中的长度。各个维度矢量模的计算都是类似的，都是对每个分量的平方相加后再开根号得到。

还有一种方法可以求一个矢量的模，可以利用矢量与自身的点积结果开平方。

3.4 单位矢量

很多情况下，我们只关注矢量的方向而不是模，在这种情况下我们就需要使用单位矢量。比如说计算光照模型时候，我们往往需要得到顶点的法线方向和光源方向，此时我们不关注矢量有多长。

单位矢量：模为1的矢量；

归一化矢量：对任何给定的非零矢量，把它转换成单位矢量的过程就被称为归一化，计算公式为矢量除以矢量的模。其中，零矢量不能被归一化，因为除法运算分母不能为0。

3.5 矢量的点积（内积）—  标量

从代数角度看，先对两个数字序列中的每组对应元素求积，再对所有积求和，结果即为点积。从几何角度看，点积则是两个向量的长度与它们夹角余弦的积（也就是投影）。这两种定义在笛卡尔坐标系中等价。

3.5.1 代数角度：

3.5.2 几何角度：

几何角度下的点积意义很重要，其中一个比较重要的意义就是投影。

这样，两个互相垂直的向量的点积总是零。若两个向量都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。倘若任意给定两个向量，它们之间的夹角可以通过下列公式得到：

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

例如：假设有一个单位矢量a和另一个长度不限的矢量b，现在我们希望得到b在平行于a的一条直线上的投影。那么我们就可以使用点积来表示b在a方向上的影子。

3.5.3 两矢量方向判定

点积结果的符号可以判定两个矢量间的关系。方向相反，点积小于0；方向垂直，点积等于0；方向相同，点积大于0。

3.5.4 点积的性质

1、 满足交换律

2、 满足分配律（即点积可以结合矢量加减法）

3、 点积可结合标量乘法

也就是说，对点积中其中一个矢量进行缩放的结果，相当于对最后的点积结果进行缩放。

4、 矢量与本身进行点积的结果，是该矢量模的平方

这个性质的第一点就是可以不用求模公式求矢量的模，当然，更重要的一点是当我们想要比较两个矢量模（长度）的大小，我们可以直接比较点积的结果。

 

3.6 矢量的叉积（外积）—  向量

与点积不同，它的运算结果是向量。对于线性无关的两个向量  和  ，它们的叉积写作 ，是 和 所在平面的法线向量，与 和 都垂直。

如果两个向量方向相同或相反（即它们非线性无关），亦或任意一个的长度为零，那么它们的叉积为零向量。推广开来，叉积的模长和以这两个向量为边的平行四边形的面积相等；如果两个向量成直角，它们叉积的模长即为两者长度的乘积。

3.6.1 叉积的计算

1、 模长：

2.、方向：左手坐标系用左手判断，右手坐标系用右手判断。

【举例】假设两个矢量  、 不互相垂直，则可将右手掌张开，将四根手指朝着 的方向指去，然后将大拇指伸开垂直于四根手指，再找到这四根手指与 之间角度最小的夹角，将这四根手指弯扫过这夹角，则 的方向是大拇指所指的方向。

3.6.2 叉积的用处

最常见的用处就是计算垂直于一个平面、三角形的矢量。另外，还可以判断三角面片的朝向。