首先引入一个具有子晶格对称性的玩具模型:
(00tx+teikxty+t⋅eiky00−ty−t⋅e−ikytx+t⋅e−ikxtx+t⋅e−ikx−ty−t⋅eiky00ty+t⋅e−ikytx+t⋅eikx00)\large\left(\begin{array}{cccc} 0 & 0 & t_{x}+t e^{i k_{x}} & t_{y}+t \cdot e^{i k_{y}} \\ 0 & 0 & -t_{y}-t \cdot e^{-i k_{y}} & t_{x}+t \cdot e^{-i k_{x}} \\ t_{x}+t \cdot e^{-i k_{x}} & -t_{y}-t \cdot e^{i k_{y}} & 0 & 0 \\ t_{y}+t \cdot e^{-i k_{y}} & t_{x}+t \cdot e^{i k_{x}} & 0 & 0 \end{array}\right)00tx+t⋅e−ikxty+t⋅e−iky00−ty−t⋅eikytx+t⋅eikxtx+teikx−ty−t⋅e−iky00ty+t⋅eikytx+t⋅e−ikx00
ref:DOI: 10.1103/PhysRevLett.125.166801
注意这是哈密顿量的核,具有Mx My reflection symmetries
单个原胞的原子顺序:
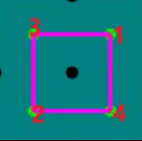
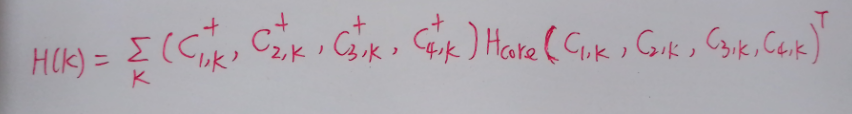
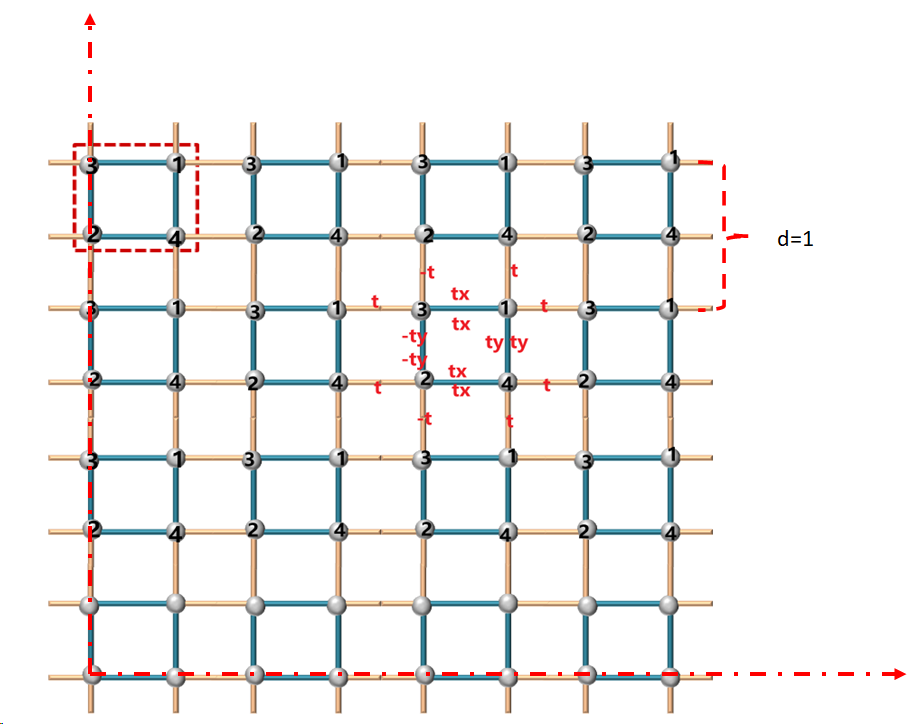
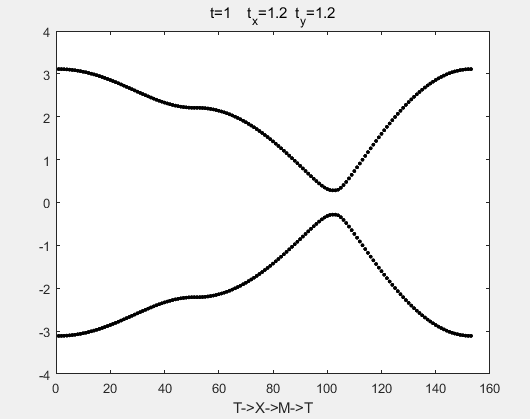
周期结构的能带
function []=BandMian()
clear;clc;close all
global t tx ty d
d=1;%晶格常数
t=1;
tx=1;
ty=1;
kx_ky0=BZ_dispersed();
num_kxky=length(kx_ky0);
STO=zeros(4,num_kxky);
for uu=1:num_kxky
uu/num_kxky
kx=real(kx_ky0(uu));
ky=imag(kx_ky0(uu));
[vec,val]=eig(Hami(kx,ky));
val=sort(diag(val));
STO(:,uu)=val;
end
plot(1:num_kxky,STO,'k.','MarkerSize',10)
title(['t=',num2str(t),' t_x=',num2str(tx),' t_y=',num2str(ty)])
xlabel('T->X->M->T')
end
function [op]=Hami(kx,ky)
global t tx ty
H0=sym(zeros(2,2));
H0(1,1)=tx+t*exp(1j*kx);
H0(1,2)=ty+t*exp(1j*ky);
H0(2,1)=-ty-t*exp(-1j*ky);
H0(2,2)=tx+t*exp(-1j*kx);
op=[sym(zeros(2,2)),H0;H0',sym(zeros(2,2))];
end
function [k0]=BZ_dispersed()
global d
%d晶格常数
%a=1;%临时参数
%T->X->M->T
delta=0.02;%可调参数
T=[0,0];
M=(pi/d)*[1,1];
X=(pi/d)*[1,0];
MT=T-M;
mt=MT(1)+MT(2)*1i;
list_mt=(M(1)+M(2)*1i)+[0:delta:1]*mt;
TX=X-T;
tx=TX(1)+TX(2)*1i;
list_tx=(T(1)+T(2)*1i)+[0:delta:1]*tx;
XM=M-X;
xm=XM(1)+XM(2)*1i;
list_xm=(X(1)+X(2)*1i)+[0:delta:1]*xm;
k0=[list_tx,list_xm,list_mt];
end
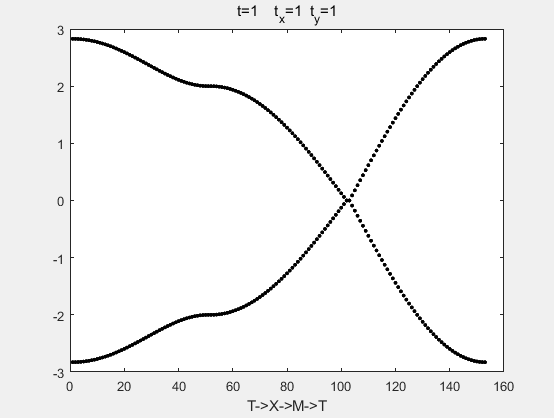
这是均匀格子的。
实空间中哈密顿量的构建
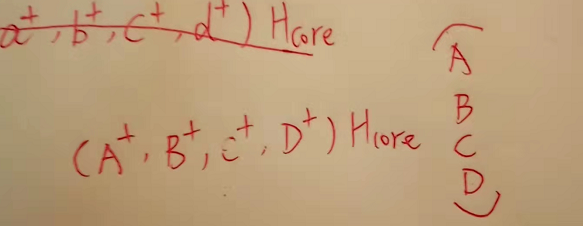
其中:
Hcore =(00txty00−tytxtx−ty00tytx00)\Large H_{\text {core }}=\left(\begin{array}{cccc}
0 & 0 & t_{x} & t_{y} \\
0 & 0 & -t_{y} & t_{x} \\
t_{x} & -t_{y} & 0 & 0 \\
t_{y} & t_{x} & 0 & 0
\end{array}\right)Hcore =00txty00−tytxtx−ty00tytx00
这都是一个原胞内的跳跃
有限结构的能带图和角态
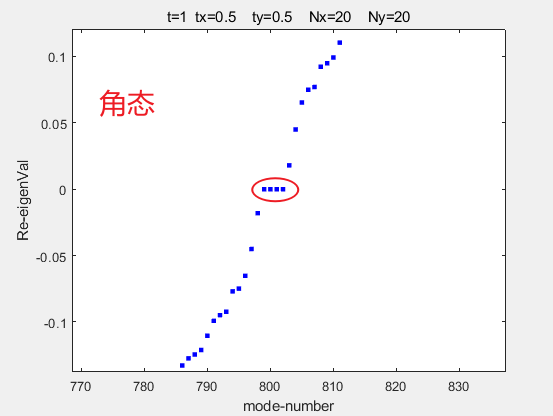
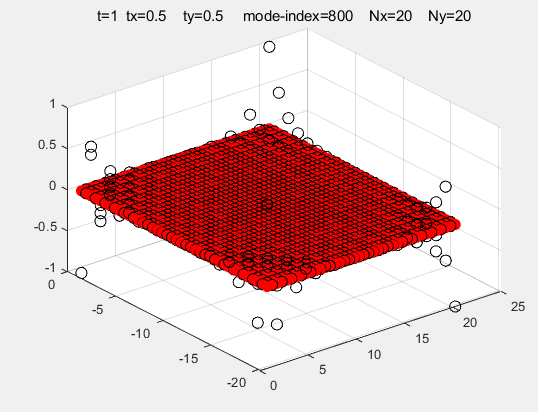
绘制代码:
function []=RealSpaceQxy_2DSSH()
clear;clc;
global Nx Ny
Nx=20;%x向原胞数,一个原胞四个原子
Ny=20;%y向原胞数,一个原胞四个原子
d=1;%晶格常数
t=1;
tx=0.5;
ty=0.5;
len=0.5*d;
a1=[d,0];
a2=[0,-d];
para0=0;%为0开启能带图绘制
para=0;%为0开启波函数绘制
%mode_index=2;%按照特征值实部从小到大的索引
if para0==0
delete('sort_vec.mat');
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[sortRe_val,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
save('sort_vec.mat','sort_vec');
figure(1)
plot(1:length(sortRe_val),sortRe_val,'b.','MarkerSize',10)
xlabel('mode-number')
ylabel('Re-eigenVal')
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para==0
sort_vec=cell2mat(struct2cell(load('sort_vec.mat')));%加载要处理的数据
mode_index=input('请输入模式索引:');
choice_wave=sort_vec(:,mode_index);%列向量
choice_wave=choice_wave./max(abs(real(choice_wave)));%归一化
num_sto=[4:4:length(choice_wave)];%序号
STO=[];
for ii=1:Ny
for jj=1:Nx
center=ii*a2+jj*a1;
h_index=(ii-1)*Nx+jj;
num2=num_sto(h_index);
num1=num2-3;
op=ProductFourPoint(center,len);
v0=choice_wave(num1:num2);
STO=[STO;op,v0];
end
end
figure(2)
scatter3(STO(:,1),STO(:,2),zeros(length(choice_wave),1),70,'ro','filled')
hold on
scatter3(STO(:,1),STO(:,2),real(STO(:,3)),70,'ko')
hold off
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),...
' mode-index=',num2str(mode_index),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
delete('sort_vec.mat');
end
end
function [op]=FinalSize_Hami(t,tx,ty)
global Nx Ny
%Nx=1;%x向原胞数
%Ny=2;%y向原胞数
H0=zeros(4,4);
H0(1,3)=tx;
H0(1,4)=ty;
H0(2,3)=-ty;
H0(2,4)=tx;
H0(3,1)=tx;
H0(3,2)=-ty;
H0(4,1)=ty;
H0(4,2)=tx;
H1=zeros(4,4);
H1(1,3)=t;
H1(4,2)=t;
H1T=H1.';%纯转置
H2=zeros(4,4);
H2(1,4)=-t;
H2(3,2)=-t;
H2T=H2.';%纯转置
vec_len=Nx*Ny;
HH0=kron(diag(ones(1,vec_len)),H0);
one_sto=[];
for ii=1:vec_len-1
if ii/Nx==fix(ii/Nx)%整数
one_sto=[one_sto,0];
else
one_sto=[one_sto,1];
end
end
HH1=kron(diag(one_sto,1),H1)+kron(diag(one_sto,-1),H1T);
HH2=kron(diag(ones(1,vec_len-Nx),-Nx),H2)+...
kron(diag(ones(1,vec_len-Nx),Nx),H2T);
op=HH0+HH1+HH2;%总的哈密顿量
end
function [op]=ProductFourPoint(center,len)
%输入中心center坐标[x,y]和一个原胞中四个原子的相邻两两距离len(晶格常数的倍数)
%输出的是[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意我认为:
% 3————1
% | |
% | |
% 2————4
%
xc=center(1);
yc=center(2);
L=0.5*len;
x1=xc+L;y1=yc+L;
x2=xc-L;y2=yc-L;
x3=xc-L;y3=yc+L;
x4=xc+L;y4=yc-L;
op=[x1,y1;...
x2,y2;...
x3,y3;...
x4,y4];
end
算体四极矩(实空间法)
算出的波函数形式:(u11;u12;u13;u14;u21;u22;u23;u24;u31;u32;u33;u34...)\Large (u11;u12;u13;u14;u21;u22;u23;u24;u31;u32;u33;u34...)(u11;u12;u13;u14;u21;u22;u23;u24;u31;u32;u33;u34...)(假设Nx=Ny=4),其中u=(c1;c2;c3;c4)\Large u=(c1;c2;c3;c4)u=(c1;c2;c3;c4)。都是列向量
成功的代码:
function []=RealSpaceQxy_2DSSH()
clear;clc;
global Nx Ny d
Nx=20;%x向原胞数,一个原胞四个原子
Ny=20;%y向原胞数,一个原胞四个原子
d=1;%晶格常数
t=1;
tx=1;
ty=1;
len=0.5*d;
a1=[d,0];%正空间基矢
a2=[0,-d];%倒空间基矢
para0=0;%为0开启能带图绘制和开启Qxy的计算
para=1;%为0开启波函数绘制
%mode_index=2;%按照特征值实部从小到大的索引
if para0==0
delete('sort_vec.mat');
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[sortRe_val,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
save('sort_vec.mat','sort_vec');
figure(1)
plot(1:length(sortRe_val),sortRe_val,'b.','MarkerSize',10)
xlabel('mode-number')
ylabel('Re-eigenVal')
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para0==0
intercellX=d/(abs(tx/t)+1);%原胞之间边长的距离,x向
incellX=d-intercellX;%原胞内边长的距离,x向
intercellY=d/(abs(ty)/abs(t)+1);%原胞之间边长的距离,y向
incellY=d-intercellY;%原胞内边长的距离,y向
Lx=(Nx-1)*d+incellX;%有限结构x向边长
Ly=(Ny-1)*d+incellY;%有限结构x向边长
Cell_index=[];%原胞索引(一个原胞四个原子)
for uu=1:Ny
for vv=1:Nx
Cell_index=[Cell_index;uu,vv];
end
end
num2=[4:4:Nx*Ny*4];%序号
num1=num2-3;
StoSite=zeros(Nx*Ny*4,2);%第一二列是xy实际坐标,和列波函数的顺序是完全对应的
for zz=1:length(Cell_index)
n1=num1(zz);
n2=num2(zz);
Site4=FourIndex(Cell_index(zz,1:2),incellX,incellY);
StoSite(n1:n2,1:2)=[Site4];
end
xy=StoSite(:,1).*StoSite(:,2);%xy算符结果,列向量
xy=exp(xy./(Lx*Ly).*(2*pi*1j));%列向量
Q=diag(xy);
lie=size(sort_vec,2);
U=sort_vec(:,1:lie/2);%选择Re(E)<0的波函数,选择一半
%U=sort_vec(:,lie/2+1:end);%一个怪异的选择
S=U'*Q*U;
Qxy=angle(det(S)*sqrt(det(Q')))/(2*pi);
disp(['Real_Space_Qxy=',num2str(Qxy)]);
end
if para==0
sort_vec=cell2mat(struct2cell(load('sort_vec.mat')));%加载要处理的数据
mode_index=input('请输入模式索引:');
choice_wave=sort_vec(:,mode_index);%列向量
choice_wave=choice_wave./max(abs(real(choice_wave)));%归一化
num_sto=[4:4:length(choice_wave)];%序号
STO=[];
for ii=1:Ny
for jj=1:Nx
center=ii*a2+jj*a1;
h_index=(ii-1)*Nx+jj;
num2=num_sto(h_index);
num1=num2-3;
op=ProductFourPoint(center,len);
v0=choice_wave(num1:num2);
STO=[STO;op,v0];
end
end
figure(2)
scatter3(STO(:,1),STO(:,2),zeros(length(choice_wave),1),70,'ro','filled')
hold on
scatter3(STO(:,1),STO(:,2),real(STO(:,3)),70,'ko')
hold off
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),...
' mode-index=',num2str(mode_index),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
end
function [op]=FinalSize_Hami(t,tx,ty)
global Nx Ny
%Nx=1;%x向原胞数
%Ny=2;%y向原胞数
H0=zeros(4,4);
H0(1,3)=tx;
H0(1,4)=ty;
H0(2,3)=-ty;
H0(2,4)=tx;
H0(3,1)=tx;
H0(3,2)=-ty;
H0(4,1)=ty;
H0(4,2)=tx;
H1=zeros(4,4);
H1(1,3)=t;
H1(4,2)=t;
H1T=H1.';%纯转置
H2=zeros(4,4);
H2(1,4)=-t;
H2(3,2)=-t;
H2T=H2.';%纯转置
vec_len=Nx*Ny;
HH0=kron(diag(ones(1,vec_len)),H0);
one_sto=[];
for ii=1:vec_len-1
if ii/Nx==fix(ii/Nx)%整数
one_sto=[one_sto,0];
else
one_sto=[one_sto,1];
end
end
HH1=kron(diag(one_sto,1),H1)+kron(diag(one_sto,-1),H1T);
HH2=kron(diag(ones(1,vec_len-Nx),-Nx),H2)+...
kron(diag(ones(1,vec_len-Nx),Nx),H2T);
op=HH0+HH1+HH2;%总的哈密顿量
end
function [op]=ProductFourPoint(center,len)
%输入中心center坐标[x,y]和一个原胞中四个原子的相邻两两距离len(晶格常数的倍数)
%输出的是[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意我认为:
% 3————1
% | |
% | |
% 2————4
%
xc=center(1);
yc=center(2);
L=0.5*len;
x1=xc+L;y1=yc+L;
x2=xc-L;y2=yc-L;
x3=xc-L;y3=yc+L;
x4=xc+L;y4=yc-L;
op=[x1,y1;...
x2,y2;...
x3,y3;...
x4,y4];
end
function [opp]=FourIndex(c_index,incellX,incellY)%输入原胞索引和胞内胞间边长,输出一个原胞内四个原子的坐标
global d
%原胞索引形式为:[a,b]
%注意输出形式为:
%[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意坐标原点(0,0)是u11所处原胞的3号原子
aa=c_index(1);
bb=c_index(2);
x3=(bb-1)*d;
y3=-(aa-1)*d;
x1=x3+incellX;
y1=y3;
x2=x3;
y2=y3-incellY;
x4=x1;
y4=y2;
opp=[x1,y1;x2,y2;x3,y3;x4,y4];
end
Qxy相图,有正有负,不知道为何:
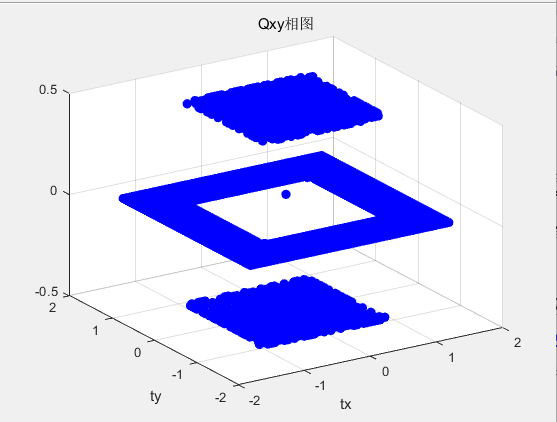
绘制代码(注意Qxy只能表征角态):
function []=RealSpaceQxy_2DSSH()
clear;%clc;
global Nx Ny d t
Nx=20;%x向原胞数,一个原胞四个原子
Ny=20;%y向原胞数,一个原胞四个原子
d=1;%晶格常数
t=1;
tx=1;
ty=1;
len=0.5*d;
a1=[d,0];%正空间基矢
a2=[0,-d];%倒空间基矢
para0=1;%为0开启能带图绘制和开启Qxy的计算
para=1;%为0开启波函数绘制
para2=0;%为0开启画相图
%mode_index=2;%按照特征值实部从小到大的索引
if para0==0
delete('sort_vec.mat');
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[sortRe_val,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
save('sort_vec.mat','sort_vec');
figure(1)
plot(1:length(sortRe_val),sortRe_val,'b.','MarkerSize',10)
xlabel('mode-number')
ylabel('Re-eigenVal')
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para0==0
intercellX=d/(abs(tx/t)+1);%原胞之间边长的距离,x向
incellX=d-intercellX;%原胞内边长的距离,x向
intercellY=d/(abs(ty)/abs(t)+1);%原胞之间边长的距离,y向
incellY=d-intercellY;%原胞内边长的距离,y向
Lx=(Nx-1)*d+incellX;%有限结构x向边长
Ly=(Ny-1)*d+incellY;%有限结构x向边长
Cell_index=[];%原胞索引(一个原胞四个原子)
for uu=1:Ny
for vv=1:Nx
Cell_index=[Cell_index;uu,vv];
end
end
num2=[4:4:Nx*Ny*4];%序号
num1=num2-3;
StoSite=zeros(Nx*Ny*4,2);%第一二列是xy实际坐标,和列波函数的顺序是完全对应的
for zz=1:length(Cell_index)
n1=num1(zz);
n2=num2(zz);
Site4=FourIndex(Cell_index(zz,1:2),incellX,incellY);
StoSite(n1:n2,1:2)=[Site4];
end
xy=StoSite(:,1).*StoSite(:,2);%xy算符结果,列向量
xy=exp(xy./(Lx*Ly).*(2*pi*1j));%列向量
Q=diag(xy);
lie=size(sort_vec,2);
U=sort_vec(:,1:lie/2);%选择Re(E)<0的波函数,选择一半
%U=sort_vec(:,lie/2+1:end);%一个怪异的选择
S=U'*Q*U;
Qxy=angle(det(S)*sqrt(det(Q')))/(2*pi);
disp(['Real_Space_Qxy=',num2str(Qxy)]);
end
if para==0
sort_vec=cell2mat(struct2cell(load('sort_vec.mat')));%加载要处理的数据
mode_index=input('请输入模式索引:');
choice_wave=sort_vec(:,mode_index);%列向量
choice_wave=choice_wave./max(abs(real(choice_wave)));%归一化
num_sto=[4:4:length(choice_wave)];%序号
STO=[];
for ii=1:Ny
for jj=1:Nx
center=ii*a2+jj*a1;
h_index=(ii-1)*Nx+jj;
num2=num_sto(h_index);
num1=num2-3;
op=ProductFourPoint(center,len);
v0=choice_wave(num1:num2);
STO=[STO;op,v0];
end
end
figure(2)
scatter3(STO(:,1),STO(:,2),zeros(length(choice_wave),1),70,'ro','filled')
hold on
scatter3(STO(:,1),STO(:,2),real(STO(:,3)),70,'ko')
hold off
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),...
' mode-index=',num2str(mode_index),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para2==0
PhaseDraw();
end
end%似乎只能表征角态
function []=PhaseDraw()
global Nx Ny d t
delta=0.05;
tx0=-1.5:delta:1.5;
ty0=tx0;
length_txy=length(tx0);
PhaseSto=zeros(length_txy^2,3);%一二列tx ty值,第三列Qxy值
count=0;
for ii=1:length_txy
mark=ii/length_txy
t1=clock;
for jj=1:length_txy
count=count+1;
tx=tx0(ii);
ty=ty0(jj);
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[~,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
intercellX=d/(abs(tx/t)+1);%原胞之间边长的距离,x向
incellX=d-intercellX;%原胞内边长的距离,x向
intercellY=d/(abs(ty)/abs(t)+1);%原胞之间边长的距离,y向
incellY=d-intercellY;%原胞内边长的距离,y向
Lx=(Nx-1)*d+incellX;%有限结构x向边长
Ly=(Ny-1)*d+incellY;%有限结构x向边长
Cell_index=[];%原胞索引(一个原胞四个原子)
for uu=1:Ny
for vv=1:Nx
Cell_index=[Cell_index;uu,vv];
end
end
num2=[4:4:Nx*Ny*4];%序号
num1=num2-3;
StoSite=zeros(Nx*Ny*4,2);%第一二列是xy实际坐标,和列波函数的顺序是完全对应的
for zz=1:length(Cell_index)
n1=num1(zz);
n2=num2(zz);
Site4=FourIndex(Cell_index(zz,1:2),incellX,incellY);
StoSite(n1:n2,1:2)=[Site4];
end
xy=StoSite(:,1).*StoSite(:,2);%xy算符结果,列向量
xy=exp(xy./(Lx*Ly).*(2*pi*1j));%列向量
Q=diag(xy);
lie=size(sort_vec,2);
U=sort_vec(:,1:lie/2);%选择Re(E)<0的波函数,选择一半
%U=sort_vec(:,lie/2+1:end);%一个怪异的选择
S=U'*Q*U;
Qxy=angle(det(S)*sqrt(det(Q')))/(2*pi);
PhaseSto(count,1:3)=[tx,ty,Qxy];
end
t2=clock;
if ii<=3
cc=etime(t2,t1);
disp(['大约需要计算',num2str(length_txy*cc/3600),'小时'])
end
end
figure
scatter3(PhaseSto(:,1),PhaseSto(:,2),PhaseSto(:,3),50,'bo','filled')
xlabel('tx')
ylabel('ty')
title('Qxy相图')
end
function [op]=FinalSize_Hami(t,tx,ty)
global Nx Ny
%Nx=1;%x向原胞数
%Ny=2;%y向原胞数
H0=zeros(4,4);
H0(1,3)=tx;
H0(1,4)=ty;
H0(2,3)=-ty;
H0(2,4)=tx;
H0(3,1)=tx;
H0(3,2)=-ty;
H0(4,1)=ty;
H0(4,2)=tx;
H1=zeros(4,4);
H1(1,3)=t;
H1(4,2)=t;
H1T=H1.';%纯转置
H2=zeros(4,4);
H2(1,4)=-t;
H2(3,2)=-t;
H2T=H2.';%纯转置
vec_len=Nx*Ny;
HH0=kron(diag(ones(1,vec_len)),H0);
one_sto=[];
for ii=1:vec_len-1
if ii/Nx==fix(ii/Nx)%整数
one_sto=[one_sto,0];
else
one_sto=[one_sto,1];
end
end
HH1=kron(diag(one_sto,1),H1)+kron(diag(one_sto,-1),H1T);
HH2=kron(diag(ones(1,vec_len-Nx),-Nx),H2)+...
kron(diag(ones(1,vec_len-Nx),Nx),H2T);
op=HH0+HH1+HH2;%总的哈密顿量
end
function [op]=ProductFourPoint(center,len)
%输入中心center坐标[x,y]和一个原胞中四个原子的相邻两两距离len(晶格常数的倍数)
%输出的是[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意我认为:
% 3————1
% | |
% | |
% 2————4
%
xc=center(1);
yc=center(2);
L=0.5*len;
x1=xc+L;y1=yc+L;
x2=xc-L;y2=yc-L;
x3=xc-L;y3=yc+L;
x4=xc+L;y4=yc-L;
op=[x1,y1;...
x2,y2;...
x3,y3;...
x4,y4];
end
function [opp]=FourIndex(c_index,incellX,incellY)%输入原胞索引和胞内胞间边长,输出一个原胞内四个原子的坐标
global d
%原胞索引形式为:[a,b]
%注意输出形式为:
%[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意坐标原点(0,0)是u11所处原胞的3号原子
aa=c_index(1);
bb=c_index(2);
x3=(bb-1)*d;
y3=-(aa-1)*d;
x1=x3+incellX;
y1=y3;
x2=x3;
y2=y3-incellY;
x4=x1;
y4=y2;
opp=[x1,y1;x2,y2;x3,y3;x4,y4];
end
体四极矩参考的公式:

ref就是文章开头的那个ref。
可能电偶极矩就是极化数

也分为体电偶极矩(体极化数,表征边界态,威尔逊环)和边电偶极矩(边极化数,表征角态,嵌套威尔逊环),然后根据边电偶极矩可以算出体四极矩。
威尔逊环也可以在半开放边界下构建
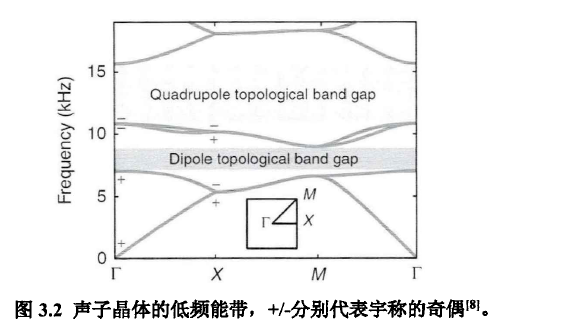

REF:

该模型满足C2旋转对称性,所以导致体电偶极矩量子化为0
clear;clc
syms t tx ty kx ky
H0=sym(zeros(2,2));
H0(1,1)=tx+t*exp(1j*kx);
H0(1,2)=ty+t*exp(1j*ky);
H0(2,1)=-ty-t*exp(-1j*ky);
H0(2,2)=tx+t*exp(-1j*kx);
H1=sym(zeros(2,2));
H1(1,1)=tx+t*exp(-1j*kx);
H1(1,2)=-ty-t*exp(1j*ky);
H1(2,1)=ty+t*exp(-1j*ky);
H1(2,2)=tx+t*exp(1j*kx);
Hami=[sym(zeros(2,2)),H0;H1,sym(zeros(2,2))];
Hami2=subs(Hami,{kx,ky},{-kx,-ky});
s0=eye(2);
sx=[0,1;1,0];
sy=[0,-1*1i;1i,0];
sz=[1,0;0,-1];
tau0=sym(eye(2));
C2=-1j.*kron(tau0,sy);
C2*Hami*inv(C2)-Hami2
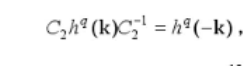

算体偶极矩Px Py(实空间法,不清楚是否正确)的代码(由于C2对称性导致量子化为0)
似乎是要一边开边界一边周期边界来算体偶极矩?
function []=RealSpaceQxy_2DSSH()
clear;clc;
global Nx Ny d t
Nx=20;%x向原胞数,一个原胞四个原子
Ny=20;%y向原胞数,一个原胞四个原子
d=1;%晶格常数
t=1;
tx=0.5;
ty=0.5;
len=0.5*d;
a1=[d,0];%正空间基矢
a2=[0,-d];%倒空间基矢
para0=0;%为0开启能带图绘制和开启Qxy的计算
para=0;%为0开启波函数绘制
para2=0;%为0开启画相图
%mode_index=2;%按照特征值实部从小到大的索引
if para0==0
delete('sort_vec.mat');
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[sortRe_val,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
save('sort_vec.mat','sort_vec');
figure(1)
plot(1:length(sortRe_val),sortRe_val,'b.','MarkerSize',10)
xlabel('mode-number')
ylabel('Re-eigenVal')
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para0==0
intercellX=d/(abs(tx/t)+1);%原胞之间边长的距离,x向
incellX=d-intercellX;%原胞内边长的距离,x向
intercellY=d/(abs(ty)/abs(t)+1);%原胞之间边长的距离,y向
incellY=d-intercellY;%原胞内边长的距离,y向
Lx=(Nx-1)*d+incellX;%有限结构x向边长
Ly=(Ny-1)*d+incellY;%有限结构x向边长
Cell_index=[];%原胞索引(一个原胞四个原子)
for uu=1:Ny
for vv=1:Nx
Cell_index=[Cell_index;uu,vv];
end
end
num2=[4:4:Nx*Ny*4];%序号
num1=num2-3;
StoSite=zeros(Nx*Ny*4,2);%第一二列是xy实际坐标,和列波函数的顺序是完全对应的
for zz=1:length(Cell_index)
n1=num1(zz);
n2=num2(zz);
Site4=FourIndex(Cell_index(zz,1:2),incellX,incellY);
StoSite(n1:n2,1:2)=[Site4];
end
xy=StoSite(:,1).*StoSite(:,2);%xy算符结果,列向量
xy=exp(xy./(Lx*Ly).*(2*pi*1j));%列向量
Q=diag(xy);
lie=size(sort_vec,2);
U=sort_vec(:,1:lie/2);%选择Re(E)<0的波函数,选择一半,选择gap下的所有波函数
%U=sort_vec(:,lie/2+1:end);%一个怪异的选择
S=U'*Q*U;
Qxy=angle(det(S)*sqrt(det(Q')))/(2*pi);
disp(['Real_Space_Qxy=',num2str(Qxy)]);
%由于这个模型只有一个gap,所以算实空间体极化数的波函数选择和Qxy是完全一样的
%下面是实空间算法算体偶极矩(也就是体极化数)
X=StoSite(:,1);
Y=StoSite(:,2);
X=exp(X./(Lx).*(2*pi*1j));%列向量
Y=exp(Y./(Ly).*(2*pi*1j));%列向量
QX=diag(X);
QY=diag(Y);
SX=U'*QX*U;
SY=U'*QY*U;
bulk_Px=angle(det(SX))/(2*pi);
bulk_Py=angle(det(SY))/(2*pi);
disp(['bulk_Px=',num2str(bulk_Px)]);
disp(['bulk_Py=',num2str(bulk_Py)]);
end
if para==0
sort_vec=cell2mat(struct2cell(load('sort_vec.mat')));%加载要处理的数据
mode_index=input('请输入模式索引:');
choice_wave=sort_vec(:,mode_index);%列向量
choice_wave=choice_wave./max(abs(real(choice_wave)));%归一化
num_sto=[4:4:length(choice_wave)];%序号
STO=[];
for ii=1:Ny
for jj=1:Nx
center=ii*a2+jj*a1;
h_index=(ii-1)*Nx+jj;
num2=num_sto(h_index);
num1=num2-3;
op=ProductFourPoint(center,len);
v0=choice_wave(num1:num2);
STO=[STO;op,v0];
end
end
figure(2)
scatter3(STO(:,1),STO(:,2),zeros(length(choice_wave),1),70,'ro','filled')
hold on
scatter3(STO(:,1),STO(:,2),real(STO(:,3)),70,'ko')
hold off
title(['t=',num2str(t),' tx=',num2str(tx),' ty=',num2str(ty),...
' mode-index=',num2str(mode_index),' Nx=',num2str(Nx),' Ny=',num2str(Ny)])
end
if para2==0
PhaseDraw();
end
end%似乎只能表征角态
function []=PhaseDraw()
global Nx Ny d t
delta=0.05;
tx0=-1.5:delta:1.5;
ty0=tx0;
length_txy=length(tx0);
PhaseSto=zeros(length_txy^2,3);%一二列tx ty值,第三列Qxy值
PhaseSto2=PhaseSto;
PhaseSto3=PhaseSto;
count=0;
for ii=1:length_txy
mark=ii/length_txy
t1=clock;
for jj=1:length_txy
count=count+1;
tx=tx0(ii);
ty=ty0(jj);
H=FinalSize_Hami(t,tx,ty);
[vec,val]=eig(H);%val是纯实的
[~,index]=sort(real(diag(val)));
sort_vec=vec(:,index);%按照特征值的实部从小到大排列对应波函数
intercellX=d/(abs(tx/t)+1);%原胞之间边长的距离,x向
incellX=d-intercellX;%原胞内边长的距离,x向
intercellY=d/(abs(ty)/abs(t)+1);%原胞之间边长的距离,y向
incellY=d-intercellY;%原胞内边长的距离,y向
Lx=(Nx-1)*d+incellX;%有限结构x向边长
Ly=(Ny-1)*d+incellY;%有限结构x向边长
Cell_index=[];%原胞索引(一个原胞四个原子)
for uu=1:Ny
for vv=1:Nx
Cell_index=[Cell_index;uu,vv];
end
end
num2=[4:4:Nx*Ny*4];%序号
num1=num2-3;
StoSite=zeros(Nx*Ny*4,2);%第一二列是xy实际坐标,和列波函数的顺序是完全对应的
for zz=1:length(Cell_index)
n1=num1(zz);
n2=num2(zz);
Site4=FourIndex(Cell_index(zz,1:2),incellX,incellY);
StoSite(n1:n2,1:2)=[Site4];
end
xy=StoSite(:,1).*StoSite(:,2);%xy算符结果,列向量
xy=exp(xy./(Lx*Ly).*(2*pi*1j));%列向量
Q=diag(xy);
lie=size(sort_vec,2);
U=sort_vec(:,1:lie/2);%选择Re(E)<0的波函数,选择一半
%U=sort_vec(:,lie/2+1:end);%一个怪异的选择
S=U'*Q*U;
Qxy=angle(det(S)*sqrt(det(Q')))/(2*pi);
%由于这个模型只有一个gap,所以算实空间体极化数的波函数选择和Qxy是完全一样的
%下面是实空间算法算体偶极矩(也就是体极化数)
X=StoSite(:,1);
Y=StoSite(:,2);
X=exp(X./(Lx).*(2*pi*1j));%列向量
Y=exp(Y./(Ly).*(2*pi*1j));%列向量
QX=diag(X);
QY=diag(Y);
SX=U'*QX*U;
SY=U'*QY*U;
bulk_Px=angle(det(SX))/(2*pi);
bulk_Py=angle(det(SY))/(2*pi);
PhaseSto(count,1:3)=[tx,ty,Qxy];
PhaseSto2(count,1:3)=[tx,ty,bulk_Px];
PhaseSto3(count,1:3)=[tx,ty,bulk_Py];
end
t2=clock;
if ii<=3
cc=etime(t2,t1);
disp(['大约需要计算',num2str(length_txy*cc/3600),'小时'])
end
end
figure
scatter3(PhaseSto(:,1),PhaseSto(:,2),PhaseSto(:,3),50,'bo','filled')
xlabel('tx')
ylabel('ty')
title('Qxy相图')
figure
scatter3(PhaseSto2(:,1),PhaseSto2(:,2),PhaseSto2(:,3),50,'bo','filled')
xlabel('tx')
ylabel('ty')
title('Px相图')
figure
scatter3(PhaseSto3(:,1),PhaseSto3(:,2),PhaseSto3(:,3),50,'bo','filled')
xlabel('tx')
ylabel('ty')
title('Py相图')
end
function [op]=FinalSize_Hami(t,tx,ty)
global Nx Ny
%Nx=1;%x向原胞数
%Ny=2;%y向原胞数
H0=zeros(4,4);
H0(1,3)=tx;
H0(1,4)=ty;
H0(2,3)=-ty;
H0(2,4)=tx;
H0(3,1)=tx;
H0(3,2)=-ty;
H0(4,1)=ty;
H0(4,2)=tx;
H1=zeros(4,4);
H1(1,3)=t;
H1(4,2)=t;
H1T=H1.';%纯转置
H2=zeros(4,4);
H2(1,4)=-t;
H2(3,2)=-t;
H2T=H2.';%纯转置
vec_len=Nx*Ny;
HH0=kron(diag(ones(1,vec_len)),H0);
one_sto=[];
for ii=1:vec_len-1
if ii/Nx==fix(ii/Nx)%整数
one_sto=[one_sto,0];
else
one_sto=[one_sto,1];
end
end
HH1=kron(diag(one_sto,1),H1)+kron(diag(one_sto,-1),H1T);
HH2=kron(diag(ones(1,vec_len-Nx),-Nx),H2)+...
kron(diag(ones(1,vec_len-Nx),Nx),H2T);
op=HH0+HH1+HH2;%总的哈密顿量
end
function [op]=ProductFourPoint(center,len)
%输入中心center坐标[x,y]和一个原胞中四个原子的相邻两两距离len(晶格常数的倍数)
%输出的是[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意我认为:
% 3————1
% | |
% | |
% 2————4
%
xc=center(1);
yc=center(2);
L=0.5*len;
x1=xc+L;y1=yc+L;
x2=xc-L;y2=yc-L;
x3=xc-L;y3=yc+L;
x4=xc+L;y4=yc-L;
op=[x1,y1;...
x2,y2;...
x3,y3;...
x4,y4];
end
function [opp]=FourIndex(c_index,incellX,incellY)%输入原胞索引和胞内胞间边长,输出一个原胞内四个原子的坐标
global d
%原胞索引形式为:[a,b]
%注意输出形式为:
%[x1,y1;x2,y2;x3,y3;x4,y4]这样的顺序
%注意坐标原点(0,0)是u11所处原胞的3号原子
aa=c_index(1);
bb=c_index(2);
x3=(bb-1)*d;
y3=-(aa-1)*d;
x1=x3+incellX;
y1=y3;
x2=x3;
y2=y3-incellY;
x4=x1;
y4=y2;
opp=[x1,y1;x2,y2;x3,y3;x4,y4];
end
算Qxy时会用到的坐标系参考
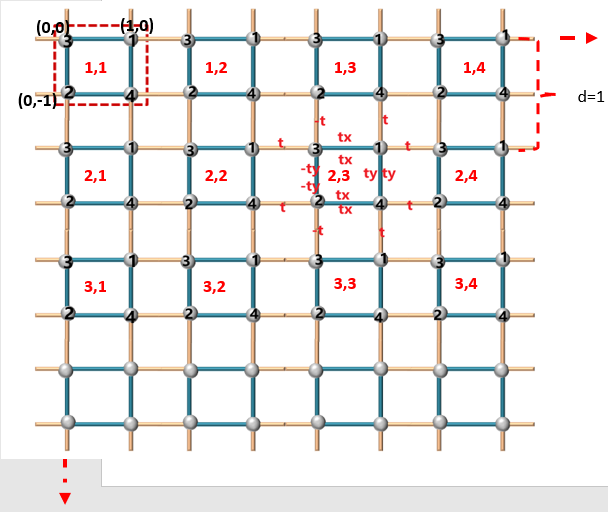
同时该模型具有时间反演对称性:TH∗(k)T−1=H(−k)\Large \mathcal{T}H^{*}(k)\mathcal{T^{-1}}=H(-k)TH∗(k)T−1=H(−k),其中T=I^4×4\Large \mathcal{T}=\mathbf{\hat{I}}_{4\times4}T=I^4×4(注意单位矩阵大小视哈密顿量矩阵大小而定)
如果tx=ty,该模型具有C4对称性(如下C4对称性)
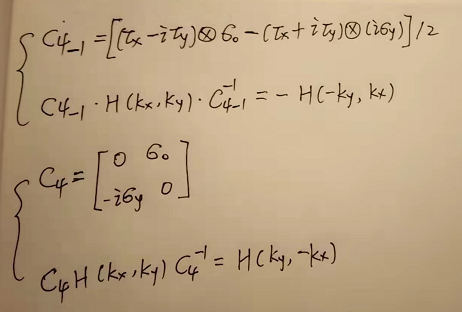

该模型具有粒子空穴对称性
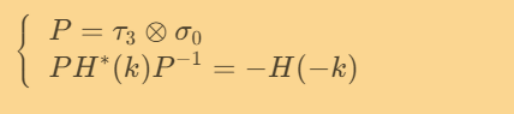
标准BBH模型
syms lam gam kx ky
s0=eye(2);
sx=[0,1;1,0];
sy=[0,-1*1i;1i,0];
sz=[1,0;0,-1];
T4=kron(sx,s0);
T3=kron(sy,sz);
T2=kron(sy,sy);
T1=kron(sy,sx);
S=kron(sz,s0);
H_BBH=(gam+lam*cos(kx)).*T4-lam*sin(kx).*T3-(gam+lam*cos(ky)).*T2-lam*sin(ky).*T1;
标准BBH模型具有如下所示的粒子空穴对称性
{P=τ3⊗σ0PH∗(k)P−1=−H(−k)\Large \left\{\begin{array}{l} P=\tau_{3} \otimes \sigma_{0} \\ P H^{*}(k) P^{-1}=-H(-k) \end{array}\right.⎩⎨⎧P=τ3⊗σ0PH∗(k)P−1=−H(−k)







 文章通过MATLAB代码展示了如何计算二维材料的体四极矩和角态四极矩,具体涉及哈密顿量的构建、能带图的绘制以及波函数的分布。此外,讨论了模型的C2旋转对称性和时间反演对称性,以及粒子空穴对称性。在不同边界条件下,分析了体偶极矩(体极化数)的量子化特性。
文章通过MATLAB代码展示了如何计算二维材料的体四极矩和角态四极矩,具体涉及哈密顿量的构建、能带图的绘制以及波函数的分布。此外,讨论了模型的C2旋转对称性和时间反演对称性,以及粒子空穴对称性。在不同边界条件下,分析了体偶极矩(体极化数)的量子化特性。
















 2988
2988

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








