机器视觉——相机标定（摄像机标定）

1 摄像机标定

• 摄像机标定目的：建立世界坐标中三维点与像素坐标系中二维点的相关关系。
• 针孔模型：摄像机的线性模型是在理想情况下的成像模型，即光学中的中心投影，我们通常也称为针孔模型。

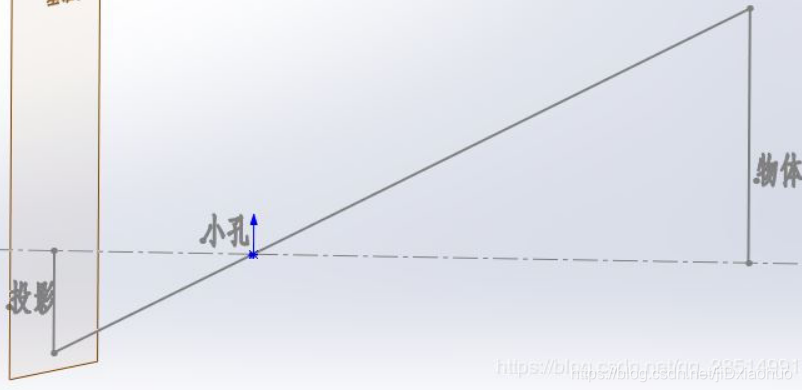
如果按照实际的投影关系建立坐标系，那么投影坐标和物体坐标的符号总是相反的，考虑起来不太方便，于是在“数学上”把投影平面平移到其关于小孔对称的位置，这样投影坐标和物体坐标符号就相同了，示意图如下:

1.1 四大坐标系

在视觉测量中，需要进行的一个重要预备工作是定义四个坐标系的意义，即世界坐标系、摄像机坐标系 、 图像坐标系、 像素坐标系 。

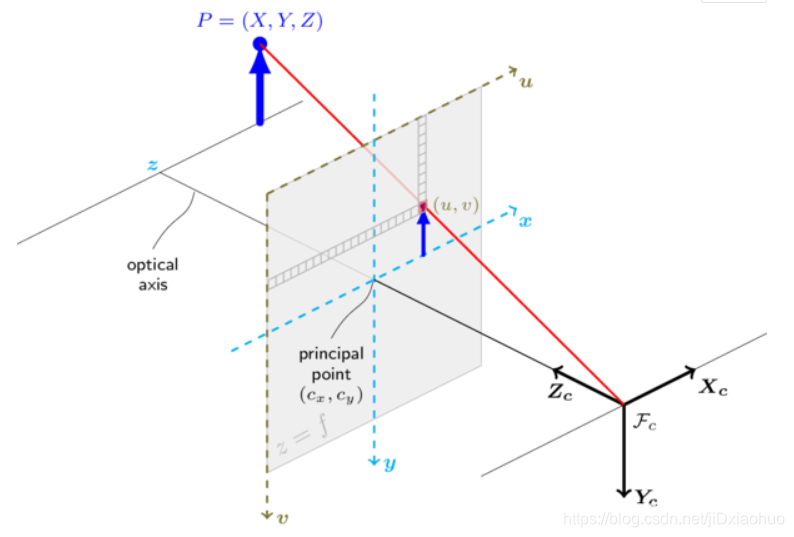
• {world}，{camera}，{picture}和{pixel}坐标系的坐标用下标来区分，分别是W，c，p，pix
• {world}，{camera}，{picture}坐标系单位为长度，一般为mm；{pixel}坐标系单位为像素，一般为pix
• {world}坐标系为世界坐标系，可以任意指定，其他坐标系都有明确的定义
• {camera}坐标系为摄像机坐标系，原点在小孔的位置，z轴与光轴重合，Xc轴和Yc轴分别和投影面两边平行
• {picture}坐标系为图像坐标系，光轴和投影面的交点为原点，Xp轴和Yp轴分别和投影面两边平行
• {pixel}坐标系为像素坐标系，从小孔向投影面方向看，投影面的左上角为原点Opix，uv轴和投影面两边重合

1.2 坐标系转换

1.2.1 {world}到{camera}

设某点在{world}坐标系中的坐标为
，
该点在{camera}坐标系中的坐标为
，
则有

其中R是正交旋转矩阵：

Rx Ry Rz 分别为矩阵沿着对应轴的旋转矩阵
具体推导公式列出一个 其他同理

T是平移矩阵：

为各个方向上的位移偏移量

确定R需要3个参数，确定T需要3个参数，共需6个参数，这6个参数称为摄像机的外部参数。（在单目相机中外参没有多少意义。只有在双目相机中，以另一个摄像头为坐标系，得出的相对另一个摄像头的旋转和平移矩阵才有实际意义）

1.2.2 {camera}到{picture}

设空间点$X_c$在{camera}下： P c = [ x c , y c , z c , 1 ] T P_{c}=\left [ x_{c},y_{c},z_{c},1 \right ]^{T}