Information Sparsification in Visual-Inertial Odometry论文理解

前言

网上关于先验信息矩阵稀疏化的中文资料非常少，而个人觉得NFR(Nonlinear Factor Recovery)在提高边缘化后的信息矩阵稀疏性，提升非线性求解效率和精度方面具有重要作用。与本文相关的文章有Nonlinear factor recovery for long-term SLAM和Visual-Inertial Mapping with Non-Linear Factor Recovery。前者首次提出并证明了NRF，后者将其应用于整个VI SLAM系统，得到了很好的效果。本文所介绍的文章，是将Information Sparsification应用到local BA中，对边缘化后的信息矩阵进行稀疏化。

摘要

本文的出发点就是，在现在的基于优化的VIO中，为了限制计算复杂度，对变量进行边缘化，但是产生了一个稠密的先验因子图，显著的降低了精度和效率。(这里为什么稠密性会降低状态估计的精度，还没有想清楚)当前的先进的方法，通选择性地丢弃观测以及边缘化额外的变量来解决这个问题。但是，这种策略从信息理论的角度来说是次优的。针对该问题，本文执行稠密的边缘化步骤，然后保留其中的信息。我们的方法是使用非线性因子图通过最小化信息损失对稠密的先验信息矩阵进行稀疏化，所得到的因子图保留了信息的稀疏性，结构相似性，以及非线性。为了验证本文的方法，在实际数据上进行了对比实验，实验结果证明了本文方法能够达到可与现有方法媲美的程度。

引言

However, there are
several known drawbacks in a fixed-lag framework. 1) In order to bound computational complexity, a fixed-lag smoother marginalizes out variables, which requires linearizing the system by fixing linearization points. As a consequence, it no longer describes the original nonlinear optimization. 2) This in turn limits the ability of the fixed-lag smoother
to converge to the optimal solution at future timesteps because marginalized variables are no longer optimizable. 3) Furthermore, repeating the marginalization process creates a prior that densely connects the remaining variables, which significantly decreases computational efficiency.
上述三点是目前基于优化的方法中普遍存在的问题，这也是目前一部分前沿的工作是从这几个角度对优化框架进行改进。

Problem Formulation

本节主要介绍了一些在优化方法中通用的变量表达与优化求解方法。
窗口内包含的帧为$m$个连续的关键帧，$n$个最近的帧，$p$个环境特征。
优化对象也是IMU状态与偏置
$$x_i=[{\xi }_i^T,{\mathbf{v}}_i^T,{\mathbf{b}}_i^T{]}^T$$
每个环境特征$L_j$世界坐标系下的三维点来表示。
接下来就是包含了先验残差，IMU预积分残差和重投影残差的总的残差方程。

Fixed-Lag VIO with Sparaification

边缘化是通过舒尔补过程实现的，对于当前窗口中的变量，其对应的信息矩阵${\Lambda }_{(MB)}$为
$${\Lambda }_{(MB)}=H_0^T{\Sigma }_0^{-1}{H}_0+H_{I_i}^T{\Sigma }_{I_i}^{-1}{H}_{I_i}+{\Sigma }_{c_{ij}\in {\mathbb{C}}_i}{H}_{c_{ij}}^T{\Sigma }_{c_{ij}}^{-1}{H}_{c_{ij}}$$
注意到${\Lambda }_{(MB)}$是稀疏的，并且其中的元素对应图的连接性。定义${\chi }_R\in {\chi }_{(MB)}$为边缘化后余下的变量，${\chi }_M\in {\chi }_{(MB)}$为需要被边缘化的变量，我们执行舒尔补过程
$$\begin{gathered} {\Lambda }_{(MB)}=\left[\begin{array}{cc}{\Lambda }_{{\chi }_R{\chi }_R}& {\Lambda }_{{\chi }_M{\chi }_R}\\ {\Lambda }_{{\chi }_R{\chi }_M}& {\Lambda }_{{\chi }_M{\chi }_M}\end{array}\right] \\ {\Lambda }_t={\Lambda }_{{\chi }_R{\chi }_R}-{\Lambda }_{{\chi }_R{\chi }_M}{\Lambda }_{{\chi }_M{\chi }_M}^{-1}{\Lambda }_{{\chi }_M{\chi }_R} \end{gathered}$$
其中${\Lambda }_t$是对应于稠密先验的信息矩阵，由于边缘化过程降低了因子图的稀疏性，其降低了算法效率。针对该问题，目前基于关键帧的方法如OKVIS何VINS-MONO选择性的丢弃一些观测，保持边缘化中的稀疏性。对于没有被最近的帧观测到的环境特征，也被一起边缘化。需要注意到，这种边缘化策略虽然保证了效率，但是潜在地损失了对这些被边缘化的环境特征迭代估计器状态的能力，因此降低了精度。这也是本文的动机所在。

A. 边缘化策略
本文的方法保持了$n$个最近的帧和$m$个关键帧，当一个新的帧$F_i$进入到窗口中，我们检查$F_{i-n}$是否为关键帧，根据此选择中间帧边缘化和关键帧边缘化策略。为了保证一致性，我们使用FEJ策略。
1）Midframe Marginalization: 丢弃中间帧的所有的重投影误差，不仅保证稀疏性，还能避免对地标的重复观测，当机器人在静止的时候。仅保留惯性约束。
2）Keyframe Marginalization：如果$F_{i-n}$是关键帧，我们对最老的关键帧和仅与该关键帧相连的环境特征进行边缘化。与已有的方法不同，余下的特征在边缘化步骤中被保留，在后续的非线性优化中继续优化。但是所产生的${\Lambda }_t$仍然可能非常大，本文接下来介绍一种稀疏化的方法。

B. 信息稀疏化
这里先介绍一下思想：信息矩阵就是对应因子图的联合概率分布的协方差的逆，这里要和残差的协方差矩阵区分开来。信息矩阵越稠密，对应的因子图中的连接就越稠密，而稀疏化的目标是，通过近似操作，找到稠密因子图对应的稀疏形式，使得边缘化后被边缘的约束只对相连接的节点有约束，而不对节点之间产生新的约束。即构造一种近似等价的因子图，残差对应边对应于所构造的观测。

下面进行具体的论文内容的介绍：
稠密信息矩阵${\Lambda }_t$定义了一个多变量的高斯模型$p({\chi }_t)\sim \mathrm{N}({\mu }_t,{\Lambda }_t)$,其中${\mu }_t$等于当前的线性化点${\chi }_t$。本文使用全局的线性化点。
我们的方法首先求解一个因子图模型$\Gamma$，其对应着一个稀疏的分布$p_s({\chi }_t)\sim \mathrm{N}({\mu }_s,{\Lambda }_s)$。我们采用NFR[30]对近似的分布进行求解，通过最小化$p_s({\chi }_t),p({\chi }_t)$之间的KLD散度：
$$D_{KL}(p({\chi }_t)||p_s({\chi }_t))=\frac{1}{2}(<{\Lambda }_s,{\Sigma }_t>-logdet({\Lambda }_s)+\Vert {\Lambda }_s^{\frac{1}{2}}({\mu }_s-{\mu }_t){\Vert }_2^2-d)$$
其中，${\Sigma }_t={\Lambda }_t^{-1}$，左边第一项为矩阵的内积。
对于$\Gamma$中的每个因子，必须定义其对应的观测，以及观测模型，以及观测的协方差${\Sigma }_s={\Lambda }_s^{-1}$，有$z_s=h_s({\mu }_s)+v,v\sim \nu (0,{\Sigma }_s)$.首先，我们定义$z_s=h_s({\mu }_t)$,这会得出${\mu }_s={\mu }_t$的近似假设。对于每个观测，对${\Lambda }_r$的恢复在Section IV-C中介绍。

为了设计这个拓扑，我们需要考虑(1) ${\Lambda }_s$应该尽可能的近似${\Lambda }_t$, (2) $\Gamma$具有稀疏性，(3) $\Gamma$和原始的拓扑图具有结构相似性。在原始的信息矩阵中${\Lambda }_t$中的只要元素都位于主对角线上，非对角线上的元素对应IMU状态和环境特征。因此，我们设计了如Fig.3c的拓扑结构，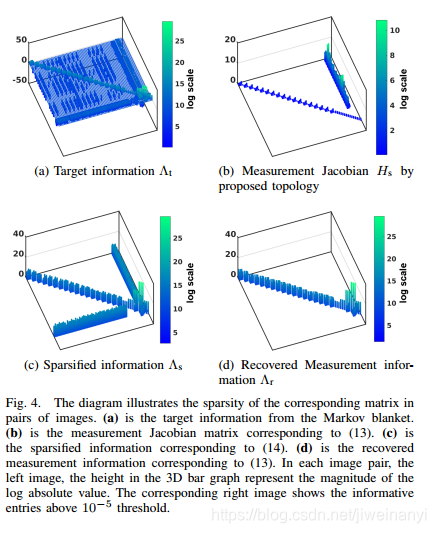
这个结构还是挺明晰的，其基本思想是新增加的节点之间的约束本质上是对节点自身的约束，所构造了拓扑结构只保留了最基本的节点的约束和节点之间的约束，因此是最稀疏的一种结构，所有的稠密的稀疏矩阵都可以对应到这种稀疏的结构。
稠密的先验信息总是包含了关键帧$K_{k-m+1}$对应的IMU状态$x_R$和所有的环境特征$L_R={\mathbf{l}}_p\in {\chi }_t$
令$R_R$表示旋转，$p_R$表示平移，其对应的位姿表示为${\xi }_R$，我们设计了两种非线性拓扑观测模型以将${\Lambda }_t$中最主要的信息元素包含进来。首先，对于独立的先验知识在IMU状态$x_R$上，有
$h_r({\xi }_R)={\xi }_R,h_r({\mathbf{v}}_R)={\mathbf{v}}_R,h_r({\mathbf{b}}_R)={\mathbf{b}}_R$
第二种就是相对的位姿和环境特征之间的观测模型
$$h_r({\xi }_R,{\mathbf{l}}_R)=R_R^{-1}({\mathbf{l}}_p-{\mathbf{p}}_R),{\mathbf{l}}_p\in {\chi }_t$$
为了基于上述观测方程构建这个稀疏的信息矩阵${\Lambda }_s$，我们定义了如下的矩阵
$$\begin{gathered} H_s=\left[\begin{array}{c}⋮\\ H_s^{(j)}\\ ⋮\end{array}\right]; \\ {\Lambda }_r=\left[\begin{array}{ccc}\ddots & 0& 0\\ 0& {\Lambda }_r^{(j)}& 0\\ 0& 0& \ddots \end{array}\right] \end{gathered}$$
其中，$H_s^{(j)}$是第$j$个非线性拓扑观测模型的雅克比矩阵，${\Lambda }_r^{(j)}$是未知的信息矩阵，这里其实是对应的该节点本身的不确定性。一个$H_s$的示例如图Fig.4b，然后${\Lambda }_s$能够被表示为
$${\Lambda }_s=H_s^T{\Lambda }_r{H}_s$$
接下来对独立的非线性拓扑观测信息矩阵${\Lambda }_r$进行求解。

C. 恢复出拓扑观测协方差
由于已知${\Lambda }_t,H_s$,我们能够构造一个基于KLD散度的凸优化方程对${\Lambda }_r$进行求解：
$$min{C}_{KL}=<H_s^T{\Lambda }_r{H}_s,{\Sigma }_t>-logdet(H_s^T{\Lambda }_r{H}_s),s.t.{\Lambda }_r>=0$$
由于本文设定的观测模型总是正定的可逆的，所以我们可以给出如下的解：
$${\Lambda }_r^{(i)}=({H_s{\Sigma }_t{H}_s^T}^{(i)}{)}^{-1}$$
该解释独一无二的，并且是最优的。
Fig.4d给出了所恢复出来的稀疏信息矩阵${\Lambda }_r$的示例，每个块对应一个非线性拓扑观测。然后，本文的方法将原始的信息矩阵${\Lambda }_t$替换为所构造的稀疏的拓扑图$varGamma$。在总的残差方程中，加入稀疏后的观测残差以及其对应的协方差${\Sigma }_r^{(i)}={{\Lambda }_r^{(i)}}^{-1}$

实验结果

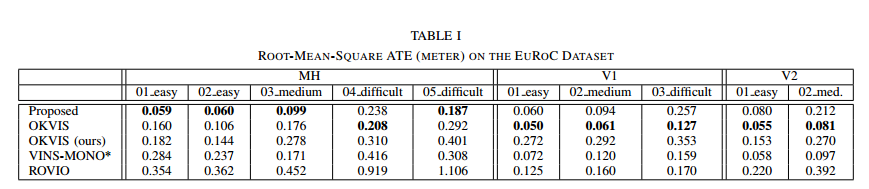
本文的结果优于不加闭环的VINS-MONO的结果。