从投影的角度理解 SVD 分解

前言

SVD分解是一种特别有意思的降维手段，它在降维的同时还可以发现某些潜在的隐向量，这些向量对于数据之间的潜在关系有很大的帮助。
下面我们使用一个例子来逐步导出SVD的近似分解，理解如何通过SVD来发现数据之间的潜在关系。

数据集

假设我们手上有一个电影评分矩阵$A$,$A_{i,j}$ 表示第$i$ 个人对第$j$ 个电影的打分（0-5，打分越高说明评价越高）。一共有6个人，5个电影。这 5部电影前三部是科幻电影，最后两部是爱情电影。

任务

我们把矩阵$A_{6\times 5}$ 看做是6个 $R^5$ 空间上的点形成的一个子空间（或者集合），现在我们想在$R^5$ 上找一个单位向量$v\in R^5$,使得这个向量穿过这个子空间里面尽量多的点，或者说让这个子空间里的点离这个向量的距离平方和最小。

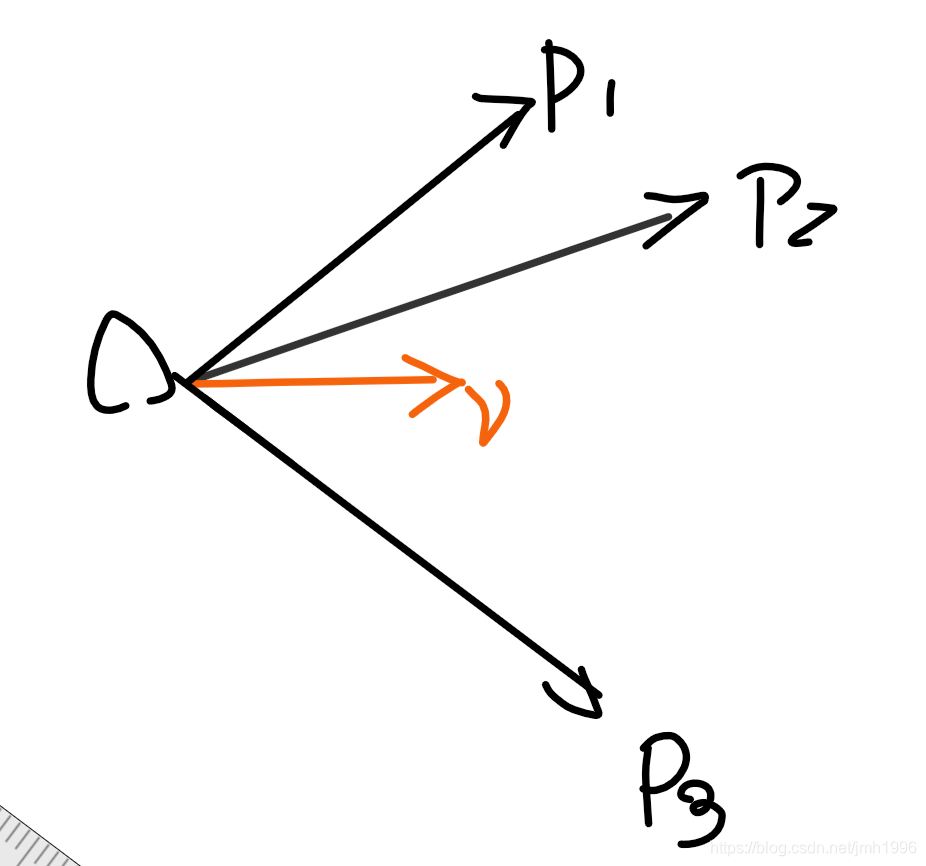
求解

就如上图所示，寻找一个$v$,使得$P_1,P_2,P_3$ 到这个$v$所在的距离和的平方最小。这个问题实际上等价于：寻找一个$v$,使得$P_1,P_2,P_3$ 在这个$v$方向的投影的值的平方和最大。为什么呢？

对于$P_2$ 来说，$\overrightarrow{OP}$模长是固定的，$|\overrightarrow{OP}{|}^2=距{离}^2+投{影}^2$，投影最大了那么距离肯定 就是最小了。
OK,我们假设要找的方向向量为$v$ ,那么$A$ 所有的行 作为$R^5$ 上的点在$v$ 上的投影为：$A_{6\times 5}{v}_{5\times 1}$ ，这是一个列向量，第$i$ 元素表示第$i$ 个点的投影值,这些投影的平方和：$(Av{)}^T(Av)$，显然这是一个随着$v$变化的函数，记为$f(v)=(Av{)}^T(Av)$，我们求这个函数在$v$是单位方向向量的条件下的最大值。
即:
$maxf(v)=(Av{)}^T(Av)$
$s.t.v^{T}v=1$

为什么要约束$v$ 是单位向量？因为只有$v$ 是单位向量的时候，$Av$的每个元素才是点在这个方向的投影值。
对于这个带约束的优化问题，我们引入拉个朗日因子，使得问题变成没有约束：
$maxh(v,\lambda )=(Av{)}^T(Av)-\lambda (v^{T}v-1)$
同时我们也会得到拉格朗日乘子的物理意义。

然后，对$h(v,\lambda )$ 求偏导，使得偏导为0，得到取得最优解的条件: $A^{T}Av=\lambda v$, 可以看出$v$ 就是矩阵$A^{T}A$ 的特征向量，而 $\lambda$ 是$A^{T}A$ 的特征值。

我们使用numpy 求出 $v$ 和 $\lambda$ 来。

>>> import numpy as np


>>> A=np.mat([[1,1,1,0,0],
		[3,3,3,0,0],
	  	[4,4,4,0,0],
	  	[5,5,5,0,0],
		[0,2,0,4,4],
		[0,0,0,5,5],
		[0,1,0,2,2]])

求$v,\lambda$:

>>> _lambda,_v=np.linalg.eig(A.T *A)

得到：$\lambda$=array([ 1.55775728e+02, 9.04137413e+01, -2.78499845e-15, 1.81053094e+00, 2.46519033e-32])。我们只取最大的两个特征值：155.775和90.413.
同样的，我们把_v里面的第0,1列保留下来，把第2,3,4列丢掉。
值得注意的是$v$ 的每一列的模都是 1 (即 $v^{T}v=1$) ！.

>>> v=_v[:,0:2] ==>取前最大特征值对应的那两列
>>> v
matrix([[ 0.56225841,  0.12664138],
        [ 0.5928599 , -0.02877058],
        [ 0.56225841,  0.12664138],
        [ 0.09013354, -0.69537622],
        [ 0.09013354, -0.69537622]])
>>> v.T * v ===>v都是单位方向向量!
matrix([[1.00000000e+00, 2.74951927e-17],
        [2.74951927e-17, 1.00000000e+00]])
>>> _lambda=_lambda[0:2] ==>取两个最大的特征值
>>> _lambda
array([155.77572778,  90.41374128])

找到的这两个方向向量说明，这6个人的评分构成的6个$R^5$ 向量 在这两个方向上的投影平方和最大。而这两个方向其实就是对应两种 潜在人格：爱好科幻电影以及爱好爱情电影。任何一个用户在这两个方向的投影，其实就是他的两种潜在人格的偏重。

而且我们还能得出：在这两个方向上的投影平方和其实就是刚刚引入的拉格朗日乘子$\lambda$。 正是因为$\lambda$ 的这种物理意义使得我们应该取最大的特征值以及对应的特征向量，因为在这些方向上 投影平方和最大，信息损失最小。

首先从理论上分析，因为投影平方和是$(Av{)}^{T}Av$, 而$(Av{)}^{T}Av=v^T(A^{T}Av)=v^T(\lambda v)=\lambda v^{T}v=\lambda$。

其次，在数值上验证：

>>> A*v    ===> A的所有行在v上的投影
matrix([[ 1.71737671,  0.22451218],
        [ 5.15213013,  0.67353654],
        [ 6.86950685,  0.89804872],
        [ 8.58688356,  1.12256089],
        [ 1.9067881 , -5.62055093],
        [ 0.90133537, -6.9537622 ],
        [ 0.95339405, -2.81027546]])
 >>> (A*v).T *(A*v)  ===>投影的平方和
matrix([[ 1.55775728e+02, -7.06352805e-16],
        [-7.06352805e-16,  9.04137413e+01]])

只看对角元的话，就是对应的 $\lambda$ ，或者说我们把v的两列分别取出来观察。
取出第一列，$A{v}_1$ 表示这6个人在第一种人格 上的投影：

>>> A*v[:,0]
matrix([[1.71737671],
        [5.15213013],
        [6.86950685],
        [8.58688356],
        [1.9067881 ],
        [0.90133537],
        [0.95339405]])

这个投影向量的模长的平方也就是${\lambda }_1$的值155.775：

>>> (A*v[:,0]).T*(A*v[:,0])
matrix([[155.77572778]])

如果我们把$A{v}_1$ 给单位化一下：$\frac{A{v}_1}{|A{v}_1|}$ 或者$\frac{A{v}_1}{\sqrt{{\lambda }_1}}$ 得到：

>>> A*v[:,0]/np.sqrt(_lambda[0])
matrix([[0.13759913],
        [0.41279738],
        [0.5503965 ],
        [0.68799563],
        [0.15277509],
        [0.07221651],
        [0.07638754]])

这玩意就是SVD里面 $U$表这些6个用户的第一人格投影得到的特征向量。
同样，我们取出$v$的第二列来：
$A{v}_2$ 表示 这六个用户在第二种人格上的投影：

>>> A*v[:,1]
matrix([[ 0.22451218],
        [ 0.67353654],
        [ 0.89804872],
        [ 1.12256089],
        [-5.62055093],
        [-6.9537622 ],
        [-2.81027546]])

同样它的模长的平方也是对应的${\lambda }_2$的值 90.413

>>> (A*v[:,1]).T *A*v[:,1]
matrix([[90.41374128]])

然后把$A{v}_2$ 单位化：$\frac{A{v}_2}{|A{v}_2|}$或者 $\frac{A{v}_2}{\sqrt{{\lambda }_2}}$得到

>>> A*v[:,1]/np.sqrt(_lambda[1])
matrix([[ 0.02361145],
        [ 0.07083435],
        [ 0.09444581],
        [ 0.11805726],
        [-0.59110096],
        [-0.73131186],
        [-0.29555048]])

这玩意就是SVD里面 $U$表这些6个用户的第二人格投影得到的特征向量。
把这两列人格投影堆在一起，于是得到$U$:

>>> U
matrix([[ 0.137,  0.023],
        [ 0.412,  0.07 ],
        [ 0.55 ,  0.094],
        [ 0.687,  0.118],
        [ 0.152, -0.591],
        [ 0.072, -0.731],
        [ 0.076, -0.295]])

然后，我们把模长也写成矩阵$\sigma$

>>> sigma
matrix([[12.48101469,  0.        ],
        [ 0.        ,  9.50861406]])

于是可以得到：$\frac{Av}{\sigma }=U$,即：$Av=U\sigma$

>>> A*v-U*sigma  ===>验证码左右两边是否相等
matrix([[ 0.0074777 ,  0.00581406],
        [ 0.00995208,  0.00793355],
        [ 0.00494877,  0.00423899],
        [ 0.01242646,  0.00054444],
        [ 0.00967387, -0.00096002],
        [ 0.00270231, -0.00296532],
        [ 0.00483693, -0.00523432]])

可以看到，$Av-U\sigma$ 的差很小。
两边再右乘一个矩阵 $v^T$,得到：
$A=U\sigma v^T$.
这个就是我们想要的SVD分解了！