smac 路径优化器分析——平滑度成本分析

参考

Apollo 离散点曲线平滑度优化

相关文章

smac 路径优化器分析——曲率成本分析

smac 路径优化器分析——距离成本和代价地图成本分析

平滑度成本函数

Smac 用向量和的模的平方来作为曲线离散点的平滑度，非常巧妙。
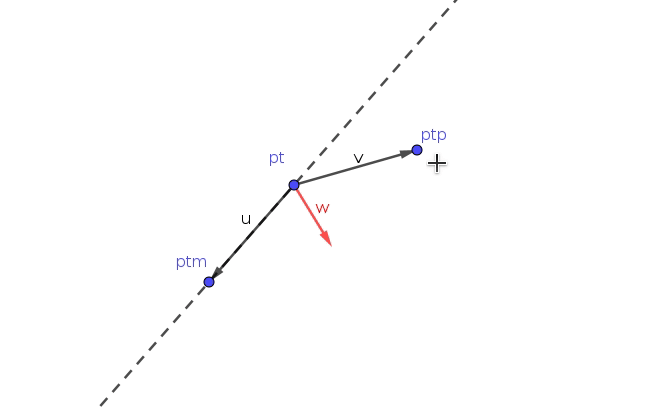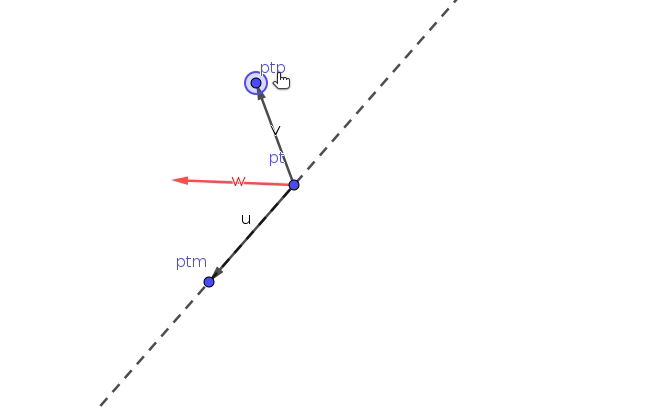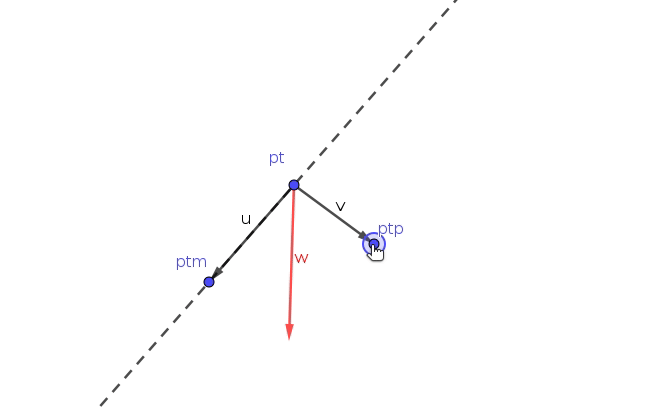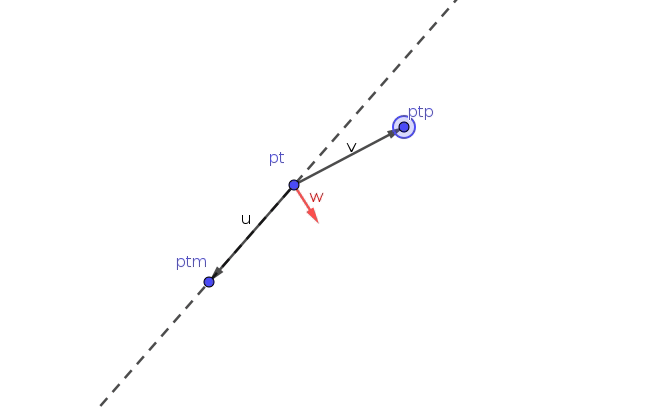
离散点顺序： pt_m -> pt -> pt_p
向量 u 是 pt -> pt_m，向量 v 是 pt -> pt_p，向量 w = u + v。

fig.1 向量 u 和 v 图示

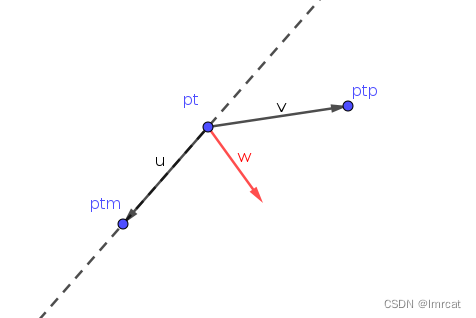
下面蓝色圆形虚线 ptmNorm 表示向量 u 的模，紫色圆形虚线 ptpNorm 表示向量 v 的模。

1. 在 u 和 v 的模大小固定情况下，夹角 α  从大到小变化（[0,π]范围），此时 w 的模是从小到大变化。

fig.2 模固定，向量夹角 176°

fig.3 模固定，向量夹角 129°

fig.4 模固定，向量夹角 27°

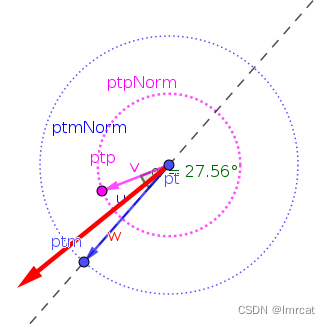
这个性质反映了向量的方向同向程度，方向越接近 w 模越大。

性质用作离散曲线点的平滑度成本函数，w 模越大反映曲线越扭曲迂回，w 模越小反映曲线越平滑前进。

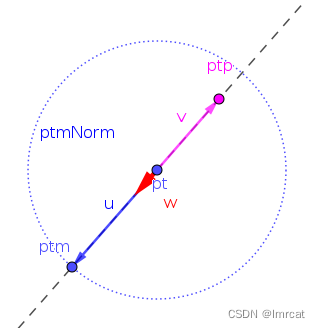
2. 在 u 和 v 的夹角固定，u 的模大小固定情况下

        a. 当 v 的模在 ptmNorm 之内，即 v 的模小于 u 的模。v 的模从小到大变化，此时 w 的模是从大到小变化。

fig.5 向量夹角固定，v 的模小于 u 的模，v 的模较小

fig.6 向量夹角固定，v 的模小于 u 的模，v 的模较大

        b. 当 v 的模在 ptmNorm 之外，即 v 的模大于 u 的模。v 的模从小到大变化，此时 w 的模是从小到大变化。

fig.7 向量夹角固定，v 的模大于 u 的模，v 的模较小

fig.8 向量夹角固定，v 的模大于 u 的模，v 的模较大

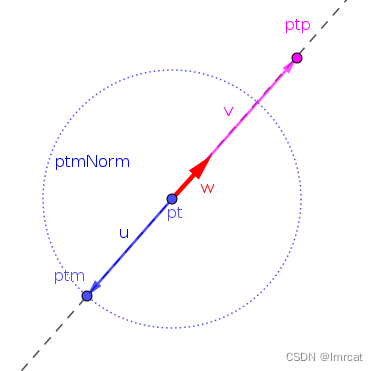
这个性质反映了向量的模差异程度，向量的模差越大，w 模越大。

该性质用作离散曲线点的平滑度成本函数，w 模越大反映离散点分布越混乱，w 模越小反映离散点分布越均匀。
任意 v 向量情况下的 w 情况如下

fig.9 任意 v 向量条件下的 w 情况

平滑度成本函数为：

 是 pt_m -> pt 向量， 是 pt_p-> pt 向量。

具体公式是

源码：

  inline void addSmoothingResidual(
    const double & weight,
    const Eigen::Vector2d & pt,
    const Eigen::Vector2d & pt_p,
    const Eigen::Vector2d & pt_m,
    double & r) const
  {
      r += weight * (
      pt_p.dot(pt_p) -
      4 * pt_p.dot(pt) +
      2 * pt_p.dot(pt_m) +
      4 * pt.dot(pt) -
      4 * pt.dot(pt_m) +
      pt_m.dot(pt_m));    // objective function value
  }

平滑度成本梯度函数

对平滑度成本函数中 pt 变量求偏导，由于求偏导将与自变量无关项视作常量，常量求导为 0，所以在这里只需要关心平滑度成本函数中与自变量 pt 相关的项即可。
提取平滑度成本函数中 pt 相关项：

矩阵表示：

源码：

  inline void addSmoothingJacobian(
    const double & weight,
    const Eigen::Vector2d & pt,
    const Eigen::Vector2d & pt_p,
    const Eigen::Vector2d & pt_m,
    double & j0,
    double & j1) const
  {
      j0 += weight *
      (-4 * pt_m[0] + 8 * pt[0] - 4 * pt_p[0]); // xi x component of partial-derivative
      j1 += weight *
      (-4 * pt_m[1] + 8 * pt[1] - 4 * pt_p[1]); // xi y component of partial-derivative
  }