smac 路径优化器分析——曲率成本分析

jucat

已于 2024-04-30 22:31:15 修改

阅读量1k

点赞数 30

分类专栏：算法文章标签：算法机器人自动驾驶

于 2024-04-17 11:50:45 首次发布

本文链接：https://blog.csdn.net/jucat/article/details/137864755

版权

算法专栏收录该内容

20 篇文章 2 订阅

订阅专栏

参考

smac 路径优化器分析——平滑度成本分析

smac 路径优化器分析——距离成本和代价地图成本分析

曲率成本函数

曲率是描述曲线局部性质的量。
一般曲率由三点求外界圆的 R 来计算，但是这里是通过曲率的定义来计算。

离散点顺序： pt_m -> pt -> pt_p

曲率定义为极小弧长内转过的角度：

$\lim_{\Delta s \to 0} k=|\frac{\Delta \theta}{\Delta s}|$

向量 u 是 pt_m -> pt，向量 v 是 pt -> pt_p，向量 u 和 v 夹角 α 。

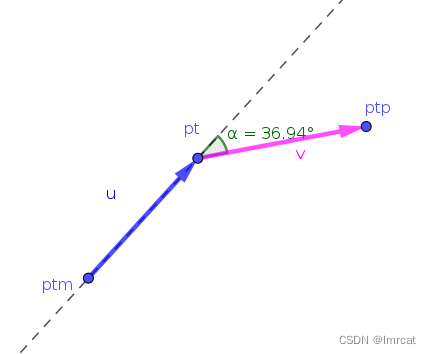
在 smac 中将向量 u 的模近似看做弧长，夹角 α 看做转角：

$k=|\frac{\Delta \alpha}{|u|}|$

这种近似计算是有条件的，先看看转角的情况：

1. 转角

以 3 个点 ptm，pt，ptp 作外接圆 c，圆心 C。β 角是弧 ptm-pt 对应的圆心角。
当向量 u 的模小于 v 的模时候，此时 β 明显小于 α 。

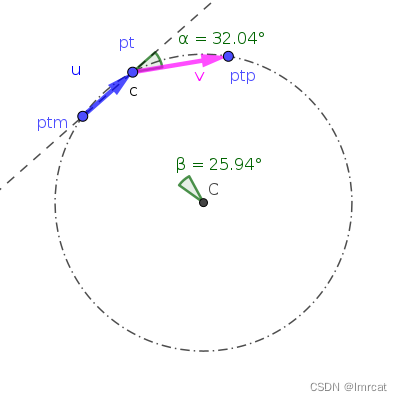
当向量 u 的模大于 v 的模时候，此时 β 明显大于 α 。

只有当 pt 落在弧 ptm 和 ptp 中间，也就是向量 u 的模等于向量 v 的模时候，才有 α = β。

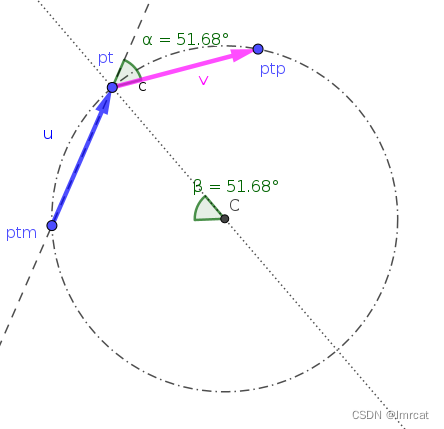
2. 弧长

假设 3 点同圆情况下，向量 u 的模相当于弧 ptm - pt 对应的弦。

弧长公式：

$L=r*\theta$

弦长公式：

$K=2*r*sin(\frac{\theta}{2})$

将两式相除，弧长 / 弦长：

$f(\theta)=\frac{r*\theta}{2*r*sin{\frac{\theta}{2}}}= \frac{\theta}{2*sin{\frac{\theta}{2}}}$

其图像如下：

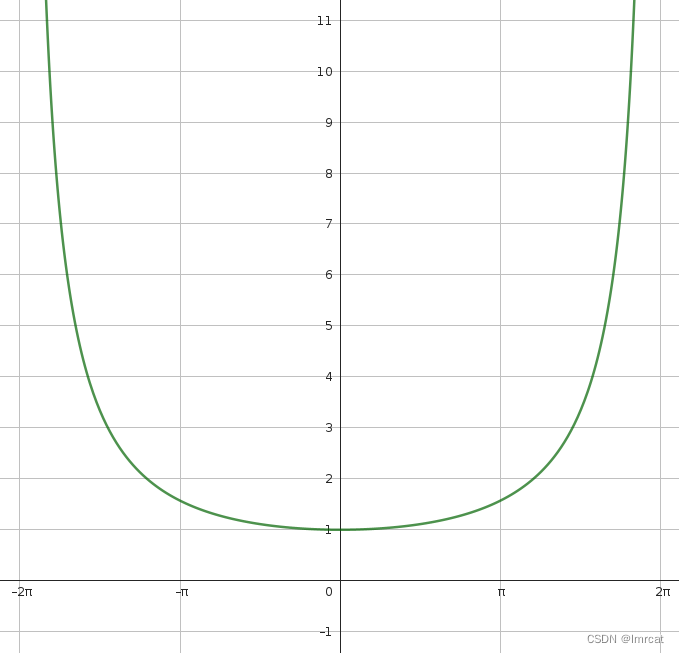
很明显，只有当 θ 趋近 0 时候，弧长才会近似等于弦长。

用求极限的方法也可以得到这个结论：

$\lim_{\theta \to0}{\frac{\theta}{2*sin(\frac{\theta}{2})}}= \frac{\frac{\theta}{2}}{sin(\frac{\theta}{2})} \iff \lim_{x \to0}{\frac{x}{sin(x)}}=1$

通过上面的分析可以知道 smac 曲率成本计算的前提条件有两个：

离散曲线点分布均匀，间距相等。
离散曲线点密集。

曲率成本函数为：

$Cost_{curvature} = (\frac{arccos(\frac{\overrightarrow{u} \cdot {\overrightarrow{v}}}{|\overrightarrow{u}||\overrightarrow{v}|})}{|\overrightarrow{u}|}-k_{max})^2$

$\overrightarrow {u}$ 是 pt_m -> pt 向量， $\overrightarrow {v}$ 是 pt -> pt_p 向量， $k_{max}$ 是限制的最大曲率。当超出曲率限制部分小于 0 时候成本为 0。

smac 用超出曲率限制部分的大小的平方作为惩罚，源码如下：

  inline void addCurvatureResidual(
    const double & weight,
    const Eigen::Vector2d & pt,
    const Eigen::Vector2d & pt_p,
    const Eigen::Vector2d & pt_m,
    CurvatureComputations & curvature_params,
    double & r) const
  {
    // pt_m -> pt -> pt_p
    curvature_params.valid = true;
    curvature_params.delta_xi = Eigen::Vector2d(pt[0] - pt_m[0], pt[1] - pt_m[1]);
    curvature_params.delta_xi_p = Eigen::Vector2d(pt_p[0] - pt[0], pt_p[1] - pt[1]);
    curvature_params.delta_xi_norm = curvature_params.delta_xi.norm();
    curvature_params.delta_xi_p_norm = curvature_params.delta_xi_p.norm();

    if (curvature_params.delta_xi_norm < EPSILON || curvature_params.delta_xi_p_norm < EPSILON ||
      std::isnan(curvature_params.delta_xi_p_norm) || std::isnan(curvature_params.delta_xi_norm) ||
      std::isinf(curvature_params.delta_xi_p_norm) || std::isinf(curvature_params.delta_xi_norm))
    {
      // ensure we have non-nan values returned
      curvature_params.valid = false;
      return;
    }

    // 矢量(pt - pt_m)和矢量(pt_p - pt)的夹角 cos 值
    const double & delta_xi_by_xi_p =
      curvature_params.delta_xi_norm * curvature_params.delta_xi_p_norm;
    double projection =
      curvature_params.delta_xi.dot(curvature_params.delta_xi_p) / delta_xi_by_xi_p;
    if (fabs(1 - projection) < EPSILON || fabs(projection + 1) < EPSILON) {
      projection = 1.0;
    }

    curvature_params.delta_phi_i = std::acos(projection); // 矢量夹角
    // 曲率 k = 转角 theta / 弧长 s，这里将向量模近似看做弧长
    curvature_params.turning_rad = curvature_params.delta_phi_i / curvature_params.delta_xi_norm;
    curvature_params.ki_minus_kmax = curvature_params.turning_rad - _params.max_curvature;

    if (curvature_params.ki_minus_kmax <= EPSILON) {
      // Quadratic penalty need not apply
      curvature_params.valid = false;
      return;
    }

    r += weight *
      curvature_params.ki_minus_kmax * curvature_params.ki_minus_kmax;  // objective function value
  }

curvature_params.turning_rad 是点 pt 位置的曲率，curvature_params.ki_minus_kmax 就是超出曲率限制部分的值，可以是负值，负值表示当前曲率还在限定范围内。

曲率成本梯度函数

根据链式法则，把曲率成本函数看做多个函数的复合，令

$x= \left[ \begin{matrix} x_{pt} \\ y_{pt} \end{matrix} \right]$

$i(x)=\overrightarrow{u} \cdot \overrightarrow{v}$

$j(x)=\frac{1}{|\overrightarrow{u}||\overrightarrow{v}|}$

$h(x)=i(x)*j(x)$ ，向量 u 和 v 的夹角 cos 值

$f(x)=arccos(h(x))$ ，向量 u 和 v 的夹角 θ

$g(x)=|\overrightarrow{u}|$ ，向量 u 的模

$m(x)= \frac{arccos(\frac{\overrightarrow{u} \cdot {\overrightarrow{v}}}{|\overrightarrow{u}||\overrightarrow{v}|})}{|\overrightarrow{u}|}-k_{max} =\frac{f(x)}{g(x)}-k_{max}$ ，曲率超限值函数

$n(x)=Cost_{curvature}=(m(x))^2$ ，曲率成本代价函数

复合函数求导

n(x) 求导

$\frac{\partial n}{\partial x}= \frac{\partial n}{\partial m} \frac{\partial m}{\partial x}= 2*m(x)*\frac{\partial m}{\partial x}= 2*curvatureDelta*\frac{\partial m}{\partial x}$

curvatureDelta 就是求导位置的曲率超限值，对应源码变量 curvature_params.ki_minus_kmax。

m(x) 求导

$\frac{\partial m}{\partial x}= \frac{\partial m}{\partial f} \frac{\partial f}{\partial x}+ \frac{\partial m}{\partial g} \frac{\partial g}{\partial x}= \frac{1}{|\overrightarrow u|}\frac{\partial f}{\partial x}+ \frac{\theta}{-|{\overrightarrow u|}^2} \frac{\partial g}{\partial x}= \frac{1}{|\overrightarrow u|}\frac{\partial f}{\partial x}- \frac{\theta}{|{\overrightarrow u|}^2} \frac{\partial g}{\partial x}$

$\overrightarrow {u}$ 是求导位置的向量（ptm 指向 pt），对应源码变量 curvature_params.delta_xi。

$|\overrightarrow {u}|$ 就是向量的模，对应源码变量 curvature_params.delta_xi_p_norm。

θ 是求导位置的向量 u 和 v 的夹角，对应源码变量 curvature_params.delta_phi_i。

把 $\frac{\partial m}{\partial x}$ 代入 $\frac{\partial n}{\partial x}$ ，有

$\frac{\partial n}{\partial x}= 2*curvatureDelta*(\frac{1}{|\overrightarrow u|}\frac{\partial f}{\partial x}- \frac{\theta}{|{\overrightarrow u|}^2} \frac{\partial g}{\partial x})$

g(x) 求导

$g(x)=|\overrightarrow u|=((x_{pt}-x_{ptm})^2+(y_{pt}-y_{ptm})^2)^{\frac{1}{2}}$ ，对 g(x) 偏求导有

$\begin{aligned} \frac{\partial g}{\partial x_{pt}} &= \frac{1}{2}((x_{pt}-x_{ptm})^2+(y_{pt}-y_{ptm})^2)^{-\frac{1}{2}}(2(x_{pt}-x_{ptm})) \\ &= \frac{1}{2}\frac{1}{|\overrightarrow{u}|}(2(x_{pt}-x_{ptm})) \\ &= \frac{x_{pt}-x_{ptm}}{|\overrightarrow{u}|} \end{aligned}$

$\begin{aligned} \frac{\partial g}{\partial y_{pt}} &= \frac{1}{2}((x_{pt}-x_{ptm})^2+(y_{pt}-y_{ptm})^2)^{-\frac{1}{2}}(2(y_{pt}-y_{ptm})) \\ &= \frac{1}{2}\frac{1}{|\overrightarrow{u}|}(2(y_{pt}-y_{ptm})) \\ &= \frac{y_{pt}-y_{ptm}}{|\overrightarrow{u}|} \end{aligned}$

$\begin{aligned} \frac{\partial g}{\partial x} &= [\frac{\partial g}{\partial x_{pt}}, \frac{\partial g}{\partial y_{pt}}] \\ &= [\frac{x_{pt}-x_{ptm}}{|\overrightarrow{u}|}, \frac{y_{pt}-y_{ptm}}{|\overrightarrow{u}|}] \\ &= \frac{1}{|\overrightarrow{u}|} [x_{pt}-x_{ptm}, y_{pt}-y_{ptm}] \\ &= \frac{\overrightarrow u}{|\overrightarrow{u}|} \end{aligned}$

把 $\frac{\partial g}{\partial x}$ 代入 $\frac{\partial n}{\partial x}$ ，有

$\frac{\partial n}{\partial x}= 2*curvatureDelta*(\frac{1}{|\overrightarrow u|}\frac{\partial f}{\partial x}- \frac{\theta}{|{\overrightarrow u|}^2} \frac{\overrightarrow u}{|\overrightarrow{u}|})$

这里可以看出，向量的模求导得到向量的方向，向量的方向则用单位向量表示。

f(x) 求导

$\frac{\partial f}{\partial x}= \frac{\partial f}{\partial h} \frac{\partial h}{\partial x}= -\frac{1}{\sqrt{1-cos^2(\theta)}} \frac{\partial h}{\partial x}$

把 $\frac{\partial f}{\partial x}$ 代入 $\frac{\partial n}{\partial x}$ ，有

$\frac{\partial n}{\partial x}= 2*curvatureDelta*(\frac{1}{|\overrightarrow u|}(-\frac{1}{\sqrt{1-cos^2(\theta)}})\frac{\partial h}{\partial x}- \frac{\theta}{|{\overrightarrow u|}^2} \frac{\overrightarrow u}{|\overrightarrow{u}|})$

i(x) 求导

$\begin{aligned} i(x) &=\overrightarrow u \cdot \overrightarrow v \\ &= (x_{pt}-x_{pm})(x_{ptp}-x_{pt})+(y_{pt}-y_{pm})(y_{ptp}-y_{pt}) \\ &=x_{pt}x_{ptp}-x_{pt}^2-x_{pm}x_{ptp}+x_{pt}x_{pm}+ y_{pt}y_{ptp}-y_{pt}^2-y_{pm}y_{ptp}+y_{pt}y_{pm} \end{aligned}$

对 i(x) 偏求导有

$\frac{\partial i}{\partial x_{pt}}= x_{ptp}-2*x_{pt}+x_{pm}= (x_{ptp}-x_{pt})-(x_{pt}-x_{pm})= x_{\overrightarrow v}-x_{\overrightarrow u}$

$\frac{\partial i}{\partial y_{pt}}= y_{ptp}-2*y_{pt}+y_{pm}= (y_{ptp}-y_{pt})-(y_{pt}-y_{pm})= y_{\overrightarrow v}-y_{\overrightarrow u}$

$\frac{\partial i}{\partial x}= [x_{\overrightarrow v}-x_{\overrightarrow u}, \ y_{\overrightarrow v}-y_{\overrightarrow u} ]=\overrightarrow v - \overrightarrow u$

j(x) 求导

根据前面对矢量的模求导的结论，有

$\begin{aligned} \frac{\partial j}{\partial x} &= \frac{({|\overrightarrow u||\overrightarrow v|})^{-1}} {\partial x} \\ &= -\frac{\overrightarrow u}{|\overrightarrow u|}{|\overrightarrow u|}^{-2}{|\overrightarrow v|}^{-1}-\frac{\overrightarrow v}{|\overrightarrow v|}{|\overrightarrow v|}^{-2}{|\overrightarrow u|}^{-1} \\ &= \frac{-1}{|\overrightarrow u||\overrightarrow v|}(\overrightarrow u*{(|\overrightarrow u|})^{-2}+ \overrightarrow v*{(|\overrightarrow v|})^{-2}) \end{aligned}$

h(x) 求导

$\frac{\partial h}{\partial x}= \frac{\partial h}{\partial i} \frac{\partial i}{\partial x}+ \frac{\partial h}{\partial j} \frac{\partial j}{\partial x}= j(x)*\frac{\partial i}{\partial x}+ i(x)*\frac{\partial j}{\partial x}= \frac{1}{|\overrightarrow u||\overrightarrow v|}*\frac{\partial i}{\partial x}+(\overrightarrow u \cdot \overrightarrow v)*\frac{\partial j}{\partial x}$

把 $\frac{\partial i}{\partial x}$ 和 $\frac{\partial j}{\partial x}$ 代入 $\frac{\partial h}{\partial x}$ ，有

$\frac{\partial h}{\partial x}= \frac{1}{|\overrightarrow u||\overrightarrow v|}* (\overrightarrow v - \overrightarrow u)+(\overrightarrow u \cdot \overrightarrow v)* (\frac{-1}{|\overrightarrow u||\overrightarrow v|}(\overrightarrow u*{(|\overrightarrow u|})^{-2}+ \overrightarrow v*{(|\overrightarrow v|})^{-2}))$

再把 $\frac{\partial h}{\partial x}$ 代入 $\frac{\partial n}{\partial x}$ 就能够得到完整的曲率成本梯度函数，完整公式太长了这里就不写了。

！！！注意！！！

h(x) 的求导公式是唯一与 smac 源码（foxy版本）不符合的地方。

源码的公式根据代码反过来推算大概如下：

$\begin{aligned} \frac{\partial h}{\partial x}= \frac{-1}{|\overrightarrow u||\overrightarrow v|}* (\overrightarrow {-ptp} + \overrightarrow {pt})-(\overrightarrow {pt} \cdot \overrightarrow {-ptp})* (\frac{-1}{|\overrightarrow u||\overrightarrow v|}(\overrightarrow {pt}*{(|\overrightarrow {pt}|})^{-2}+ \overrightarrow {-ptp}*{(|\overrightarrow {-ptp}|})^{-2})) \end{aligned}$

这里丢失了向量 u 比较奇怪，因为 pt 与两个向量 u 和 v 都是有关联的。

源码：

  inline Eigen::Vector2d derivation_hx( // 本文对 h(x) 函数的求导
    const Eigen::Vector2d & a,
    const Eigen::Vector2d & b,
    const double & a_norm,
    const double & b_norm) const
  {
    Eigen::Vector2d prefix = (b-a)/(a_norm*b_norm);
    Eigen::Vector2d suffix = (a.dot(b)*(-(a*a.squaredNorm()+b*b.squaredNorm())))/(a_norm*b_norm);
    return prefix + suffix;
  }
  
  inline void addCurvatureJacobian(
    const double & weight,
    const Eigen::Vector2d & pt,
    const Eigen::Vector2d & pt_p,
    const Eigen::Vector2d & /*pt_m*/,
    CurvatureComputations & curvature_params,
    double & j0,
    double & j1) const
  {
    if (!curvature_params.isValid()) {
      return;
    }

    const double & partial_delta_phi_i_wrt_cost_delta_phi_i =
      -1 / std::sqrt(1 - std::pow(std::cos(curvature_params.delta_phi_i), 2));

    Eigen::Vector2d p3 = derivation_hx(curvature_params.delta_xi,
      curvature_params.delta_xi_p, curvature_params.delta_xi_norm, curvature_params.delta_xi_p_norm);

    const double & u = 2 * curvature_params.ki_minus_kmax;
    const double & common_prefix =
      (1 / curvature_params.delta_xi_norm) * partial_delta_phi_i_wrt_cost_delta_phi_i;
    const double & common_suffix = curvature_params.delta_phi_i /
      (curvature_params.delta_xi_norm * curvature_params.delta_xi_norm);

    const Eigen::Vector2d & d_delta_xi_d_xi = curvature_params.delta_xi /
      curvature_params.delta_xi_norm;

    const Eigen::Vector2d jacobian = u *
      ((common_prefix * p3) - (common_suffix * d_delta_xi_d_xi));
    j0 += weight * jacobian[0];  // xi x component of partial-derivative
    j1 += weight * jacobian[1];  // xi x component of partial-derivative
  }