熵(Entropy)：衡量混乱与秩序

最新推荐文章于 2025-05-02 23:00:47 发布

懒麻蛇

最新推荐文章于 2025-05-02 23:00:47 发布

阅读量2.4k

点赞数 27

文章标签：人工智能算法机器学习

本文链接：https://blog.csdn.net/lazysnake666/article/details/142907808

版权

本文是Rami Khushaba视频《Measuring Signal Complexity/Regularity》的笔记，内容略有补充，推荐看视频。

熵是一个重要的概念，它帮助量化系统的无序或混乱程度。通过了解熵，可以深入认识诸如脑电图（EEG）、心电图（ECG）等生理信号的动态特性。

1. 什么是熵？

熵（Entropy）最早由克劳修斯提出，是一个用来描述系统“混乱”或“不确定性”的指标。熵可以看作是信息缺乏的程度。系统越不确定，熵就越高；反之，系统越有序，熵就越低。

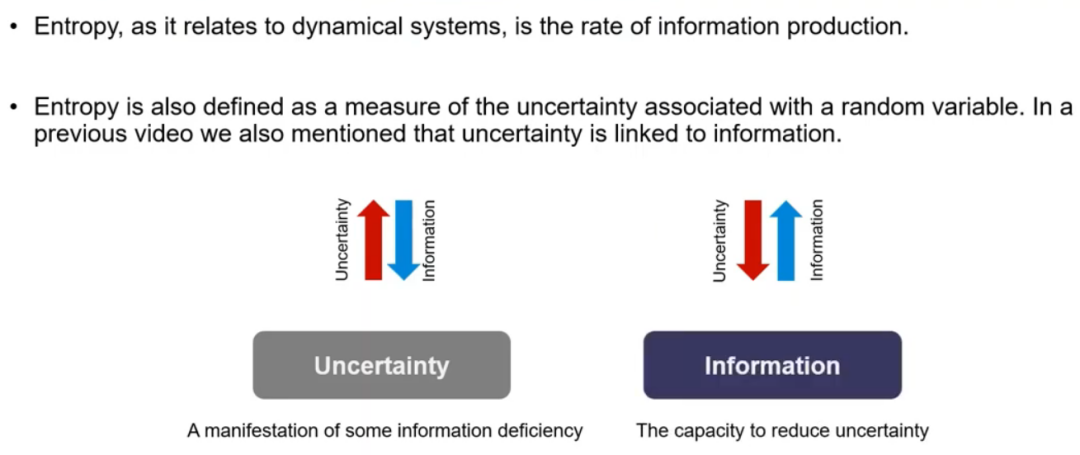
这里介绍了几种常用于分析时间序列数据的熵度量方法，包括：

近似熵（Approximate Entropy, ApEn）
样本熵（Sample Entropy, SampEn）
模糊熵（Fuzzy Entropy, FuzzyEn）
分布熵（Distribution Entropy, DistEn）
置换熵（Permutation Entropy, PermEn）

这些方法不仅可以应用于生理信号，还能用在其他任何类型的时间序列数据上。

2. 嵌入维度

在介绍具体的熵之前，需要知道什么是嵌入维度（embedding dimension）和距离计算。

嵌入维度是用于将时间序列重构为相空间表示的参数，表示构建数据点向量时所使用的连续数据点的数量。嵌入维度的选择对于捕捉信号的动态特性非常重要。具体来说，嵌入维度决定了在时间序列中，每个时刻需要多少个数据点来构建一个多维向量，以便更好地反映系统的状态。

如果嵌入维度过小，可能无法充分捕捉到信号的复杂性；而如果嵌入维度过大，则可能导致冗余并增加计算复杂度。因此，嵌入维度是平衡信号复杂性和计算效率的重要参数。

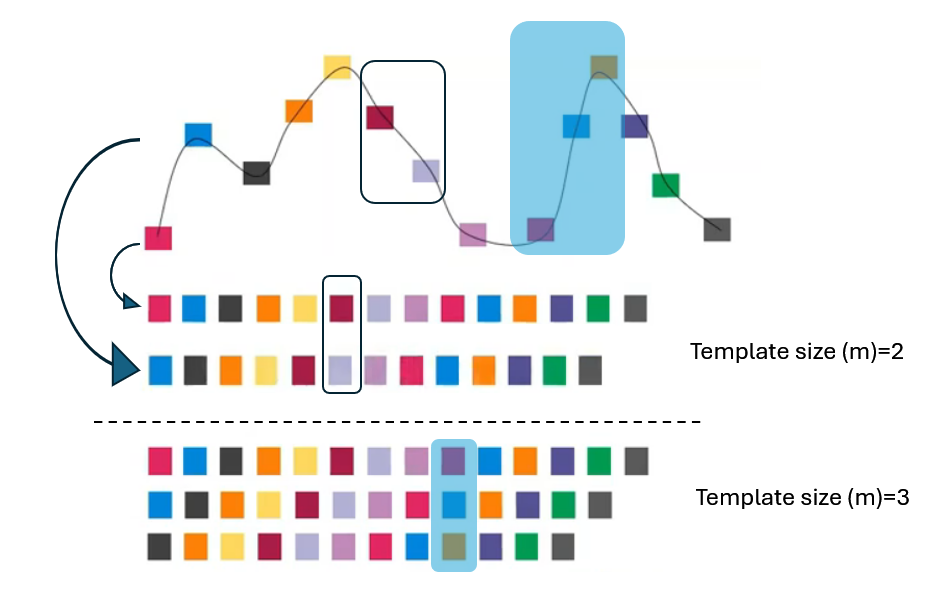
比如有一个时间序列，首先从第一个点开始，将后续数据点排列成一个向量，然后从第二个点开始，将后续数据点排列成另一个向量，以此类推，构建出多个向量。图中显示了模板大小（m=2 & m=3）和时间延迟（τ=1）的过程，每个颜色方块代表一个数据点，通过滑动窗口的方式构建嵌入空间（embedding dimension）。这样可以更方便地捕捉时间序列中的动态特性，方便后续距离的计算。

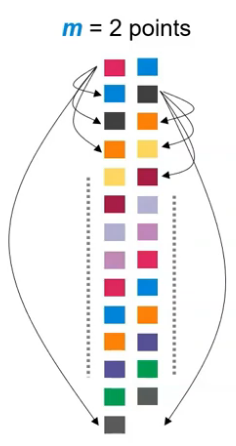
例如，这里m=2时，我们计算每一个配对和其他配对距离时，试图找到的是时间序列数据中每个m=2可能的模板和其他数据的相似程度(距离)。

对于嵌入维度m=2，在计算时间序列的最后一个点的嵌入向量时，由于我们每次向前移动一个点（即时间延迟τ=1），当移动到最后时，会出现嵌入向量不完整的情况。具体来说，对于时间序列中的最后一个点，缺少足够的数据来形成一个完整的嵌入向量。

通常，这种情况下有以下几种处理方式：

忽略不完整的嵌入向量：最常见的方法是忽略那些由于缺少足够数据而无法构建的嵌入向量。在这种情况下，距离计算只包括那些可以构成完整向量的部分。例如，最后的一个点没有足够的数据去构建第二个嵌入维度的向量，因此就不参与距离计算。
例如：(最后Permutation entropy的例子中)
模板大小m=3，时间延迟τ=1。将时间序列S(t)={4,7,9,10,6,11,3}划分为长度为m的嵌入向量。通过时间延迟τ，逐次得到多个嵌入向量。
忽略不完整的行，得到如下矩阵；
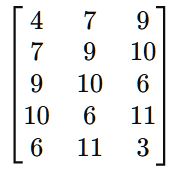
循环补全（周期性补全）：有时可以采用周期性补全的方式，将时间序列看作是循环的，从头部补充到尾部。例如，缺少的数据可以用序列开头的数据来补全。这种方法适用于那些具有明显周期性的信号，但可能不适用于大多数非周期性的时间序列。
数据插值：另一种方法是使用插值（如线性插值）来填补缺失值，以构建完整的嵌入向量。不过，插值可能会引入一些估计误差，尤其是信号具有复杂动态特性时。

通常会选择忽略不完整的嵌入向量，来确保计算的准确性。即只计算那些具有足够点数的嵌入向量之间的距离。这样可以避免引入不确定的估计误差，同时保持嵌入分析的严谨性。

距离的计算很简单，就不详述了。

3. 近似熵：从混乱中寻找规律

近似熵（Approximate Entropy, ApEn）是一种用于量化时间序列数据混乱程度的方法，由Pincus提出，用于测量系统的复杂性和规律性。其目标是用一个数值来描述信号的“可预测性”或“混乱程度”。如果信号非常有规律，如正弦波，近似熵值就会接近零；而当信号越混乱，近似熵就越大。

近似熵通过对时间序列的不同片段进行比较，找到相似的模式并计算其出现的概率来确定信号的规律性。近似熵的计算步骤可以总结为：

选择模板长度m 和容差r。
构建嵌入维度为m 和m+1 的嵌入向量。
计算嵌入向量之间的距离，并确定相似性。
通过对比不同嵌入维度下相似模板的数量，计算近似熵，以评估信号的复杂性。

计算公式：

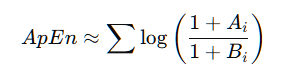
Ai：与第i 个模板（嵌入维度为m+1）相似的嵌入向量的数量。
Bi：与第 i 个模板（嵌入维度为m）相似的嵌入向量的数量。
加1 是为了避免出现对零取对数的情况。

这个公式用于比较嵌入维度m 和m+1 时相似模板的数量。如果在增加维度后相似性显著减少，说明信号的复杂性较高，因此近似熵的值较大；反之，若相似性变化不大，说明信号较有规律，近似熵较小。

例如：

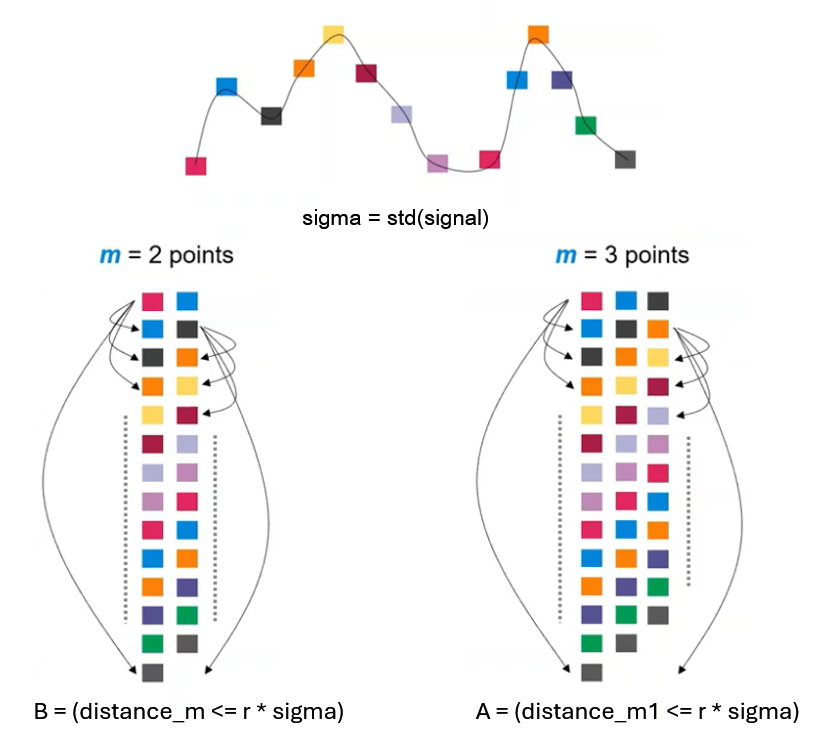
对于m=2和m=3，分别计算其具有相似性模式，相似性根据容差r和信号的标准差sigma (r*sigma为阈值)来确定。嵌入维度越大，描述信号动态行为的能力就越强，但相应地匹配的相似片段数量会减少。通过计算不同嵌入维度下的距离，观察在增加维度后，相似模式的变化情况。这种方法可以量化信号的可预测性和复杂性。

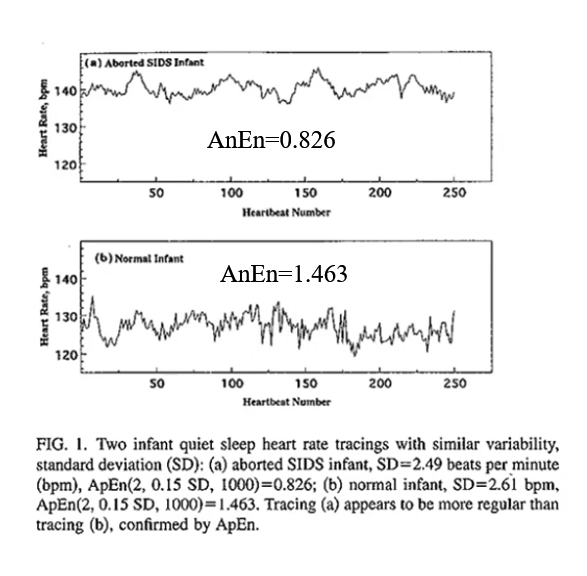
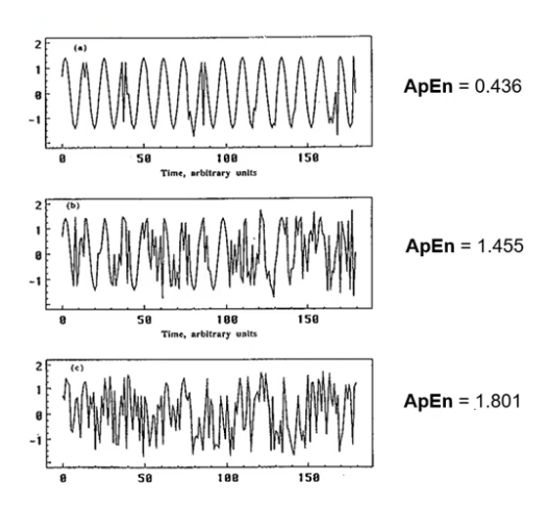
Pincus (1994)

在近似熵（Approximate Entropy, ApEn）计算中可能遇到的一些问题

a. 如何选择 m 和 r

在近似熵的计算过程中，选择合适的参数m 和r 是至关重要的。m 的选择会影响嵌入向量的长度，而r的选择会影响相似模板的数量，这两个参数的选择直接决定了最终的熵值。

选择模板长度m：通常建议模板长度m 取 1 或 2。这样做的目的是保证有足够多的模板匹配，减少由于模板数量不足导致的偏差。选择m=1 时，偏差较少，但对于揭示信号的动态特性可能不足。而选择m=2或更大的值，则可以揭示更多关于信号的复杂性和动态特征，但匹配的模板数量可能会减少。
选择容差r：通常的建议是将容差rrr 设为信号标准差 (SD) 的 0.2 倍，即r=0.2×SD。这种经验性的选择可以有效平衡模板匹配的数量，使得熵值的估计更稳定。

b. 模板匹配数量较少或没有匹配

在实际计算中，有时可能会出现某些模板没有任何匹配的情况。这意味着条件概率为 1（这里得到1可能是因为存在模板和自己计算距离为0，卡阈值后是1)，导致近似熵 ApEn 的值为 0。熵值为 0 意味着信号是完全有序的（perfect order）。这种情况可能会导致对信号复杂性的误判，因此在计算中需要特别注意避免这种情况。

当模板匹配的数量非常少时，计算结果会出现偏向于 0 的情况，即熵值会趋于更小的值。这是因为在匹配模板的数量不足时，近似熵的计算公式中的对数值趋于较小，进而导致偏差。这种偏差可以通过延长数据序列和增加模板匹配数量来解决。

尽管近似熵存在这种偏差，文献中指出，重要的是保留正确的阶层次序。这意味着近似熵可以用来描述不同信号之间的相对复杂性，而不仅仅关注绝对值大小。因此，近似熵仍然保留了描述复杂性的一种特性，即相对一致性（relative consistency）。

4. 样本熵：减少偏差的改进

样本熵（Sample Entropy, SampEn）是对近似熵的改进，解决了近似熵在计算中可能遇到的偏差问题。样本熵具有两个主要优点：对数据长度的依赖性更小，更适合用于长度不等的时间序列数据；此外还减少了近似熵中的自我偏差问题。

在计算样本熵时，同样选择一个模板长度m，并将其与信号的其他部分进行比较。样本熵的计算公式为：

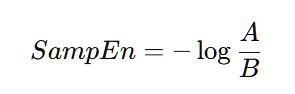
其中，A表示模板长度为m+1时相似片段的数量，B表示模板长度为m时相似片段的数量。样本熵的直观理解是，如果信号越混乱，相似片段的数量就越少，样本熵的值就会增大。

相比于近似熵，先计算相似模板的数量。

近似熵：

A=(distance_m1<=r*sigma)

B=(distance_m<=r*sigma)

样本熵:

A=sum(distance_m1<=r*sigma)

B=sum(distance_m<=r*sigma)

在近似熵中，每个嵌入向量会与其他嵌入向量进行比较，并且每次的匹配数量会被作为概率进行计算，然后将这些概率值相加。由于取对数的计算，近似熵的结果可能会偏向于一个值，尤其在数据不充分时，这会使得近似熵值过低。

样本熵则简化了匹配的计算，直接对相似片段的总数进行求和，最后通过一个对数来计算整体的熵值。这使得计算更加稳定，并且减少了近似熵中频繁的对数操作所可能引入的偏差。

如果还不太理解它们的差异，请注意近似熵计算公式中的求和符号Σ！

以下的样本熵的例子：

Víctor Martínez-Cagigal (2018). Sample Entropy. Mathworks.

和近似熵类似，同样面临参数选择的问题：

参数m 的选择

m取值过大：
- 当嵌入维度m 取值过大时，模板匹配的数量会减少。这是因为嵌入维度越大，每个嵌入向量包含的点越多，由于测量误差或系统相互作用中的噪声影响，找到匹配的可能性变得更小。因此，匹配的模板数量会减少，可能导致熵值的准确性下降。
m 取值过小：
- 当嵌入维度m 取值过小时，模板匹配的数量会非常多（即匹配的数量BBB 较大），但嵌入向量过短，可能不足以捕捉信号中的复杂动态特征。这会导致对信号复杂性的低估，因为短的嵌入向量无法包含足够的预测信息，从而低估了向前匹配的概率。

参数r 的选择

r 取值过大：
- 当容差r 取值过大时，几乎所有嵌入向量之间的距离都会落在容差范围内，导致大部分模板看起来都是相似的。这种情况下，熵的判别能力（discriminating power）会完全丧失，因为熵无法有效地区分不同信号的复杂性，所有模板的相似性都会被高估。
r 取值过小：
- 当容差r 取值过小时，会导致本来相似的嵌入向量无法被匹配。即使两个嵌入向量实际上非常接近，但由于容差过小，它们可能仍无法满足相似性的条件，从而导致匹配的数量过少，熵值可能无法准确反映信号的实际复杂性。

简而言之：嵌入维度m 不能太大，否则匹配数量过少，导致熵值不稳定；也不能太小，否则无法捕捉到足够的动态特征，导致复杂性被低估。容差 r 如果过大，所有向量都会相似，失去区分力；如果过小，很多相似的向量会被误认为不同，无法正确反映信号的复杂性。

5. 模糊熵：把相似性映射到高斯分布中

模糊熵（Fuzzy Entropy, FuzzyEn）进一步将“不确定性”带入熵的定义中。现实中的生理信号通常不会明确地属于某个特定的状态，而是介于多个状态之间，这就体现了信号的模糊性。因此，模糊熵不再使用“0或1”这样绝对的判断标准，而是通过对相似性度量进行模糊处理，从而更精确地反映信号的复杂性。

模糊熵则采用了“模糊隶属度函数”（fuzzy membership function），这种函数允许计算相似性概率，具有更连续和平滑的特性，而不是简单的“1”或“0”。

模糊熵的计算公式为：

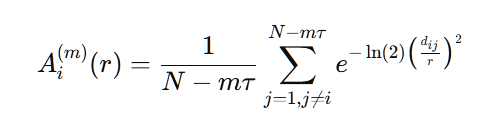
公式中的dij 表示第i 和第j 个嵌入向量之间的距离。
隶属度函数的形式是一个指数函数，它将距离dij映射到相似性度量，使用的是一个模糊化的高斯函数形式。这种方式使得即使嵌入向量的距离略微超过阈值r，它们之间的相似性也不会直接降为 0，而是以平滑的方式减小。

模糊熵的优点

连续的相似性度量：模糊熵通过模糊隶属度函数提供了一种连续的相似性度量，相较于样本熵中硬阈值的判断方式，模糊熵能够更好地反映相似性的渐变。这种方法在面对噪声较多的数据时具有更强的鲁棒性。
减少对阈值的敏感性：由于相似性是基于模糊隶属度函数，而不是简单的是否小于阈值 r，模糊熵在选择参数 r 时的敏感性较低。因此，即使容差 r 选择得不够精确，模糊熵的值仍能较好地反映信号的复杂性。

6. 分布熵：使用距离分布描绘复杂度

分布熵（Distribution Entropy, DistEn）是一种基于概率分布的复杂性度量方法，用于描述时间序列的动态行为。与样本熵、模糊熵等不同，分布熵通过分析信号中嵌入向量之间距离的分布情况，量化信号的复杂性。其核心思想是利用直方图来统计嵌入向量之间的距离，并通过计算概率分布的熵值来衡量信号的复杂性。

计算步骤

计算距离向量的最小值和最大值：
从时间序列中计算出所有嵌入向量之间的距离。可以使用例如 pdist 这样的函数来计算得到距离矩阵，其中包含了所有向量之间的两两距离。从这些距离中找到最小值（min）和最大值（max），并计算距离范围（range），即 (max−min)。
选择直方图的区间数量：
选择一个合适的直方图区间数（bins），例如可以选择 10 个区间。将整个距离范围划分为这些区间，例如 (max−min)/10，这样就得到了每个区间的宽度。
生成直方图并计算概率：
将所有距离值划分到选定的区间中，然后统计每个区间中包含的距离值数量。接下来，将每个区间的数量除以总的距离数量，得到每个区间的概率pt。这些概率构成了一个分布，用于描述嵌入向量之间距离的频率分布。

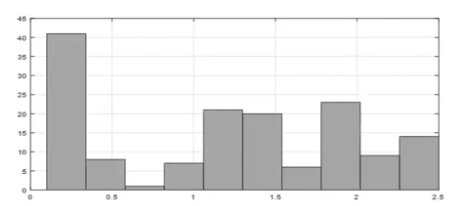
d. 然后通过公式进行计算：

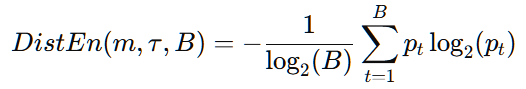
B是直方图的区间数，pt 是第t 个区间中的概率。通过计算这些概率的对数加权和，可以得到整个信号的分布熵值。

具体应用的例子：

该研究使用的EEG数据来自公开的Bonn数据库，包含500个单通道记录，每个记录采样频率为173.61 Hz，持续23.6秒，分为Z、O、N、F和S五类，各类有100个记录。Z和O类数据是从五位健康志愿者在清醒放松状态下采集的，其中Z类是睁眼状态，O类是闭眼状态；N、F和S类则是从五位癫痫患者采集的，分别记录于病灶对侧半球（间歇期）、病灶半球（间歇期）和发作期。所有EEG记录在分析前均经过20阶FIR带通滤波（0.53-40 Hz）处理。

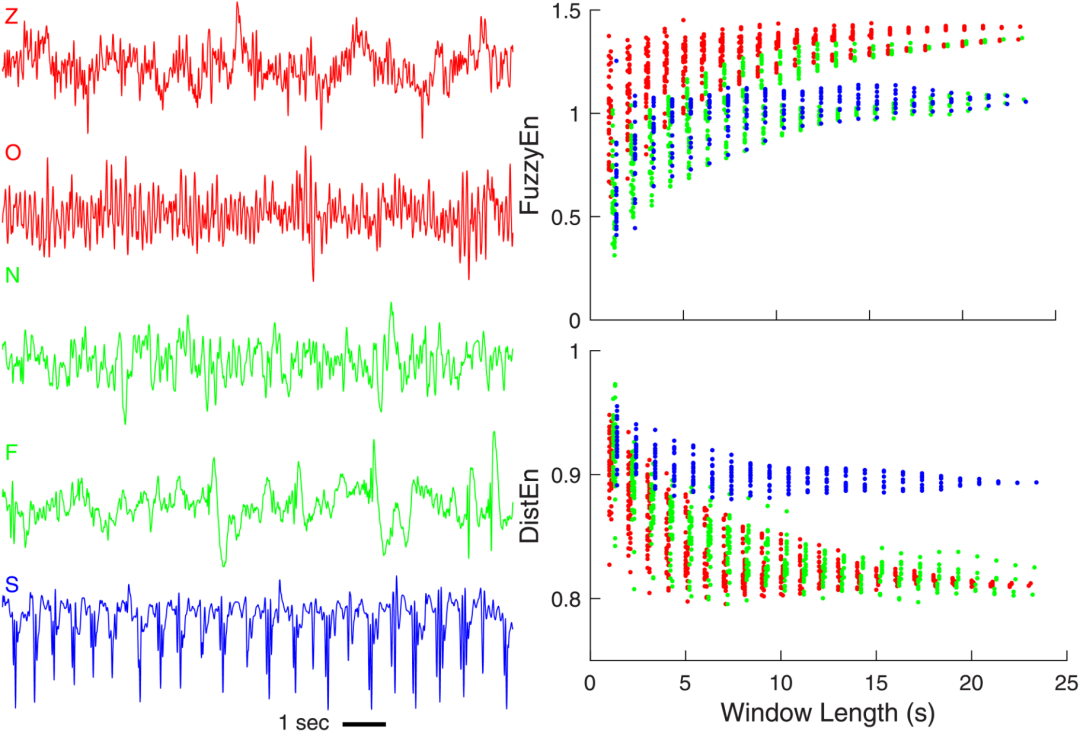
图中看出DisEn相比于FuzzyEn能有效区分S类(发作期癫痫患者)

(Li 2018 Plos One)

6. 置换熵：从排序中看复杂性

置换熵（Permutation Entropy, PermEn）是一种简单但有效的熵度量方法，通过分析时间序列中数值的排列顺序来衡量复杂性。首先，将时间序列分割为若干段，每段按照数值大小排序，并统计各个排序模式的出现频率。

特点：

非参数方法：置换熵是一种非参数方法，它不依赖于参数化模型的假设，这使得它在应用中更加灵活。
对噪声鲁棒：置换熵对噪声具有鲁棒性，计算效率高，并且对数据的非线性单调变换不敏感。这意味着它在处理非线性时间序列数据时可以保持良好的性能。
基于顺序的测量：置换熵依赖于熵和符号动态的概念，专注于数据的顺序排列来进行复杂性评估。它考虑了时间序列的时间因果性，即时间顺序结构，通过分析信号的值的顺序变化来评估复杂性。
复杂性量化：这种方法允许用户解锁非线性时间序列中的复杂动态信息，特别适用于动态系统的复杂性测量。

计算：

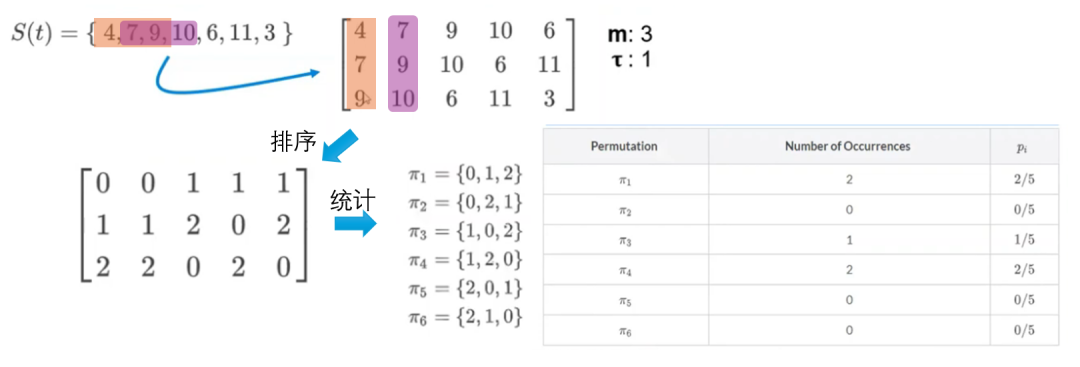
选择模板大小和时间延迟，生成嵌入矩阵：
模板大小 m=3，时间延迟 τ=1。将时间序列 S(t)={4,7,9,10,6,11,3}划分为长度为 m的嵌入向量。通过时间延迟 τ，逐次得到多个嵌入向量。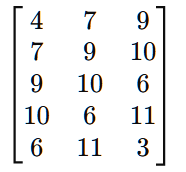为了方便排序和计算，对其做转置
映射到排列模式：
通过比较嵌入向量中数值的大小，将每个向量映射到相应的排列模式。例如，对于向量{4,7,9}，其排列模式为{0,1,2}，表示从小到大的顺序。重复这一过程，对每个嵌入向量计算其排列模式。
计算相对频率：
统计每个排列模式的出现次数，并计算相对频率。例如，排列模式π1 出现了 2 次，因此其概率为2/5。通过计算所有排列模式的相对频率，可以得到每种顺序的概率分布。
计算置换熵：
最终，根据所有排列模式的相对频率 pi 计算置换熵：
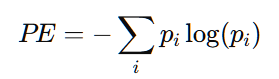
这个熵值表示时间序列中顺序模式的复杂程度，越高的置换熵值意味着信号越混乱和不规则。

7.EntropyHub

在实际分析时间序列数据的过程中，选择合适的熵度量方法至关重要。EntropyHub 是一个开源工具箱，专门用于熵分析，支持多种时间序列的复杂性度量。它包括了丰富的熵类型和相应的函数，方便研究者根据不同的需求来进行数据分析。

EntropyHub 工具箱提供了：

a. 基本熵（Base Entropies）：包含了近似熵（ApEn）、样本熵（SampEn）、模糊熵（FuzzEn）、分布熵（DistEn）等基本的熵度量方法。

b. 交叉熵（Cross Entropies） 是一种用于比较两个时间序列之间相似性的方法。具体而言，交叉熵通过衡量一个时间序列与另一个时间序列的同步或相似程度来量化它们之间的关系。交叉熵的常见应用场景包括：

生理信号之间的关联分析：例如，研究心率变异性和脑电信号之间的关系。
系统同步性分析：检测两个系统是否同步变化。

交叉熵包括交叉样本熵（Cross Sample Entropy, XSampEn）、交叉近似熵（Cross Approximate Entropy, XApEn）、交叉模糊熵（Cross Fuzzy Entropy, XFuzzEn）等。

c. 二维熵（Bidimensional Entropies） 是一种针对二维信号的复杂性分析方法。二维信号可能来自图像数据或者多通道的时间序列数据。二维熵的计算通过在二维的嵌入空间中进行度量，从而捕捉信号中的复杂性和关联特征。它们适用于：

图像处理和分析：例如在医学图像或遥感图像的纹理分析中使用二维熵。
多通道信号：如脑电图（EEG）中同时采集多个电极信号的数据分析。

二维熵度量包括二维样本熵（Bidimensional Sample Entropy, SampEn2D）、二维模糊熵（Bidimensional Fuzzy Entropy, FuzzEn2D）等。

d. 多尺度熵（Multiscale Entropy, MSE） 是为了在不同时间尺度上度量时间序列信号的复杂性而设计的。与传统熵方法只在一个时间尺度上分析信号不同，多尺度熵通过对时间序列进行多次重构和抽象，以观察在不同时间尺度下的信号复杂性。这对于理解信号在不同频率成分上的行为特别有用。主要应用场景包括：