pytorch 的二维卷积 torch.Conv2d，宽高计算公式如下所示（假设宽高相同，这里只讨论宽的公式，高的公式类似）：
W o u t = W i n + 2 × p a d d i n g − d i l a t i o n × ( k e r n e l s i z e − 1 ) − 1 s t r i d e + 1 W_{out} = \frac{W_{in} + 2 \times \mathrm{padding} - \mathrm{dilation} \times (\mathrm{kernelsize}-1)-1}{\mathrm{stride}} + 1 Wout=strideWin+2×padding−dilation×(kernelsize−1)−1+1
其中 dilation 为膨胀系数，kernel size 为 卷积核大小，一个膨胀系数为 2 的效果如下动图所示：
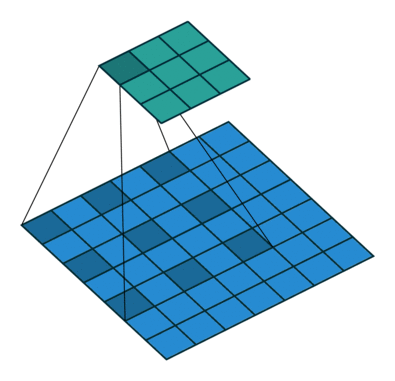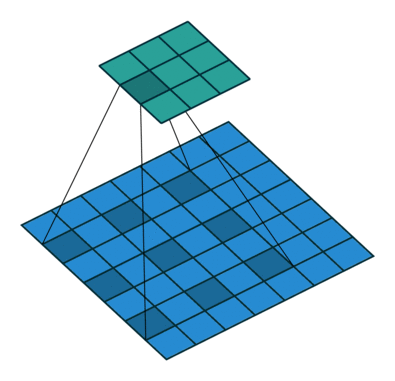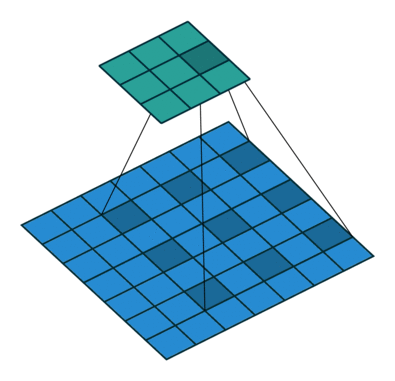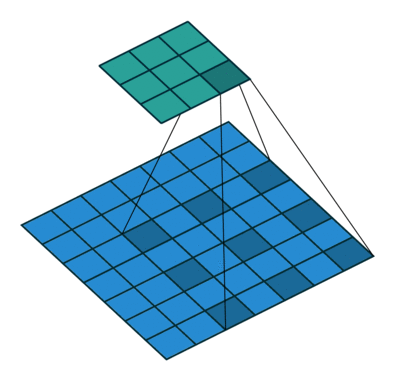
由此可见，一个膨胀系数为
d
d
d 的卷积核的感受野范围是
d
×
(
k
s
−
1
)
+
1
\mathrm{d} \times (\mathrm{ks} -1) + 1
d×(ks−1)+1，例如一个膨胀系数为 2 的
3
×
3
3 \times 3
3×3 卷积核，其感受野范围是
5
×
5
（
2
∗
2
+
1
）
5 \times 5（2 * 2 + 1）
5×5（2∗2+1）。所以感受野宽度为
W
r
f
=
d
i
l
a
t
i
o
n
×
(
k
e
r
n
e
l
s
i
z
e
−
1
)
+
1
W_\mathrm{rf}=\mathrm{dilation} \times (\mathrm{kernelsize}-1)+1
Wrf=dilation×(kernelsize−1)+1。上述宽高公式变形后为
W
o
u
t
=
W
i
n
+
2
×
p
a
d
d
i
n
g
−
(
d
i
l
a
t
i
o
n
×
(
k
e
r
n
e
l
s
i
z
e
−
1
)
+
1
)
s
t
r
i
d
e
+
1
=
W
i
n
+
2
×
p
a
d
d
i
n
g
−
W
r
f
s
t
r
i
d
e
+
1
\begin{aligned} W_{out} &= \frac{W_{in} + 2 \times \mathrm{padding} - (\mathrm{dilation} \times (\mathrm{kernelsize}-1)+1)}{\mathrm{stride}} + 1 \\ &=\frac{W_{in} + 2 \times \mathrm{padding} - W_\mathrm{rf}}{\mathrm{stride}} + 1 \end{aligned}
Wout=strideWin+2×padding−(dilation×(kernelsize−1)+1)+1=strideWin+2×padding−Wrf+1
当膨胀系数
d
=
1
d=1
d=1 时，感受野宽度
W
r
f
=
k
e
r
n
e
l
s
i
z
e
W_\mathrm{rf}=\mathrm{kernelsize}
Wrf=kernelsize，当
p
a
d
d
i
n
g
=
0
\mathrm{padding} = 0
padding=0 时，上述式子为
W
o
u
t
=
W
i
n
−
k
e
r
n
e
l
s
i
z
e
s
t
r
i
d
e
+
1
W_{out} = \frac{W_{in} - \mathrm{kernelsize}}{\mathrm{stride}} + 1
Wout=strideWin−kernelsize+1
默认参数 stride=1, padding=0, dilation=1 下的公式为
W
o
u
t
=
W
i
n
−
k
e
r
n
e
l
s
i
z
e
+
1
W_{out}=W_{in}-\mathrm{kernelsize} + 1
Wout=Win−kernelsize+1
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
