标准正态分布的积分求解如下:
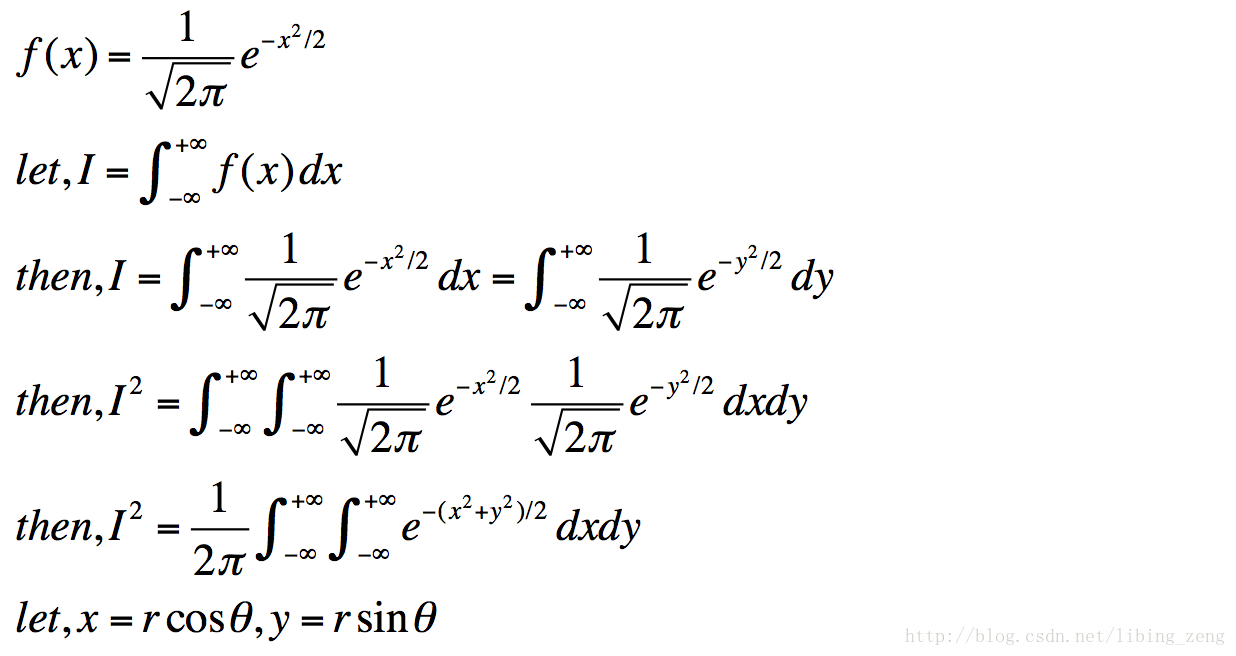
x=rcosθ y=rsinθ
是二重积分极坐标代换
而dxdy,rdrdθ是积分分别在直角坐标系和极坐标系的面积元素
当重积分从直角坐标向极坐标转换的时候要乘上一个雅克比行列式的绝对值
标准正态分布的积分求解如下:
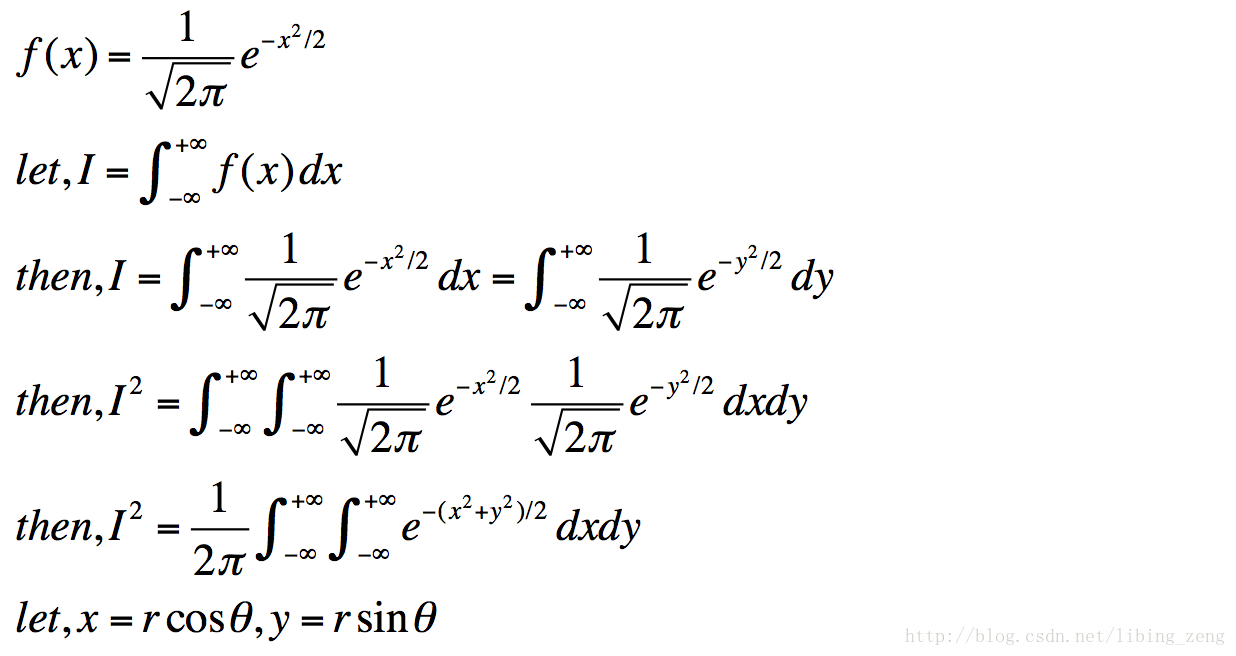
x=rcosθ y=rsinθ
是二重积分极坐标代换
而dxdy,rdrdθ是积分分别在直角坐标系和极坐标系的面积元素
当重积分从直角坐标向极坐标转换的时候要乘上一个雅克比行列式的绝对值
 9790
9790
 325
325
 10万+
10万+
 9846
9846

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


