[足式机器人]Part2 Dr. CAN学习笔记-Ch04 Advanced控制理论

本文仅供学习使用
本文参考：
B站：DR_CAN
控制之美（卷1）

---

1. 绪论

通过研究动态系统的数学模型和系统表现，可以得到在给定输入$u(t)$作用下的系统响应(Response,即系统在输入$u(t)$作用下的输出$x(t)$)。当掌握了动态系统输入与输出的关系之后，就可以设计控制器来调节动态系统的输入，使得系统的输出按照预期的目标响应。

一般而言，控制系统(Control System)由控制器(Controller)和动态系统组成。

控制器会根据参考值(Reference)$r(t)$来决定控制量，即动态系统的输入$u(t)$。这种简单的控制方式称为开环(Open Loop)控制。当系统的全部信息可知且准确时，开环控制可以完美地达成控制目标。

如果希望精确地控制系统，则需要使用闭环(Closed Loop)控制系统，它与开环控制的最大区别是，在闭环控制中会测量系统的输出，并将其反馈(Feedback)到输入端与参考值进行比较考值与实际系统输出的差称为误差(Error),控制器将根据误差调整控制量。闭环控制系统可以实现高精度的控制，同时补偿由于外界扰动及系统建模不准确而引起的偏差。

2. 状态空间表达State-Space Representation

状态空间方程（State Space Model）描述系统数学模型的方法。状态空间方程式现代控制理论的基础，它以矩阵的形式表达系统状态变量、输入及输出之间的关系。可以描述和处理多输入输出（Multiole Input Multiple Output,MIMO）的系统。目前流行的一些算法，如模型预测控制、卡尔曼滤波器及最优控制，都是在状态空间方程的表达形式基础上发展而来的。

对于同样的系统，在现代控制理论中则会使用状态空间方程的表达状态空间方程是一个集合，它包含了系统的输入、输出及状态变量，并把它们用一系列的一阶微分方程表达出来。对于本例中的二阶系统，为了将其写成状态空间方程，需要选取合适的状态变量(State Variables),才能使二阶系统转化为一系列的一阶系统。

上述形式可推广并得到状态空间方程的一般形式，即：
$$\{\begin{array}{l}\frac{\mathrm{d}\mathbf{z}\left(t\right)}{\mathrm{d}t}=A\mathbf{z}\left(t\right)+B\mathbf{u}\left(t\right)\\ \mathbf{y}\left(t\right)=C\mathbf{z}\left(t\right)+D\mathbf{u}\left(t\right)\end{array}$$
其中：
$\mathbf{z}\left(t\right)$是状态变量，是一个$n$维向量：$\mathbf{z}\left(t\right)={\left[z_1\left(t\right),z_2\left(t\right),\cdots z_{\mathrm{n}}\left(t\right)\right]}^{\mathrm{T}}$
$\mathbf{y}\left(t\right)$是系统输出，是一个$m$维向量：$\mathbf{y}\left(t\right)={\left[y_1\left(t\right),y_2\left(t\right),\cdots y_{\mathrm{m}}\left(t\right)\right]}^{\mathrm{T}}$
$\mathbf{u}\left(t\right)$是系统输入，是一个$p$维向量：$\mathbf{u}\left(t\right)={\left[u_1\left(t\right),u_2\left(t\right),\cdots u_{\mathrm{p}}\left(t\right)\right]}^{\mathrm{T}}$

这说明，当使用状态空间方程来描述系统时，有$n$个状态变量、$m$个输出和$p$个输入。它可以表达多状态多输出、多输人的系统。其中，矩阵$A$是$n\times n$矩阵，表示系统状态变量之间的关系，称为状态矩阵或者系统矩阵。矩阵$B$是$n\times p$矩阵，表示输入对状态变量的影响，称为输入矩阵或者控制矩阵。矩阵$C$是$m\times n$矩阵，表示系统的输出与系统状态变量之间的关系，称为输出矩阵。矩阵$D$是$m\times p$矩阵，表示系统的输入直接作用在系统输出的部分，称为直接传递矩阵。

上述弹簧阻尼系统，因为它只有一个输入和一个输出，所以本系统属于单输入单输出(Single Input Single Output,SISO)系统。

多输入多输出(Multiple Inputs Multiple Outputs,MIMO)系统见CH06

2.1 状态空间方程与传递函数的关系

如果令$G(s)$的分母部分为零，即$|sI-A|=0$,得出的$s$值有两个含义：第一，从传递函数的角度考虑，它是传递函数的极点；第二，从状态矩阵的角度考虑，它是矩阵$A$的特征值(令$|sI-A|=0$是求矩阵$A$特征值的公式)。通过分析传递函数极点可以判断系统的表现。而当把系统写成状态空间方程之后，状态矩阵$A$的特征值即为其相对应的传递函数$G(s)$的极点。因此，通过分析矩阵$A$的特征值也可以判断系统的表现。

2.2 状态空间方程的解——矩阵指数函数

3. Phase Portrait相图，相轨迹

3 1. 1-D

这两个点被称为平衡点(Equilibrium Point或者Fixed Point)。

需要注意的是，只有当初始位置在$x_{f2}$左边，即$x(0)<x_{f2}$时，状态变量才可以回到平衡点。因此，$x_{f1}$是一个局部(Local)稳定的平衡点。

3 2. 2-D

图2中，相轨迹是一条曲线,但仍然是远离平衡点位置的。在这种情况下，平衡点称为不稳定节点(Unstable Node)
图3中，平衡点称为鞍点(Saddle)，是一个不稳定的点。

3 3. General Form

II 是以原点为中心的椭圆方程，这说明相图中的点沿椭圆的轨迹运行。在这种情况下，平衡点称为中心点(Center),相轨迹会围绕着这个中心点做圆周运动。判断相轨迹的运动方向，可以以一个在横轴的点进行分析尝试。发现$x_1$与$x_2$此消彼长，循环往复。如果从能量的角度来分析，它们的总能量取决于初始状态$x(0)$随着时间发生改变。所以这个系统在稳定与不稳定之间，$x(t)$始终有界但始终不为0。

会持续地振荡且振幅不断地加强。在这种情况下，平衡点称为不稳定焦点(Unstable Spiral)


可以判断出它的平衡点是一个稳定焦点(Stable Spiral)。相轨迹将沿螺旋线指向原点。其所对应的时间函数将振荡衰减，直至为0。

3 4. Summary

上述例子说明，状态矩阵$A$的特征值将决定平衡点的类型及系统的表现。通过上述分析可知，状态矩阵$A$的特征值实部部分决定了平衡点的稳定性，而特征值的虚部部分决定了系统是否会有振动。

3.5. 爱情中的数学-Phase Portrait 相图动态系统分析

动态系统的分析可以分为三个步骤：

1. 描述系统，即通过语言来描述系统的特性；
2. 数学分析，即使用数学工具对系统进行量化解析；
3. 结果与讨论，即根据第二步数学分析的结果，进行深层次的思考与讨论。
   
   
   

3.6 连续系统离散化

3.7 Summary

• 状态空间表达形式：
  用一系列的一阶微分方程表达系统的输入、输出及状态变量。其一般形式为
  $$\begin{gathered} \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}=Az\left(t\right)+Bu\left(t\right) \\ y\left(t\right)=Cz\left(t\right)+Du\left(t\right) \end{gathered}$$
  状态矩阵的特征值与其所对应的单输人单输出传递函数的极点相同。极点决定系统的表现，状态矩阵的特征值是研究的重点
• 相平面与相轨迹分析：
  利用矩阵特征值与特征向量的性质可以将矩阵对角化，从而将系统解耦。
  利用图形的方法，可以直观地分析复杂的非线性一阶系统平衡点的表现。
  二阶系统平衡点的性质由状态矩阵的特征值决定。
• 动态系统的分析方法：
  第一步，描述系统。通过语言来描述系统的特性。
  第二步，数学分析。使用数学工具对系统进行解析。
  第三步，结果与讨论。分析的结果，进行深层次的思考与讨论。

4. 系统的可控性Controllability(LTI)线性时不变

时不变性是指如果系统的输入喜好延迟了时间$T$, 那么系统的输出也会延迟时间$T$。一般情况下，时不变系统的数学表达式中都是常数系统（系数不是时间的函数）。线性时不变系统必须同时满足如下的两个性质。

需要说明的是，从严格意义上讲，时不变系统是不存在的，因为不能两次踏进同一条河流”,但在大部分工程情况下，在系统分析的时间区间内，参数是恒定的或者是缓慢变化的。对于非线性的系统，一般可以做线性化处理(参考附录A)。以近似为线性时不变的系统不在本书的讨论范围之内。

在设计控制器之前，需要判断一个先决条件，即系统的能控性(Controllability)。

4.1 系统的能控性的直观理解

换言之，我们能否通过控制作用在第一辆车上的外力同时控制两辆小车的位置和速度?这一问题需要在设计控制器之前解决。

4.2 系统的能控性的定义与判据

状态能控性定义：
对于系统$\dot{z}\left(t\right)=Az\left(t\right)+Bu\left(t\right)$而言，如果存在着输入$u(t)$,可以在有限的时间区间$\left[t_0,t_1\right]$（其中$t_1$有限） )内，将系统的状态变量从初始状态$z\left(t_0\right)$(其中转移到终端状态$z\left(t_1\right)$，那么就称状态$z\left(t_0\right)$是能控的状态。如果在任意的初始时间$t_0$下的初始状态$z\left(t_0\right)$都能控，就称系统的状态是能控的。需要指出，如果系统的状态$z(t)$能控，系统的输出$y(t)$也一定能控。

状态能控性判据：
对于n维线性时不变系统而言，它的状态能控的充分必要条件是能控矩阵 $C_0=\left[\begin{array}{lcccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right]$ 的秩为$n$，即$Rank\left(C_0\right)=n$。

有两点需要说明：

• 第一，能控择合适的输入，可以性是指理论上能控，但具体到实际问题中，要考虑系统的物理限制。例如在本例中，弹簧超过一定长度之后就会发生不可逆的形变。
• 第二，能控性表明系统的状态可以被控制到任意的终端状态，但是不代表系统可以稳定在任意的终端状态。

5. 稳定性stability-李雅普诺夫Lyapunov

CH01-2 从直观上解释了稳定性的含义，下面将介绍严谨的数学定义。在1892年，俄国数学家亚历山大·李雅普诺夫(Aleksandr Lyapunov)在其博士论文《运动稳定性的一般问题》中提出了稳定性的科学概念。本书将选用这个概念来定义系统的稳定性，它是一个通用的概念，既可以运用在线性系统中，也可以运用到非线性的系统分析中。

Stability in the sense of Lyapunov

渐近稳定性Asymptotic Stability——比李雅普诺夫意义下的稳定性更加严格的一种稳定

如果平衡点不符合上面两种条件，则不稳定。

在经典控制理论中，稳定特指渐近稳定。李雅普诺夫意义下的稳定(即极点在虚轴上的情况)会被称为临界稳定或者不稳定。在这样的定义下，从经典控制理论的角度来看，

参数$\delta (t_0)$和$\epsilon$的物理意义可以这样来理解：$\epsilon$是一个稳定性的指标，如果状态变量始终在$\epsilon$以内，那么平衡点就符合李雅普诺夫意义下的稳定。$\delta (t_0)$则是平衡点稳定的前提条件，或者说是稳定所能承受的最大干扰，也可以理解为收敛域。

根据上述分析，如果$\delta (t_0)$可以任意选择(选择无限大),那么就可以推断出平衡点是全局稳定(Global Stability),因为不管系统的初始状态在任何位置，它都可以最终收敛到一个范围之内(渐近稳定时收敛于0)。反之，如果$\delta (t_0)$的选择是有条件的，则平衡点是局部稳定(Local Stability)。

5.1 稳定性与状态空间方程

使用状态空间方程描述线性时不变系统的一般表达式为：
$$\begin{gathered} \frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}=Az\left(t\right)+Bu\left(t\right) \\ y\left(t\right)=Cz\left(t\right)+Du\left(t\right) \end{gathered}$$
其中，$z(t)$是状态变量，$y(t)$是系统的输出，$u(t)$是系统的输入，矩阵$A$是状态矩阵，矩阵$B$是输入矩阵，矩阵$C$是输出矩阵，矩阵$D$是直接传递矩阵。系统的输出$y(t)$是状态变量$z(t)$与输入$u(t)$的线性组合，如果系统的状态变量和输入都有界，那么系统的输出也是有界的(符合李雅普诺夫意义下的稳定性)。

首先考虑$0$输入状态，即$u(t)=0$。考虑状态矩阵$A$的特征值与平衡点类型之间的关系，如果$A$是一个二维矩阵，那么其特征值与稳定
性的关系如下所示：

上述分析方法可以推广到更高维度的状态矩阵中。对于$n$维向量$z(t)$,首先令$z(t)=P\bar{z}(t)$,其中，$P$是过渡矩阵，由矩阵$A$的特征向量组成。可得
$$\frac{\mathrm{d}\bar{z}(t)}{\mathrm{d}t}=\left[\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_{\mathrm{n}}\end{array}\right]\bar{z}(t)$$
其中${\lambda }_{\mathrm{i}}$表示A的特征值，$\{\begin{array}{l}{\bar{z}}_1(t)=C_1{e}^{{\lambda }_{1}t}\\ ⋮\\ {\bar{z}}_{\mathrm{n}}(t)=C_{\mathrm{n}}{e}^{{\lambda }_{\mathrm{n}}t}\end{array}$

原向量$z(t)$是$\bar{z}(t)$的线性组合，所以它的收敛或发散与$\bar{z}(t)$一致。此，我们可以将二维状态变量平衡点稳定判定方法沿用到更高维度的情况下，得到关于状态空间方程稳定性的两个结论（考虑零输入系统的状态空间方程为）：$\frac{\mathrm{d}z(t)}{\mathrm{d}t}=Az\left(t\right)$

• 如果$A$的特征值的实部都不大于0,它的平衡点将符合李雅普诺夫意义下的稳定性。
• 如果A的特征值的实部都小于0,它的平衡点将符合渐近稳定性。

上述结论为系统的控制器设计提供了思路。在闭环控制系统中，输入$u(t)$是状态变量的一个函数，例如$u(t)=-Kz(t)$,其中矩阵$K$是控制矩阵。
$$\frac{\mathrm{d}z(t)}{\mathrm{d}t}=Az\left(t\right)-BKz\left(t\right)=\left(A-BK\right)z\left(t\right)=A_{\mathrm{cl}}z\left(t\right)$$
其中，$A_{cl}=A-BK$,代表闭环控制系统的状态矩阵。根据上述分析，如果希望得到一个渐近稳定的系统，则需要设计合适的控制矩阵$K$,使得$A_{cl}$的特征值实部都为负数。

5.2 Summary

• 稳定性的定义：
  李雅普诺夫意义下的稳定性：随着时间的增加，系统的状态变量始终在平衡点附近移动(有界)。
  渐近稳定性：随着时间的增加，系统的状态变量会最终收敛于平衡点。
• 稳定性与传递函数：
  在研究系统稳定性的时候考虑单位冲激响应，即传递函数本身。
  系统稳定的条件是系统的闭环传递函数的极点均在复平面的左半部分(实部小于0)。此时系统满足有界输入有界输出稳定。
• 稳定性与状态空间方程： 状态矩阵的特征值的实部决定了系统的稳定性：
  当实部都不大于0时，系统符合李雅普诺夫意义下的稳定性。
  当实部都小于0时，系统符合渐近稳定性。

6. 线性控制器设计Linear Controller Design

本章将从状态空间方程的角度设计控制器，从一个案例入手，深入地讨论状态反馈控制器的设计思路和方法，包含极点配置、最优化控制、轨迹追踪以及线性观测器的设计与应用。

本章的学习目标为：
掌握系统能控性的概念和判断系统能控性的方法。
掌握线性状态反馈控制器的设计思路与设计流程。
了解最优化控制器的设计思路与目标。
掌握轨迹追踪控制器的设计思路与设计流程。
掌握系统能观测性的概念和判断系统能观测性的方法。
掌握线性观测器的设计思路与方法。
掌握线性观测器和控制器结合设计的思路与方

6.1 引子——指尖上的平衡

6.1.1 PID控制方案

闭环传递函数的极点随着K的增加将沿着实轴相向移动，在虚轴汇合后指向无穷，成为两个共轭的纯虚数。这意味着无论增益K如何增大，都无法使系统稳定。因此，若为保障系统稳定，则需要在复平面虚轴左边增加零点，使得根轨迹的渐近线向左边移动。同时，系统也需要增加极点以消除系统的稳态误差，因此可以使用PID控制器。

传递函数$G(s)$本身含有一个正数极点$\sqrt{g/d}$,这就决定了无论如何去增加极点/零点，闭环传递函数的根轨迹总会有一条分支从$s_{p1}$出发向着零点或者无穷移动。这意味着需要足够大的增益$K$才能使其移动到复平面的左半部分，而过高的增益：带来强烈的振荡和过高的超调量。并且当增益过大的时候，系统的控制量$u(t)$也会变得很大，造成不必要的能量损耗。

上述问题体现了PID控制器的局限性，控制量$U(s)$是误差$E(s)$的函数，而误差$E(s)=Y(s)-R(s)$, 这说明在设计控制器时只考虑了系统的输出$Y(s)$,虽然足够简单，但是并没有提供全部的系统状态信息，因此灵活性不够。

6.1.2 状态空间方程建模

6.2 线性状态反馈控制器

在掌握系统能控性之后，本节将讨论线性状态反馈控制器(Linear State-FeedbackControl Design)。

• 极点配置

继续分析指尖平衡的例子：





从本质上来说，这依然是比例控制，但相较于传统方法(只反馈位移信息),所有的状态信息(包括位移和速度)都被用作反馈，因此有两个比例增益$k_1$和$k_2$。曾经介绍过状态矩阵的特征值对应于传递函数的极点，所以这种设计思路也被称为极点配置(PolePlacement)。

使用了全状态的反馈信息。设计核心是通过设计矩阵K使得闭环状态矩阵的特征值的实部部分都为负数。

7. 最优化控制初探——LQR控制器 Linear Quadratic Regulator

在设计反馈控制K的时候，如何选择闭环状态矩阵的特征值涉及最优化控制，从这点入手可以发展出一整个单独的学科和研究领域。——线性二次型调节器

最优化是当前最热门的领域之一，有很多新的算法被引入进来。但无论是机器学习、神经网络，还是其他的智能算法，其本质都是建立代价函数，设定不同的权重系数并求其极值(极大值或者极小值)。

上例中，可以说组1是最优的，因为它迅速地将连杆恢复到了平衡的位置。也可以说组3是最优的，因为它的总输入最小，意味着它的能耗最小。从性能的角度看，组1是最好的。从节能的角度看，组3则是最佳。作为最优化算法工程师，根据不同的应用场景去权衡(Tradeoff)权重系数，是非常重要的工作。

线性控制器设计-轨迹跟踪（Fellow a Desired Path）

此时我们思考另一个问题，如果系统中的某些状态变量无法测量例如在上述的例子中，没有办法实时得到连杆的角速度，那么状态反馈控制器也就无法使用了。若要解)决这个问题，需要用到观测器来实时估计系统的状态变量值。

8. 状态观测器设计 Linear Observer Design

如果系统的某些状态变量不可测，如何通过可测量的输出值估计状态值是很值得研究的问题。在很多情况下，传感器无法安装在我们需要测量的地方。例如，电动汽车电池内芯的温度就只能通过其表面温度估再如在隧道中运行的车辆，其速度很难直接测量，但可以根据其他信息估计。

比如我们现在注意到导航软件可以提示红绿灯的时间，实际上导航软件并没有连接交通网络中的红绿灯数据，因为红绿灯在最初设计和建造时根本没留这样的接口。

与控制器设计类似，在设计观测器之前，首先要明确状态是否可以通过输出观测到

8.1 系统的能观测性

对于线性时不变系统：

• 状态能观测性的定义：
  在任意给定的输入$u(t)$下，根据有限的时间区间$[t_0,t_1]$(其中$t_1$有限)的输入$u(t)$和输出值$y(t)$,可以唯一确定在初始时间$t_0$下的初始状态$z(t_0)$,则称系统在$t_0$时刻是能观测的，如果在任意初始时间$t_0$下的初始状态$z(t_0)$都能观测，就称系统的状态是能观测的。

• 状态能观测性判据：
  对于n维线性时不变系统而言，它的状态能观测的充分必要条件是能观测矩阵
  $$O={\left[\begin{array}{lcccc}C& CA& C{A}^2& \cdots & C{A}^{n-1}\end{array}\right]}^{\mathrm{T}}$$
  的秩为$n$，即$\mathrm{Rank}\left(O\right)=n$

8.2 线性观察器设计

。它相当于在“后台”同步运行另一套动态系统，而这个动态系统可以根据系统的输入$u(t)$和输出$y(t)$估计系统的状态值$z(t)$。

8.3 线性观察器举例

$l_1=1.5,l_2=-0.75$

9. 可观测性与分离原理——观测器与控制器的结合

需要特别注意的是，在选取$(A-LC)$和$(A-BK)$的特征值时，观测器的收敛速度应该快于控制器的收敛速度(一般要求快2～5倍)。因为只有这样才能保证控制器的设计是基于一个相对准确的估计值之上的。

10. 现代控制理论串讲

Summary

• 系统的能控性：
  系统能控的充分必要条件：能控矩阵$C_{\mathrm{o}}=\left[\begin{array}{lcccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right]$的秩为$n$
  系统能控不代表可以改变其平衡点或者令其状态变量按照一定轨迹移动
• 线性状态反馈控制器：
  线性反馈控制器的设计思路为极点配置。
  $u(t)=-Kz(t)$，设计$K$使得闭环状态矩阵$(A-BK)$的特征值实部都为负数。
  可以通过调整权重实现最优化控制
  $u\left(t\right)=F{z}_{\mathrm{d}}+K_{\mathrm{e}}e\left(t\right)$可以改变系统的平衡点
• 观测器设计:
  系统能观测的充分必要条件：能观测矩阵$O={\left[\begin{array}{lcccc}C& CA& C{A}^2& \cdots & C{A}^{n-1}\end{array}\right]}^{\mathrm{T}}$的秩为$n$
  线性观测器：$\dot{\hat{z}}=\left(A-LC\right)\hat{z}+\left(B-LD\right)u\left(t\right)+Ly\left(t\right)$，设计$L$使得$(A-LC)$的特征值实部都为负数。
  当控制器与观测器结合的时候，观测器的收敛速度要快于控制器

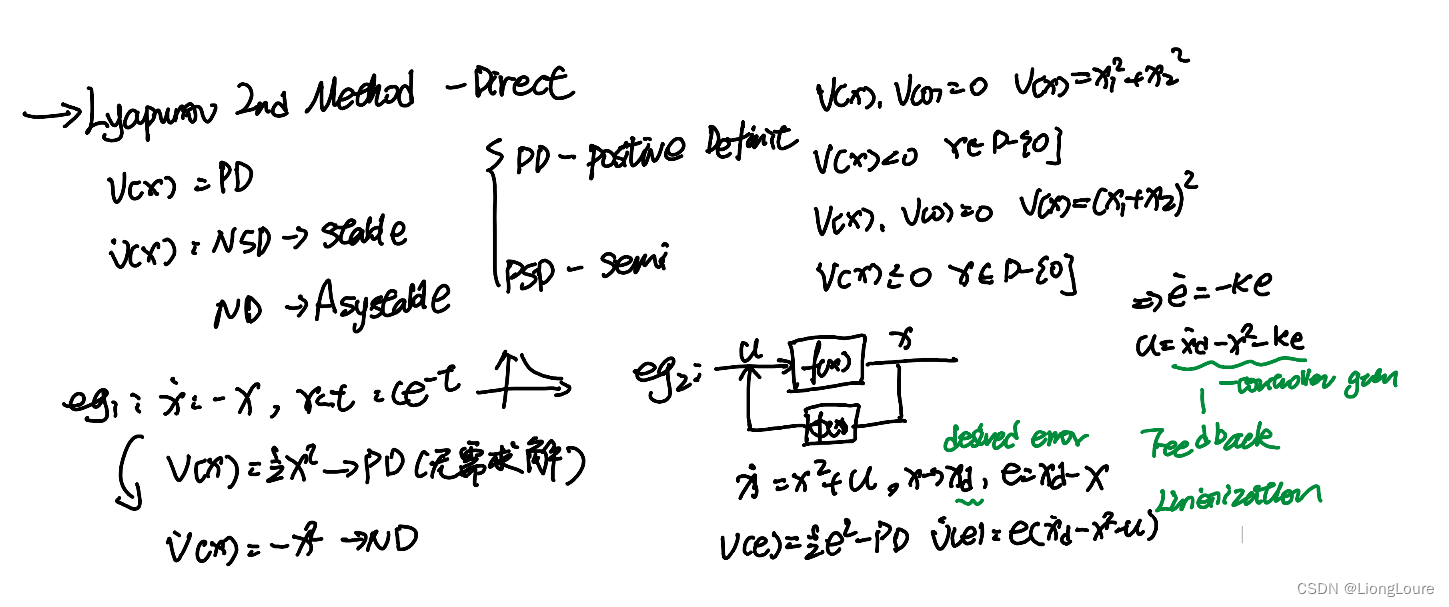
11. 非线性控制理论基础 Lyapunov直接方法

12. Invariance Princilpe-LaSalle;s Theorem不变性原理

13. Nonlinear Basic Feedback Stabilization 非线性系统稳定设计

14. Nonlinear Backstepping Control反馈线性化控制

Nonlinear Backstepping Controller 补充习题 - Backsteeping controller Design Review

15. NonlinearAdaptive Controller非线性自适应控制器

16. Robust Controller非线性鲁棒控制器

Robust Control : tp achieve robust performance and/or stability in percence of bounded modeling error

16.1 Slide Control 滑膜控制

16.2 High Gain + High Frequency

16.3 三种鲁棒控制器的比较+如何分析控制器

17. 三种鲁棒控制器的比较+如何分析控制器