目录
1. 2D-2D对级几何
对极约束简洁地给出了两个匹配点的空间位置关系。其推导过程为
两个匹配的特征点的归一化坐标
x
1
,
x
2
x_1,x_2
x1,x2之间的关系为:
x
2
=
R
x
1
+
t
\boldsymbol{x}_{2}=\boldsymbol{R} \boldsymbol{x}_{1}+\boldsymbol{t}
x2=Rx1+t
两边同时左乘 t^。回忆 ^ 的定义,这相当于两侧同时与 t 做外积:
t
∧
x
2
=
t
∧
R
x
1
\boldsymbol{t}^{\wedge} \boldsymbol{x}_{2}=\boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}_{1}
t∧x2=t∧Rx1
然后,两侧同时左乘
x
2
T
x^T_2
x2T :
x
2
T
t
∧
x
2
=
x
2
T
t
∧
R
x
1
=
0
\boldsymbol{x}_{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{x}_{2}=\boldsymbol{x}_{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}_{1}=0
x2Tt∧x2=x2Tt∧Rx1=0
1.1. 本质矩阵E
定义:
归一化平面上的匹配点之间的关系。
性质:
- 本质矩阵满足对极约束;
- 其奇异值必定为 [ σ , σ , 0 ] T [\sigma, \sigma,0]^T [σ,σ,0]T的形式;
- 自由度为5,最少可以用5对点求得,一般用8对点,也就是常说的8点法。
八点法求解本质矩阵
( u 1 , v 1 , 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) ( u 2 v 2 1 ) = 0 \left(u_{1}, v_{1}, 1\right)\left(\begin{array}{lll}{e_{1}} & {e_{2}} & {e_{3}} \\ {e_{4}} & {e_{5}} & {e_{6}} \\ {e_{7}} & {e_{8}} & {e_{9}}\end{array}\right)\left(\begin{array}{c}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=0 (u1,v1,1)⎝⎛e1e4e7e2e5e8e3e6e9⎠⎞⎝⎛u2v21⎠⎞=0
( u 1 1 u 2 1 u 1 1 v 2 1 u 1 1 v 1 1 u 2 1 v 1 1 v 2 1 v 1 1 u 2 1 v 2 1 1 u 1 2 u 2 2 u 1 2 v 2 2 u 1 2 v 1 2 u 2 1 v 1 1 v 2 1 v 1 2 u 2 2 v 2 2 1 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ u 1 8 u 2 8 u 1 8 v 2 8 u 1 8 v 1 8 u 2 8 v 1 8 v 2 8 v 1 8 u 2 8 v 2 8 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) = 0 \left(\begin{array}{cccccccc}{u_{1}^{1} u_{2}^{1}} & {u_{1}^{1} v_{2}^{1}} & {u_{1}^{1}} & {v_{1}^{1} u_{2}^{1}} & {v_{1}^{1} v_{2}^{1}} & {v_{1}^{1}} & {u_{2}^{1}} & {v_{2}^{1}} & {1} \\ {u_{1}^{2} u_{2}^{2}} & {u_{1}^{2} v_{2}^{2}} & {u_{1}^{2}} & {v_{1}^{2} u_{2}^{1}} & {v_{1}^{1} v_{2}^{1}} & {v_{1}^{2}} & {u_{2}^{2}} & {v_{2}^{2}} & {1} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} & {} \\ {u_{1}^{8} u_{2}^{8}} & {u_{1}^{8} v_{2}^{8}} & {u_{1}^{8}} & {v_{1}^{8} u_{2}^{8}} & {v_{1}^{8} v_{2}^{8}} & {v_{1}^{8}} & {u_{2}^{8}} & {v_{2}^{8}} & {1}\end{array}\right)\left(\begin{array}{c}{e_{1}} \\{e_{2}} \\{e_{3}} \\{e_{4}} \\ {e_{5}} \\ {e_{6}} \\ {e_{7}} \\ {e_{8}} \\ {e_{9}}\end{array}\right)=0 ⎝⎜⎜⎜⎛u11u21u12u22⋮u18u28u11v21u12v22⋮u18v28u11u12⋮u18v11u21v12u21⋮v18u28v11v21v11v21⋮v18v28v11v12⋮v18u21u22⋮u28v21v22v28111⎠⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛e1e2e3e4e5e6e7e8e9⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=0
最后解齐次方程可以通过SVD,或者算广义逆矩阵来计算,或者超定方程构建一个最小二乘式子来优化得到
1.2. 基础矩阵F
1.3. 单应矩阵H
理论上可以通过4对点算出(注意不能共线),但是orbslam2里用的是8对点。
n
T
P
+
d
=
0
−
n
T
P
d
=
1
p
2
=
K
(
R
P
+
t
)
=
K
(
R
P
+
t
⋅
(
−
n
T
P
d
)
)
=
K
(
R
−
t
n
T
d
)
P
=
K
(
R
−
t
n
T
d
)
K
−
1
p
1
\boldsymbol{n}^{T} \boldsymbol{P}+d=0\\ -\frac{\boldsymbol{n}^{T} \boldsymbol{P}}{d}=1\\ \begin{aligned} \boldsymbol{p}_{2} &=\boldsymbol{K}(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t}) \\ &=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t} \cdot\left(-\frac{\boldsymbol{n}^{T} \boldsymbol{P}}{d}\right)\right) \\ &=\boldsymbol{K}\left(\boldsymbol{R}-\frac{t \boldsymbol{n}^{T}}{d}\right) \boldsymbol{P} \\ &=\boldsymbol{K}\left(\boldsymbol{R}-\frac{t \boldsymbol{n}^{T}}{d}\right) \boldsymbol{K}^{-1} \boldsymbol{p}_{1} \end{aligned}
nTP+d=0−dnTP=1p2=K(RP+t)=K(RP+t⋅(−dnTP))=K(R−dtnT)P=K(R−dtnT)K−1p1
(
u
2
v
2
1
)
=
(
h
1
h
2
h
3
h
4
h
5
h
6
h
7
h
8
h
9
)
(
u
1
v
1
1
)
u
2
=
h
1
u
1
+
h
2
v
1
+
h
3
h
7
u
1
+
h
8
v
1
+
h
9
v
2
=
h
4
u
1
+
h
5
v
1
+
h
6
h
7
u
1
+
h
8
v
1
+
h
9
h
1
u
1
+
h
2
v
1
+
h
3
−
h
7
u
1
u
2
−
h
8
v
1
u
2
=
u
2
h
4
u
1
+
h
5
v
1
+
h
6
−
h
7
u
1
v
2
−
h
8
v
1
v
2
=
v
2
\left(\begin{array}{l}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=\left(\begin{array}{lll}{h_{1}} & {h_{2}} & {h_{3}} \\ {h_{4}} & {h_{5}} & {h_{6}} \\ {h_{7}} & {h_{8}} & {h_{9}}\end{array}\right)\left(\begin{array}{l}{u_{1}} \\ {v_{1}} \\ {1}\end{array}\right)\\ \begin{aligned} u_{2} &=\frac{h_{1} u_{1}+h_{2} v_{1}+h_{3}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \\ v_{2} &=\frac{h_{4} u_{1}+h_{5} v_{1}+h_{6}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \end{aligned} \\ \begin{array}{l}{h_{1} u_{1}+h_{2} v_{1}+h_{3}-h_{7} u_{1} u_{2}-h_{8} v_{1} u_{2}=u_{2}} \\ {h_{4} u_{1}+h_{5} v_{1}+h_{6}-h_{7} u_{1} v_{2}-h_{8} v_{1} v_{2}=v_{2}}\end{array}
⎝⎛u2v21⎠⎞=⎝⎛h1h4h7h2h5h8h3h6h9⎠⎞⎝⎛u1v11⎠⎞u2v2=h7u1+h8v1+h9h1u1+h2v1+h3=h7u1+h8v1+h9h4u1+h5v1+h6h1u1+h2v1+h3−h7u1u2−h8v1u2=u2h4u1+h5v1+h6−h7u1v2−h8v1v2=v2
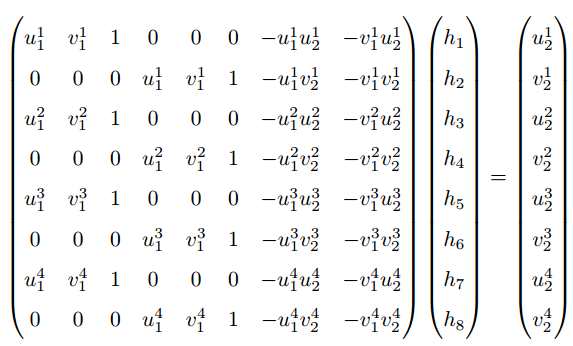
通过奇异值分解(SVD)求解透视变换单应性矩阵
2. 3D-2D:pnp
2.1.DLT
每对点提供2项约束,理论上6对点即可算出。
[ R | t ]一共有12维矩阵,本来有6个自由度,在计算的时候忽略其内在的约束。所以需要6对点;
最后解齐次方程可以通过SVD,或者算广义逆矩阵来计算,或者超定方程构建一个最小二乘式子来优化得到
[PnP] PnP问题之DLT解法
2.2.epnp
每对点提供2项约束,理论上6对点即可算出。
[PnP]PnP问题之EPnP解法
2.3. p3p
只能使用3对点。实际需要4对点,其中一对点用于验证。
相机位姿求解——P3P问题
2.4. BA
3. 3D-3D
3.1. ICP-SVD
[LIDAR-SLAM] Iterative Closest Point (ICP)简单实现
3.1. ICP-BA(非线性优化)
3.2.sim3
只需3对点
ORB-SLAM2代码阅读笔记(十):sim3求解
特征
线特征
LSD,LBD
利用Canny边缘检测算子进行边缘检测的原理及OpenCV代码实现
经典霍夫变换(Hough Transform)
点特征
SIFT算法详解
Sift算子特征点提取、描述及匹配全流程解析
surf算法原理-包你明白surf过程
SURF到底比SIFT快在哪里?
Harris角点算法
ORB






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








