slam14讲（第7讲、前端里程计）计算相机运动

计算相机运动

计算相机运动的前提是有了匹配好的点对，这个可以通过slam14讲前面所介绍的，提取orb特征点和描述子，做特征匹配来得到（比较耗时），也可以通过后面介绍的光流法来得到匹配好的点对。计算相机运动的方法主要如下：

1. 2D-2D的求解，通常是用对极几何来求解，用于单目的场合中。
2. 3D-3D的求解，这时候就可以像点云一样去做icp求解，用于深度相机、双目的场合
3. 3D-2D的求解，就是已知一组3D点和一组2D点，通过pnp求解，用于深度相机，双目或者激光雷达相机融合的场合。

2D-2D，对极几何

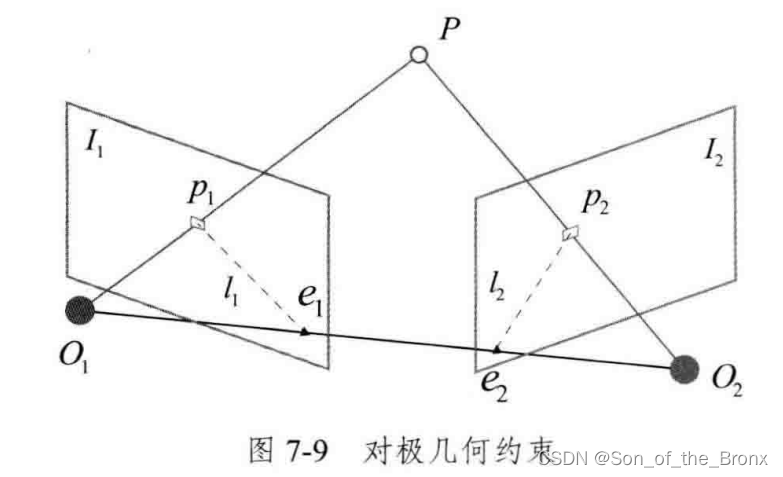
这个是两帧成像平面的示意图，求的就是第一帧到第二帧的变换关系R和t。对于这个图，只要理解到$O_1$、$O_2$、$P$确定了一个极平面，$p_2和e_2$构成极线$l_2$其实就是3D点$P$可能出现在第二帧图像的位置，但是通过对应点匹配的操作，可以直接确定到具体的像素上。说人话就是：现在已知两组2D点还有他们的对应关系，通过构建方程来求解第一帧到第二帧的变换关系R和t。

问题的构建

设P在第一帧相机坐标系下的3D位置是：
$\mathbf{P}=[X,Y,Z{]}^{\mathrm{T}}$

---

两帧图像的投影：
${\mathbf{p}}_1\simeq \mathbf{KP},{\mathbf{p}}_2\simeq \mathbf{K}(\mathbf{RP}+\mathbf{t})$

---

${\mathbf{x}}_1、{\mathbf{x}}_2$是归一化平面上的坐标，就是X、Y除以深度Z的坐标：
${\mathbf{x}}_1=[X/Z,Y/Z,1]$

---

变量转移后得到：
${\mathbf{x}}_1={\mathbf{K}}^{-1}{\mathbf{p}}_1,{\mathbf{x}}_2={\mathbf{K}}^{-1}{\mathbf{p}}_2$

---

${\mathbf{x}}_1、{\mathbf{x}}_2$的关系就是由代求的变换关系R和t来组成：
${\mathbf{x}}_2\simeq \mathbf{R}{\mathbf{x}}_1+\mathbf{t}$

---

接下来就是两边同时左乘$t^{\wedge }$，去消除变量$t$，得到下式：
${\mathbf{t}}^{\wedge }{\mathbf{x}}_2\simeq {\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$

---

再同时左乘$x_2^T$，得到：
${\mathbf{x}}_2^{\mathrm{T}}{\mathbf{t}}^{\wedge }{\mathbf{x}}_2\simeq {\mathbf{x}}_2^{\mathrm{T}}{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$.

---

左部分很明显是为0的，因为${\mathbf{t}}^{\wedge }{\mathbf{x}}_2$叉乘的向量与$t和x_2$都是垂直的，所以内积一定为0。最终得到下式，都叫对级约束：
${\mathbf{x}}_2^{\mathrm{T}}{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1=0$.
${\mathbf{p}}_2^{\mathrm{T}}{\mathbf{K}}^{-\mathrm{T}}{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1=0$.
对于这两个最终的式子，书上给了定义是基础矩阵F和本质矩阵E：
$\mathbf{E}={\mathbf{t}}^{\wedge }\mathbf{R}$
$\mathbf{F}={\mathbf{K}}^{-\mathrm{T}}\mathbf{E}{\mathbf{K}}^{-1}$

---

主要的求解流程：

1. 根据匹配点对求出E
2. 根据E恢复出R和t。

求解本质矩阵

对于本质矩阵E来说，有以下特性：

1. 因为最终关于本质矩阵的对级约束等式是为0的，所以乘任何非0的数，等式是成立的，所以本质矩阵E有尺度等价性。
2. 本质矩阵E的奇异值必定是$[\sigma ,\sigma ,0{]}^{\mathrm{T}}$，这个是本质矩阵的内在属性。
3. 虽然说E是由R和t组成，应该有6个自由度，但是因为尺度等价性，所以E实际只有5个自由度。
   E虽然是5个自由度，但是旋转内在的非线性性质，所以求解的时候只考虑尺度等价性，采用8点法来估计E。

只考虑一对匹配点，他们的归一化坐标是${\mathbf{x}}_1={\left[u_1,v_1,1\right]}^{\mathrm{T}},{\mathbf{x}}_2={\left[u_2,v_2,1\right]}^{\mathrm{T}}$，根据对极约束：
$\left(u_2,v_2,1\right)\left(\begin{array}{lll}{e}_1& e_2& e_3\\ e_4& e_5& e_6\\ e_7& e_8& e_9\end{array}\right)\left(\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right)=0$
然后将E展开：
$\mathbf{e}={\left[e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9\right]}^{\mathrm{T}}$
对极几何约束写成与$\mathbf{e}$有关的线性形式：
$\left[u_2{u}_1,u_2{v}_1,u_2,v_2{u}_1,v_2{v}_1,v_2,u_1,v_1,1\right]\cdot \mathbf{e}=0$
然后将其他匹配点对放到一个方程中，变成一个线性方程组：
$\left(\begin{array}{ccccccccc}{u}_2^1{u}_1^1& u_2^1{v}_1^1& u_2^1& v_2^1{u}_1^1& v_2^1{v}_1^1& v_2^1& u_1^1& v_1^1& 1\\ u_2^2{u}_1^2& u_2^2{v}_1^2& u_2^2& v_2^2{u}_1^2& v_2^2{v}_1^2& v_2^2& u_1^2& v_1^2& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \\ u_2^8{u}_1^8& u_2^8{v}_1^8& u_2^8& v_2^8{u}_1^8& v_2^8{v}_1^8& v_2^8& u_1^8& v_1^8& 1\end{array}\right)\left(\begin{array}{c}{e}_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6\\ e_7\\ e_8\\ e_9\end{array}\right)=0$

系数矩阵的大小是8*9，如果系数矩阵是满秩（秩为8），零空间维数为1，也就是$\mathbf{e}$构成直线，与$\mathbf{e}$尺度等价性是一致的。

从本质矩阵恢复R和t

求解出E后，通过奇异值求解(SVD)恢复出相机的R和t。设E的SVD为：
$\mathbf{E}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$
$\mathbf{U}和\mathbf{V}$是正交阵，$\mathbf{\Sigma }$是奇异值矩阵。在奇异值分解中，对任意一个E，存在两种可能的R和t对应：
$\begin{array}{rl}{\mathbf{t}}_1^{\wedge }& =\mathbf{U}{\mathbf{R}}_Z\left(\frac{\pi }{2}\right)\mathbf{\Sigma }{\mathbf{U}}^{\mathrm{T}},{\mathbf{R}}_1=\mathbf{U}{\mathbf{R}}_Z^{\mathrm{T}}\left(\frac{\pi }{2}\right){\mathbf{V}}^{\mathrm{T}}\\ {\mathbf{t}}_2^{\wedge }& =\mathbf{U}{\mathbf{R}}_Z\left(-\frac{\pi }{2}\right)\mathbf{\Sigma }{\mathbf{U}}^{\mathrm{T}},{\mathbf{R}}_2=\mathbf{U}{\mathbf{R}}_Z^{\mathrm{T}}\left(-\frac{\pi }{2}\right){\mathbf{V}}^{\mathrm{T}}.\end{array}$
又因为-E和E等价，所以对任意一个t取负号，也可以得到相同结果。所以从E分解得到的R和t一共有4个可能的解。只需要将任意一个点带入4中解中，检测这个点在两个相机下的深度，就可以确定哪一个解是正确的。

三角测量

因为单目slam中，通过单张图像没法获取像素的深度，所以需要三角测量来估计像素的深度。

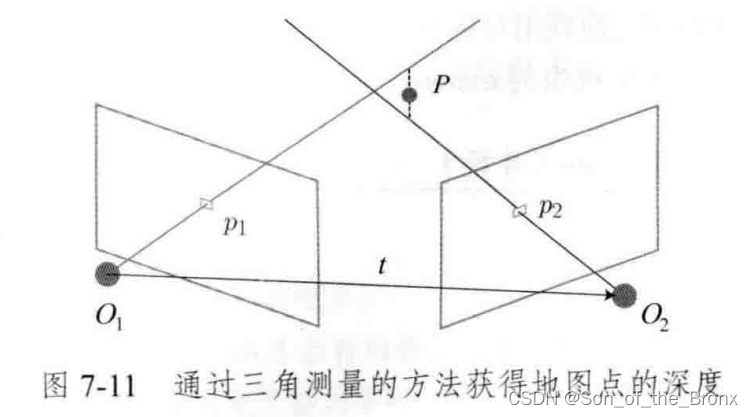
三角测量应该是在对极几何之后的操作，这个是已知两帧图像的R和t，求这两个特征点的深度。根据对极几何的定义，${\mathbf{x}}_1、{\mathbf{x}}_2$是两个特征点归一化坐标。满足下面式子：
$s_2{\mathbf{x}}_2=s_1\mathbf{R}{\mathbf{x}}_1+\mathbf{t}$
然后左乘${\mathbf{x}}_2^{\wedge }$，得到下面式子：
$s_2{\mathbf{x}}_2^{\wedge }{\mathbf{x}}_2=0=s_1{\mathbf{x}}_2^{\wedge }\mathbf{R}{\mathbf{x}}_1+{\mathbf{x}}_2^{\wedge }\mathbf{t}$.
也是求解一个方程。得到$s_1$后$s_2$也可以得出。
三角化也可以像orbslam那样处理，ORB-SLAM2之单目特征点对三角化。

3D-2D，PnP

PnP是求3D到2D点对运动的方法。如果两张图象中一张特征点的3D位置已知，最少只需要3个点对（以及至少一个额外点验证结果）即可估计相机运动。
PnP的解法有很多：

1. P3P（3对点估计位姿）
2. 直接线性变换（DLT）
3. 最小化重投影误差BA

直接线性变换（DLT）

考虑第一帧图像的空间点$P$，齐次坐标为$P=(X,Y,Z,1)$，在第二帧图像中对应的投影点是$x_2=(u_2,v_2,1)$，这个是归一化平面的点，不是图像的像素（ps：这里我跟书上的定义不一样，因为我认为第一帧图像中的点才是$x_1$，第二帧才是$x_2$）。
可以通过R和t构建两帧图像的信息：（3×4的矩阵包含两帧图像的旋转和平移，s是第二帧点的深度）
$s\left(\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right)=\left(\begin{array}{cccc}{t}_1& t_2& t_3& t_4\\ t_5& t_6& t_7& t_8\\ t_9& t_{10}& t_{11}& t_{12}\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)$

用最后一行把s消去得到两个约束：
$u_2=\frac{t_{1}X+t_{2}Y+t_{3}Z+t_4}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}},v_2=\frac{t_{5}X+t_{6}Y+t_{7}Z+t_8}{t_{9}X+t_{10}Y+t_{11}Z+t_{12}}$

---

然后通过定义行向量来简化表示：
${\mathbf{t}}_1={\left(t_1,t_2,t_3,t_4\right)}^{\mathrm{T}},{\mathbf{t}}_2={\left(t_5,t_6,t_7,t_8\right)}^{\mathrm{T}},{\mathbf{t}}_3={\left(t_9,t_{10},t_{11},t_{12}\right)}^{\mathrm{T}}$,
最后有：
$\begin{array}{rl}& {\mathbf{t}}_1^{\mathrm{T}}\mathbf{P}-{\mathbf{t}}_3^{\mathrm{T}}\mathbf{P}{u}_2=0,\\ & {\mathbf{t}}_2^{\mathrm{T}}\mathbf{P}-{\mathbf{t}}_3^{\mathrm{T}}\mathbf{P}{v}_2=0.\end{array}$

---

每个特征点对提供两个约束方程。如果有N个特征点，则有下面的方程组：

$\left(\begin{array}{ccc}{\mathbf{P}}_1^{\mathrm{T}}& 0& -u_1{\mathbf{P}}_1^{\mathrm{T}}\\ 0& {\mathbf{P}}_1^{\mathrm{T}}& -v_1{\mathbf{P}}_1^{\mathrm{T}}\\ ⋮& ⋮& ⋮\\ {\mathbf{P}}_N^{\mathrm{T}}& 0& -u_N{\mathbf{P}}_N^{\mathrm{T}}\\ 0& {\mathbf{P}}_N^{\mathrm{T}}& -v_N{\mathbf{P}}_N^{\mathrm{T}}\end{array}\right)\left(\begin{array}{l}{\mathbf{t}}_1\\ {\mathbf{t}}_2\\ {\mathbf{t}}_3\end{array}\right)=0$.

这个3×4的矩阵一共12维，而因为每个特征点对都有2个约束，所以至少通过6个匹配点对实现R和t的求解。如果特征点对大于6对，则可通过最小二乘来求解。

P3P

我这里做一个大概的讲解，因为书上也不是很详细。也可以参考参考这篇文章。PnP问题之P3P求解方式。
我们首先需要知道的是P3P并不是直接根据2D-3D点求出相机位姿矩阵，而是先求出对应的2D点在当前相机坐标系下的3D坐标，然后根据世界坐标系下的3D坐标和当前相机坐标系下的3D坐标通过ICP信息求解相机位姿的。

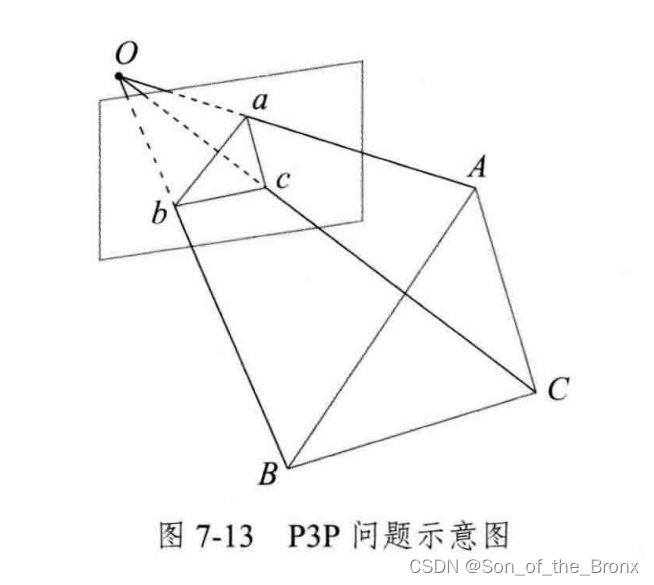
求解过程

1. 已知这三个点A、B、C在世界坐标系下的坐标
2. 已知AB、BC、AC的距离信息，还有对应的角度信息（这个可以从图像中得知，因为是相似的）
3. 根据解方程组 ，计算出OA、OB、OC的距离，再引入一个验证点计算最可能的解，进而求出A、B、C在相机坐标系下的坐标
4. 最后就是简单的已知匹配关系的ICP匹配，求解出相机与世界的相对位姿。

缺点

1. P3P只利用了三个点信息，有更多点的时候没法运用
2. 如果3D点或者2D点受噪声影响，可能会导致算法失效。

最小化重投影误差BA

直接就是看图说话吧，我还是感觉14讲里讲的有点啰嗦，而且下标不太清晰。

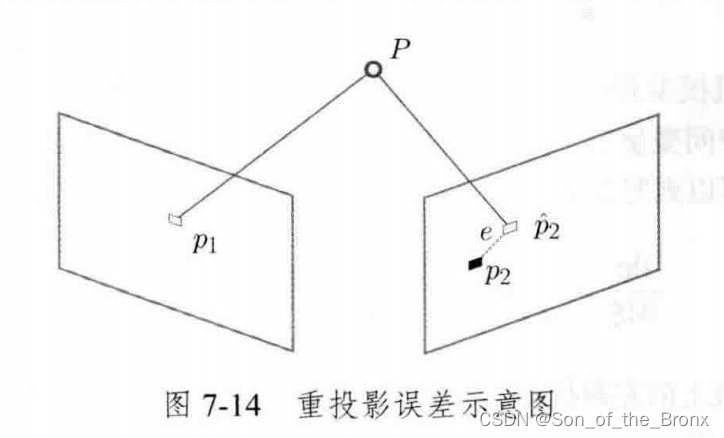
已知条件：第一帧图像中知道了点$P_{c_1}$（空间点$P$在第一帧相机坐标系的3D位置），已知第二帧图像中的对应点$p_2$，这个${\hat{p}}_2$是指通过R和t投影到第二帧的像素坐标，如下式（忽略了齐次坐标的转换）：
${\hat{p}}_2=\frac{1}{z_{c_2}}K\ast T\ast P_{c_1}$

---

这时${\hat{p}}_2$是根据估计的R和t投影到第二帧图像的像素，与$p_2$这个通过特征点匹配得到的像素有误差，有误差就可以通过求解一个最小投影误差的方法去求解一个较优的位姿。误差e为：
$e=p_2-\frac{1}{z_{c_2}}K\ast T\ast P_{c_1}$

---

${\mathbf{T}}^{\ast }=\arg {\min }_{\mathbf{T}}\frac{1}{2}{\sum }_{i=1}^n{\Vert {\mathbf{u}}_i-\frac{1}{s_i}\mathbf{K}\mathbf{T}{\mathbf{P}}_i\Vert }_2^2$.
上面是书上的目标函数，本质上是一样的，只是我把它讲成第一帧第二帧图像好理解。
对于这个目标函数，首先就是线性化：
$\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})\approx \mathbf{e}(\mathbf{x})+{\mathbf{J}}^{\mathrm{T}}\Delta \mathbf{x}$.

---

这个雅可比矩阵直接就是用se(3)上李代数求导的结论。
$\frac{\partial \mathbf{e}}{\partial \delta \mathbf{\xi }}=-\left[\begin{array}{cccccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}& -\frac{f_x{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& f_x+\frac{f_x{X}^{\prime 2}}{Z^{\prime 2}}& -\frac{f_x{Y}^{\prime }}{Z^{\prime }}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_y{Y}^{\prime }}{Z^{\prime 2}}& -f_y-\frac{f_y{Y}^{\prime 2}}{Z^{\prime 2}}& \frac{f_y{X}^{\prime }{Y}^{\prime }}{Z^{\prime 2}}& \frac{f_y{X}^{\prime }}{Z^{\prime }}\end{array}\right]$
就是一个2×6的矩阵，也符合常识，图像像素的两个观察量（行列）来更新这个六维自由的变换矩阵。最后就是高斯牛顿来解这个最小二乘问题。

总结

这个Bundle Adjustment是用的非常多的算法，只要有3D点和2D点，也可以先通过DLT求解完一次位姿再通过BA来进行优化，求得一个质量更高的位姿。也可以直接进行优化，如果相机连续运动幅度较小也可以这样做。如果是融了imu的话，也可以通过imu传播的位姿作为初值来进行BA优化。
在相机雷达融合的系统中，同样也可以融合一个雷达和一个单目相机，通过BA来构建重投影误差，进行多传感器融合的算法。

3D-3D，ICP

这个其实没什么好说的，如果已知两组3D点的匹配关系，是非常好去做ICP匹配的。而雷达并没有这样的匹配关系，往往只能通过构建kdtree来搜索最近邻，在优化位姿与搜索最近邻之间一直互相优化达到较好的匹配效果。
ICP解法可以有：

1. 基于SVD分解的方法
2. 基于优化的解法。

总结

这个算是重温14讲，记录自己的一些见解，把认为重要的部分以更加简洁的形式记录下来，复习巩固。