三维中通过一个点和距离与其欧拉角计算另一个点位置

在三维中计算一个点通过平移旋转的新点坐标

  在做三维交互的时候，我们也许会需要通过设定一些参数来计算一个三维点坐标到另一个点的变换过程；如，我们对点B（视锥体中心点）设置平移设置欧拉角：俯仰角(Pitch)、偏航角(Yaw)后，需要得到的点A的坐标位置，那么我们应该怎样来进行计算呢？

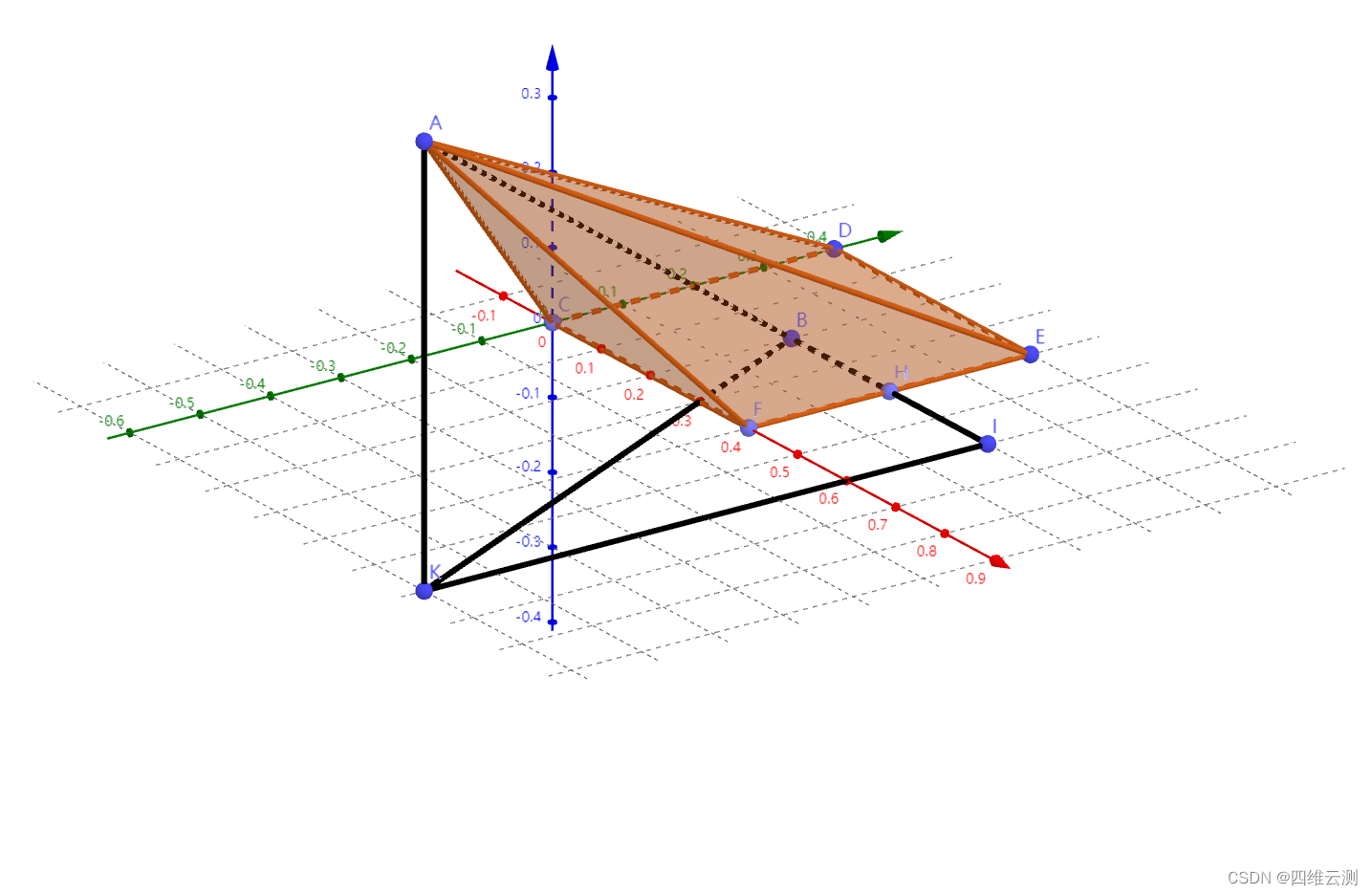
步骤分析

  这里我们是要通过F点设置角度与偏移来计算A点的坐标，那么上图中X的偏移量就应该为BI线段（x=BI），Y就应该为IK线段（Y=IK），Z则为AK线段（Z=AK）；通过这些信息我们可以很明显的看出来，角KAB就是我们的俯仰角(Pitch)，角KBI则是偏航角(Yaw)，当前我们已知的信息有AB之间的距离，俯仰角及偏航角。

那么通过分析得出：
KB = SIN∠KAB * AB
z轴偏移量：Z = AK = COS∠KAB * AB
x轴偏移量：X = BI = SIN∠IKB * KB
y轴偏移量：Y = IK = COS∠IKB * KB

这样我们就知道了通过设置俯仰角(Pitch)，偏航角(Yaw)和距离所偏移得到的点A的坐标了，那么下面就为大家把代码帖出来供大家取用。

代码实现

osg::Vec3f getNewPoint(osg::Vec3f pointB,double s_pitch,double s_heading, double s_dis)
{
	//这里原本向下为0度，此处减去90度是为了让俯仰角在平视时为0度
	float pitch = osg::DegreesToRadians(s_pitch - 90);
	//偏航角这里由于本人代码中需要进行反转所以将角度进行了反转
	float nAPYaw = (s_heading > 0) ? s_heading - 180 : s_heading + 180;
	float heading = osg::DegreesToRadians(nAPYaw);
	float len = s_dis * sinf(pitch);
	float delt_z = s_dis * cosf(pitch);
	float delt_x = len * sinf(heading);
	float delt_y = len * cosf(heading);
	osg::Vec3f spnt = pointB + osg::Vec3f(delt_x, delt_y, delt_z);
	return spnt;
}

到这里我们的点偏移计算讲解也就结束了，如果大家觉得我的方法还有用的话，也请大家能够点赞鼓励一下，您的鼓励是我分享的动力，谢谢各位！