t检验的几种常见类型及其应用条件

一、t检验定义

t检验用于两组定量数据资料的均数差异比较，在一般背景资料分析、基线分析中应用较为广泛。数据资料要求有一个两水平的定类数据用于分组，因变量要求为定量数据(连续型数据)。例如某研究欲比较不同性别新生儿体重有无差别，此时性别为定类数据用于分组，体重作为定量数据，作为目标变量或因变量。

由于t检验要求数据正态性，因此在t检验前应当先检验正态分布情况。一般来说，只要不是严重偏态，则t检验基本适用。否则可考虑对数据进行转换使其近似正态后再做检验，或者使用对应的非参数检验方法。

二、t检验类型

t检验包括三种类型：单样本t检验、配对样本t检验，以及独立样本t检验。三种t检验在选择时的注意事项如下表所示：

t检验	研究目的	适用条件	常见应用场景举例	SPSSAU分析路径
单样本t检验	一组数据的均数是否与给定常数之间存在差异	单样本服从正态分布	研究人员考察某地新生儿的平均体重与常模体重的差异	【通用方法】→【单样本t检验】 【实验/医学研究】→【概要t检验】
配对样本t检验	两组配对数据均数的差异比较	差值数据服从正态分布	体育疗法前后测定的舒张压有无差异	【通用方法】→【配对t检验】
独立样本t检验	两组独立数据均数间的差别比较	两样本分别服从正态分布且要求方差齐性	干预组与对照组人群的心肌血流量有无差别	【通用方法】→【t检验】 【实验/医学研究】→【概要t检验】

有些研究在没有原始数据，仅有样本量、均值、标准差统计结果的情况下，仍然需要采用t检验进行差异比较，这一过程通常称为概要t检验，常见的用法比如概要单样本t检验、概要独立样本t检验。

SPSSAU平台在【通用方法】、【实验/医学研究】模块下，共提供4个独立的模块来完成各种类型的t检验。

三、正态性与方差齐性

t检验要求进行差异比较的数据须是定量数据，且要求数据服从或近似正态分布，独立样本t检验还另外要求两组数据的方差齐性。

1. 正态分布

数据服从或近似正态分布，是t检验的基础条件。实际分析时可以用图形法或显著性检验法判断该条件是否满足，图形法比如绘制直方图、正态P-P图、Q-Q图对正态分布进行直观判断，此类方法判断标准较为宽松，有一定主观性；显著性检验法则主要包括Kolmogorov-Smirnov检验和Shapiro-Wilk检验。

正态分布图示法检验可具体分为以下四种，分别是直方图、PP图或QQ图、核密度图，如下表格所示：

项	图	特点
1	直方图	检验各分组数据分布特征进行判断
2	PP图	查看真实数据与理论正态分布数据累计概率是否一致进行判断
3	QQ图	查看真实数据与理论正态分布数据分位数是否一致进行判断
4	核密度图	直观查看数据分布特征进行判断

（1）直方图

直方图是一种数据分布的可视化展示，其数学原理为将数据分为多个组别，然后累计汇总各个组别的样本数量，并且进行展示。如果数据具有正态性特质，那么应该呈现出‘钟型、两头低、中间高’的分布形状，如果直方图基本呈现出此特征即说明具有正态性。

（2）P-P图&Q-Q图

接着关于PP图和QQ图的原理及实现说明，PP图的原理是对比真实数据与理论正态分布数据分别的累计概率值，如果说数据具有正态性，那么真实数据的累计概率值应该与理论正态分布数据的累计概率值基本保持一致，反之如果说数据不满足正态性，那么真实数据的累计概率值与理论正态分布数据的累计概率值应该有很大差别。将真实数据的累计概率值，与理论正态分布数据的累计概率值绘制散点，如果数据符合正态性，那么散点应该呈现出一条对称线。反之，散点应该明显偏离对称线。

与PP图类似，QQ图也是对比真实数据与理论正态分布数据是否具有一致性，但QQ图时，其对比分位数点（PP图对比累计概率值）。关于QQ图检验数据是否呈现出正态性特质，其与PP图基本一致，如果散点呈现出一条对称线，那么说明数据具有正态性，反之如果散点明显偏离对称线则说明不具有对称性。PP图或QQ图的绘制，可通过SPSSAU【可视化】模块中PP/QQ图找到，接着以身高数据为例进行绘制PP图或QQ图。

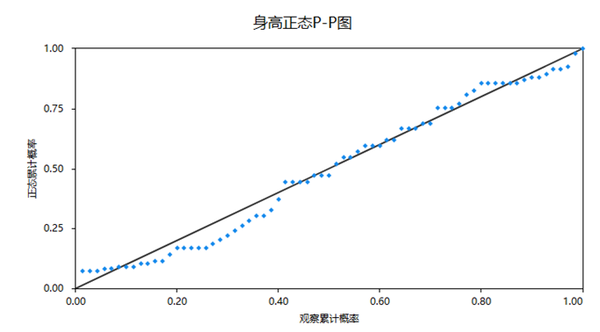
上图为身高数据绘制的PP图，图中横坐标为真实身高数据的累计概率（比如小于1.8米的样本百分比），纵坐标为理论正态分布数据的累计概率（比如理论上小于1.8米样本百分比）。上图中散点基本均在对称线上，意味着真实身高数据累计概率，与理论正态分布的身高数据累计概率基本一致，因而说明数据具有正态性。反之如果多数的散点远离对称线，则说明不具有正态性。

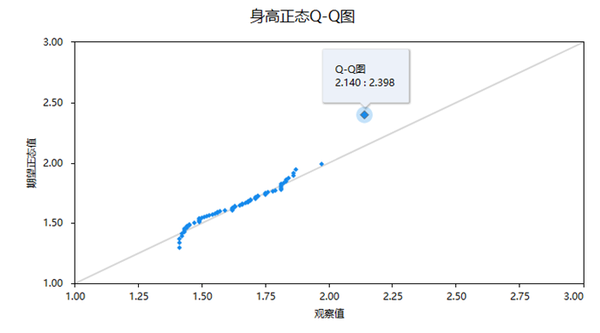
上图为身高数据绘制的QQ图，图中横坐标为真实身高数据的观察值（即真实身高数据），纵坐标为理论正态分布数据的分位数值（关于分位数值：比如真实数据中有30%的人小于1.7米，那么该30%数据时应该对应理论数据的值是1.72，此处1.7米即为真实身高数据的观察值即分位数值，1.72即为理论正态分布数据的分位数值）。上图中散点基本均在对称线上，意味着真实身高数据观察值，与理论正态分布的身高数据分位数值基本一致，因而说明数据具有正态性。反之如果多数的散点远离对称线，则说明不具有正态性。但从上图还可以看到真实身高为2.140米时，该值明显偏离对称线，如果将该值进行剔除，可能数据会展示出更好的正态性。

样本数据完全服从正态分布过于理论化，实际分析中数据出现一定偏态较为常见。t检验、方差分析等参数检验方法对正态分布要求相对稳健，轻微或中等程度的偏态对最终检验结果的影响并不大。

除了图示法检验正态分布，还可以进行统计检验。

正态分布检验法通常包括以下三种，分别是Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Jarque-Bera，如下表格所示：

项	检验	特点
1	Kolmogorov-Smirnov检验	通常适用于大样本
2	Shapiro-Wilk检验	通常适用于小样本
3	Jarque-Bera检验	通常适用于大样本

一般来讲，如果样本较大（比如样本大于50），那么使用Kolmogorov-Smirnov检验较为适合，如果数据量为小样本（比如样本小于50），那么使用Shapiro-Wilk检验较为适合。此处样本的大小标准并无数学角度的划分标准，建议研究者可结合图示法综合判断。Jarque-Bera检验原理上是针对偏度和峰度数据进行拟合优度判断，由于偏度和峰度数据通常只能在大样本数据时才能很好的识别正态性物质，因而Jarque-Bera检验也只适用于大样本数据。关于上述三个检验，可经【通用方法】→【正态性检验】得到, 接着以身高数据为例进行说明。

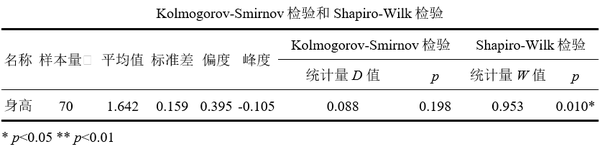
Kolmogorov-Smirnov检验的原假设为数据具有正态性，因而如果接受原假设即p值>0.05，那么就说明数据具有正态性，反之p值<0.05则说明数据不具有正态性。上表格中p值=0.198>0.05，那么说明身高数据具有正态性，这一结论与图示法表现出一致性。

与此同时，Shapiro-Wilk检验的原假设为数据具有正态性，此处p值=0.01<0.05即拒绝原假设，按Shapiro-Wilk检验标准，身高数据并不具有正态性。因而在分析时需要注意检验的适用性，如果按照Shapiro-Wilk检验适用于小样本（比如样本小于50作为标准），那么就不应该关注该检验指标。

Jarque-Bera检验的原假设为数据具有正态性，因而如果接受原假设即p值>0.05，那么就说明数据具有正态性，反之p值<0.05则说明数据不具有正态性。上表格中p值=0.399>0.05，那么说明身高数据具有正态性，这一结论与图示法表现出一致性。

2. 方差齐性

方差齐性，也称为方差齐次或简称为方差齐，该检验假设两组数据的总体方差相同，利用F检验进行统计推断。按α=0.05显著性水平，当F检验的概率p值大于0.05时认为两组数据的方差齐；当p值小于0.05时两组数据的方差不齐。

独立样本t检验要求正态性同时还要求两组数据的方差齐性，方差不齐时需要对t检验的结果进行校正。因此t检验时，应根据方差齐性检验的结论，选择t检验或校正后的t检验显著性结果。

使用【通用方法】→【t检验】模块进行独立样本t检验时，平台会自动判断方差齐性条件，并输出对应的t检验结果。如果用户需要单独做方差齐性检验，可通过【通用方法】→【方差】模块实现。

此处结合具体案例进一步介绍方差齐性检验的操作与结果解读。

方差齐检验案例操作与分析结果解读

【例4-1】某研究收集到100例儿童的腰围(cm)数据，其中肥胖组50例，用数字1表示组别，另外50例为非肥胖组，用数字0表示，试分析两组数据的方差是否相等。

1) 方差齐性检验

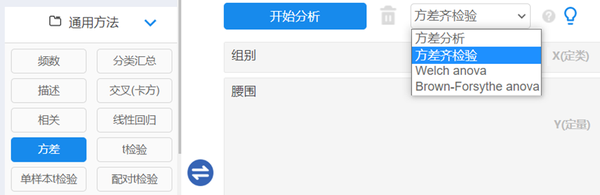
数据读入平台后，在仪表盘中依次选择【通用方法】→【方差】模块，将“组别”变量拖拽至【X(定类)】，“腰围”变量拖拽至【Y(定量)】分析框内，方法下拉框内选择【方差齐检验】，操作界面如图 4‑1所示，最后单击【开始分析】。

2）结果分析

两组数据的方差齐分析结果见上表，F=2.576，p=0.112﹥0.05，表明两组数据的方差齐。

以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。