一、Fisher确切概率
Fisher确切概率法是由R.A.Fisher(1934)提出的,其理论依据是超几何分布,是一种直接计算概率的假设检验方法。由于其在四格表中应用最为广泛,所以也直接称为四格表确切概率,此外它也可在R×C表卡方检验条件不满足时使用。
1. 2×2四格表资料
当2×2四格表资料出现E≤1或n﹤40情况时,可使用Fisher确切概率进行假设检验。此外当四格表卡方检验后所得概率p值接近检验水平α时,亦可使用Fisher确切概率。
【例4-11】四格表Fisher确切概率。将23名抑郁症患者随机分到两组,分别用两种药物治疗,结果见表 4-35,问两种药物的治疗效果是否不同。数据来源于方积乾(2012),数据文档见“例4-11.xls”。
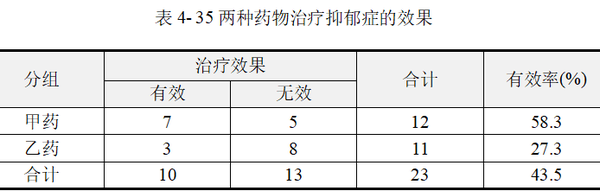
(1) 数据与案例分析
数据文档为加权数据格式,根据适用条件,本例四格表资料的样本量n﹤40,Pearson卡方、Yates校正卡方不再适用,宜采用Fisher确切概率法进行分析。
(2)卡方检验
四格表资料的Fisher确切概率可直接通过【卡方检验】模块实现,将“组别”拖拽至【X(定类)】,“疗效”拖拽至【Y(定类)】。本例需加权处理,故再把“频数”拖拽至【加权项(可选)】。选项框内模型选择【百分数(按列)】,最后单击【开始分析】。
本例n = 23﹤40,且有单元格1≤E﹤5。因此Fisher确切概率结果更为可靠。如表 4-36所示,确切概率p=0.142,在α=0.05检验水平上尚不能认为两药治疗抑郁症的效果不同。

2. R×C列联表资料
R×C列联表Pearson卡方检验要求列联表中所有的单元格理论频数不应小于1,并且1≤E﹤5的单元格数量不宜超过总数的1/5。如果出现不符合该条件的情况,研究者可考虑采用Fisher确切概率法进行差异检验。
在SPSSAU中,可通过【实验/医学研究】下的【卡方检验】或【fisher卡方】两个模块实现Fisher确切概率法。
【例4-12】R×C表Fisher确切概率。某研究回顾性分析62例NME乳腺癌患者MRI影像及临床病理资料,其中不同分子亚型在有无瘤周水肿的分布数据见表 4-37。试分析四种亚型在瘤周水肿的分布有无差别。数据来源于晋瑞,张冰等 (2019),数据文档见“例4-12.xls”。

(1) 数据与案例分析
本例数据是4×2列联表数据,有8个单元格频数,总样本量n=62﹥40。通过【卡方检验】模块进行分析后,我们发现1≤E﹤5的单元格数比例为37.5%,超过了1/5的单元格数,Pearson卡方不再适用,此时宜采用Fisher确切概率法进行检验。
(2)Fisher确切概率
【卡方检验】模块只提供2×2四格表资料的Fisher确切概率,针对R×C列联表我们使用【Fisher卡方】模块。该模块无需录入数据,而采取直接输入频数数字的方式进行假设检验。
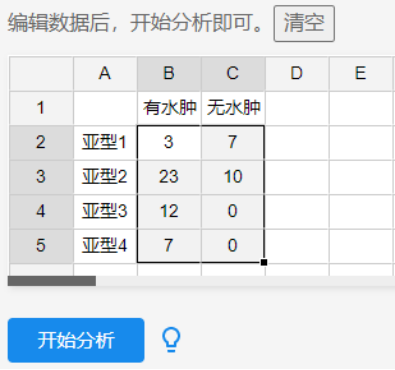
图 4-15 Fisher确切概率操作界面
在仪表板中依次选择【实验/医学研究】→【Fisher卡方】模块,在电子表格区域直接手动输入案例数据,具体设定如图 4-15所示,最后单击【开始分析】。
(3)结果分析
特别强调,Fisher确切概率法是直接计算假设检验的p值,因此中间并无统计量,结果如表4-38所示。
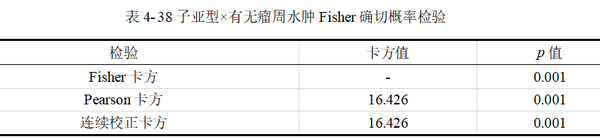
经计算,本例Fisher确切概率p值=0.001﹤0.05,认为四种不同分子亚型在留瘤周水肿上的分布差异有统计学意义。
二、配对卡方检验
前面介绍的是成组设计的卡方检验,比如两组或多组率的比较,此处的组就是各自独立的对象。与成组设计对应的是配对(或配伍)设计。
配对设计的特点是对同一样本分别用A和B两种方法处理,或是对样本前后测量,观察其水平分布的差异或一致性。若采用配对设计,结局指标为计数资料时,则需要采用配对设计的卡方检验方法。
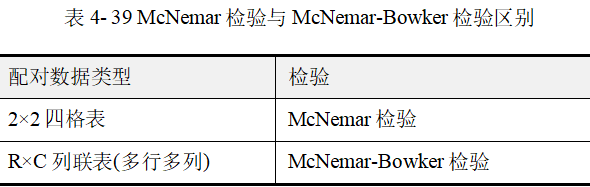
如果是配对四格表资料,则使用McNemar检验;其他非四格表的配对资料,则使用McNemar-Bowker检验,二者的区别如下表 4-39。
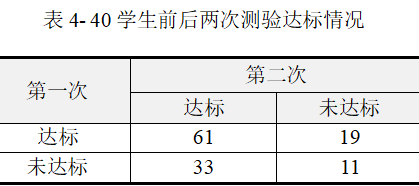
【例4-13】124个学生1000米长跑,训练一个月前后两次测验达标情况如下表 4-40所示,问一个月的训练是否有显著效果?数据来源于王孝玲(2007),数据文档见“例4-13.xls”。
(1)数据与案例分析
数据文档为加权数据格式,包含3个变量。标题分别为“第一次测验”、“第二次测验”和“频数”,两次测验的结局均为“达标”和“未达标”。每个学生均有前后两次测验,并且测验的结局均为“达标”或“不达标”,这是配对设计的定类数据资料。综合这两点,不适用于前面学习的普通成组设计的卡方检验,而应采用专门用于配对设计的卡方检验方法。
(2)配对卡方检验
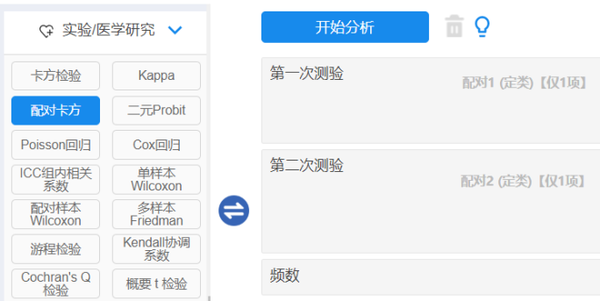
数据读入平台后,仪表盘中依次选择【实验/医学研究】→【配对卡方】模块,将“第一次测验”拖拽至【配对1(定类)仅1项】,将“第二次测验”拖拽至【配对2(定类)仅1项】,然后用“频数”作为【加权项(可选)】,操作界面见图 4-16,最后单击【开始分析】。
(3)结果解读
四表格资料的配对设计使用McNemar检验;如果配对数据的组别大于2即配对多分类时,则使用McNemar-Bowker检验。
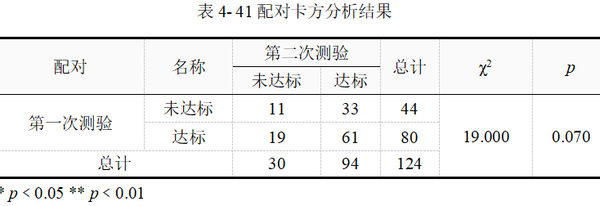
本例为McNemar检验,结果见表 4-41。χ2=19.00,p=0.07﹥0.05训练前第一次测验结果与训练后的第二次结果无差异,或差异无统计学意义。
以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究,书中不仅涵盖了数据清理、统计分析和模型构建等内容,还提供了丰富的案例,以便于读者在实际研究中应用。























 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








