相关分析入门知识与分析步骤，三类相关系数：Pearson、Spearman、Kendall

两个变量之间独立指的是二者间完全没有关系，两个变量之间相关，指的是二者间存在不确定性关系。此处相关关系不同于确定性关系，确定性关系一般指函数关系，当自变量给定，则函数值确定。而不确定性的相关关系，通俗理解即一个为自变量，另一个为随机变量或者两个都是随机变量，当一个变量变化时，另一变量的取值有一定的随机性变化。

例如收集同一家企业1000名职工的工资和受教育数据，每个人的受教育年限不同，工资也不同，此时这两个变量都是随机变量。很多研究文献证实工资和受教育年限存在相关性，或者说一名职工的工资受他接受教育时长的影响。当受教育年限改变时，工资水平也相应随之改变，即不同的受教育程度其获得的工资水平不完全相同，有一定的随机性。

职工工资受其教育程度影响，但工资与受教育年限并非严格的因果关系。我们可以说工资与受教育年限存在相关性，也可以说接受教育的程度影响职工工资。

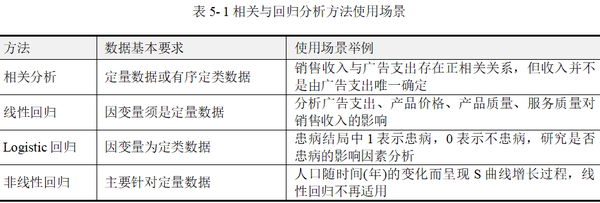
本章节介绍研究分析中的相关与影响关系，主要包括相关分析、线性回归、Logistic回归，以及非线性回归，各方法数据要求及使用场景举例如表 5-1所示，接下来在各节内容中结合具体案例展开阐述。

一、相关分析概述

相关分析是用来研究两个或多个变量间的相关关系的统计学方法。例如分析销售收入与广告支出间的相关关系，或者销售收入、广告支出、产品价格、产品质量、服务质量之间的相关关系。变量之间可以是同等地位的，也可以区分为一个或多个自变量对因变量的影响关系。

1. 线性、非线性与无相关

相关关系按不同的划分方式可以有多种类型，结合直线趋势与关系密切程度将相关关系分为正线性相关、负线性相关、非线性相关、无相关4种类型，见图 5-1。

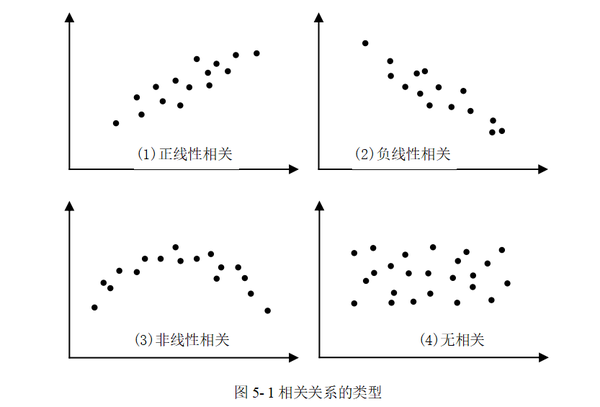
两个变量间的关系在散点图中的点总体上呈现出一条直线，称之为线性相关。上图中的(1)表示一个变量增加或减少，另一个变量相应线性增加或减少，称为正线性相关(简称正相关)；上图中的(2)表示一个变量增加或减少，另一个变量反而线性减少或增加，称为负线性相关(简称负相关)。

两个变量间的关系在散点图中的点不是一条直线时，称之为非线性关系或曲线相关，见上图中的(3)。两个变量彼此互不影响，其数量变化各自独立，称为无相关，见上图中的(4)。

2. 认识线性相关系数

两个变量间的关系在散点图中的点总体上呈现出一条直线，称之为线性相关，包括正相关和负相关，Pearson相关系数是衡量变量之间线性相关关系密切程度和方向的统计指标。

Pearson线性相关系数，又称皮尔逊积差相关系数，通常被简称为相关系数，一般用r表示。r的取值为-1≤r≤1，绝对值越大表示相关密切程度越高。

根据贾俊平(2014)，对于一个具体的

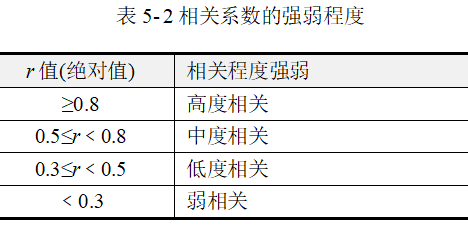
• r 绝对值，≥0.8视为高度相关；
• 0.5≤r﹤0.8可视为中度相关；
• 0.3≤r﹤0.5 表示低度相关；
• ﹤0.3 说明两个变量之间是弱相关

具体见表 5-2。r为正数时，表示两变量的变化方向一致，称为正相关，r为负数时，表示两变量的变化相反，称为负相关。

例如，某省份国民收入与居民储蓄存款余额r=0.9，表明二者是高度正相关关系，国民收入增加则居民储蓄存款余额也随之增加，反之国民收入减少则居民储蓄存款余额也随之减少。

实际分析中我们是基于样本数据计算相关系数，用于估计总体相关系数时必定存在抽样误差，因此相关系数须通过显著性检验才能说明其成立与否。一般上是先假设总体相关系数为0，只要相关系数的显著性概率p值小于0.05，则表明实际相关系数明显不等于0，可说明相关关系存在。

3. 如何选择线性相关系数

除Pearson相关系数之外，常用的相关系数还有Spearman相关系数、Kendall相关系数。

三个相关系数在具体使用时可参考图 5-2，选择恰当的相关系数进行相关分析。

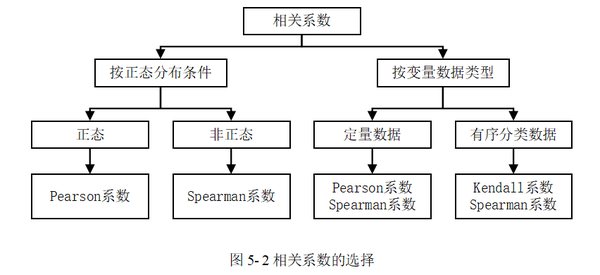
（1）Pearson相关系数：适用于两个变量均为定量数据的情况，要求数据服从二元正态分布，通常我们简化为两个变量分别服从正态分布，并且无明显异常值。可以借助图形法或更为严格的正态性检验方法判断该条件，一般来说，不是严重违反正态分布时仍然可以继续使用Pearson相关系数，多数情况下结果较为稳健。

（2）Spearman相关系数：又称为秩相关系数或等级相关系数，适用于定量数据或等级(有序分类)数据，是用两个变量的秩次大小做相关分析。其对数据分布没有明确要求，属于非参数方法。在进行相关分析时，当Pearson系数不满足正态性条件时，Spearman相关系数用作Pearson相关系数的非参数替代。

（3）Kendall相关系数：同样是用秩次进行相关分析，也属于非参数方法，适用于连续性数据或等级(有序分类)数据，主要用于把两个有序分类变量的相关性。也称作和谐系数，可以用作一致性分析。

4. 线性相关系数的报告

计算相关系数后，应予准确解读和报告。一般来说解读及报告时应按顺序包括以下三个方面：

(1) 先解读相关系数显著性检验的概率p值，当p值小于0.05时认为存在相关关系；

(2) 接着解读相关系数的正负方向，相关系数为正数则为正相关，负数则为负相关；

(3) 最后解读相关系数绝对值的大小，明确相关关系的密切程度。

二、相关分析步骤

变量的数据类型，以及是否服从正态分布对相关分析过程有一定的影响，相关分析的一般步骤如图 5-3所示。

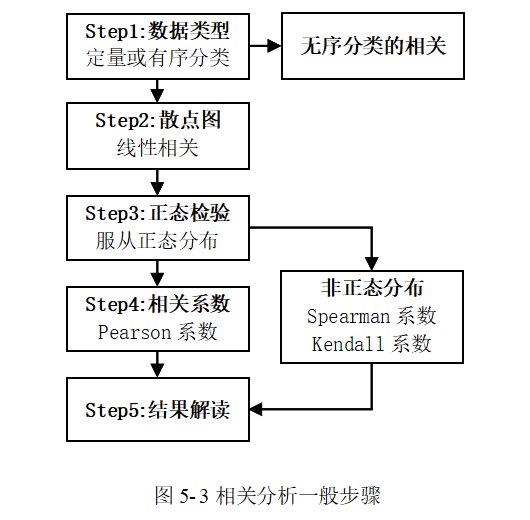
(1) 数据类型

本节主要介绍的Pearson、Spearman以及Kendall系数主要针对定量数据和有序分类数据的相关分析，如果遇到两个无序分类变量间的相关关系，可通过卡方检验输出列联系数或Phi and Cramer's v系数实现。

(2) 散点图

散点图能直观观察变量间的变化关系，开始相关分析前先绘制两个变量的散点图，观察和判断两变量存在线性相关还是非线性相关，本节介绍的内容适于线性相关的情况。

(3) 正态检验

对于定量数据，先通过直方图、PP图、QQ图等图形法，或者正态分布检验法判断数据分析状况。

(4) 相关系数

根据正态分布条件以及变量数据类型，对于两个定量数据且满足正态性的情形，一般选择Pearson相关系数，如果严重偏态则考虑使用Spearman相关系数；对于两个有序分类数据，一般选择Kendall相关系数。

(5) 结果解读

对相关系数的显著性、相关的方向、相关的程度进行正确解读。有多个数据进行两两相关分析时，可报告和分析相关系数矩阵。

在呈现相关系数时常用“*”符号在相关系数r右侧标注其显著性水平，当显著性检验的p值﹤0.05时，标注“*”；当显著性检验的p值﹤0.01时，标注“**”；当显著性检验的p值﹤0.001时，标注“***”。

以上内容摘自《SPSSAU科研数据分析方法与应用》第5章——相关影响关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。