工业过程建模与先进控制（二）多变量分析

理解配对选择问题有助于了解模型预测控制（MPC，Modeling Predictive Control）的优势，如果掌握了MPC方法就不用配对了。一般来说，一个输出主要受一个控制输入的影响。耦合系统存在相互影响（interaction）。对于有多个输入多个输出的混合系统来说，哪个输出选择和哪个输入配对就是变量“pairing”问题。

目录

为什么要配对

相对增益的定义 Relative gain（RGA）

RGA的性质

相对增益符号的含义

相对增益值的含义

RGA的敏感性问题

相对增益作为nominal process中的扰动

负的相对增益

对模型不确定性的敏感性

Matlab中的RGA计算

---

为什么要配对

1. 配对解耦后的SISO系统设计起来更好理解。
2. 硬件和软件已经适用于SISO控制器设计了。

相对增益的定义 Relative gain（RGA）

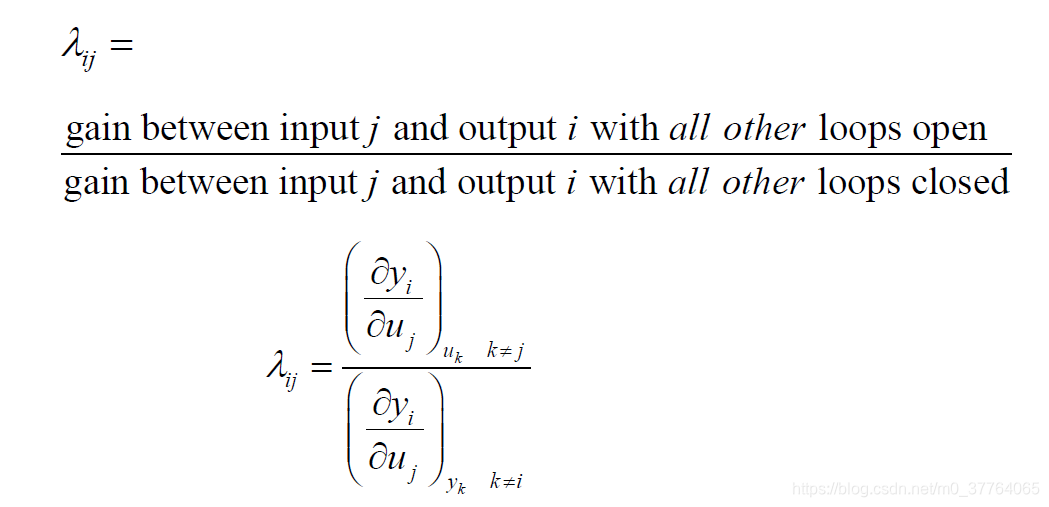
RGA的性质

RGA的每行和为1.0，列和也为1.0。因此对于2×2系统，只需要计算1个相对增益就能求出整个矩阵；对于3×3矩阵，计算4个元素就可以求出所有的9个元素。

相对增益符号的含义

一般不将配对增益为负的输入i和输出j组合在一起。

例如，假设输入1和输出1的开环增益是正的，控制器增益是负的。那么负的相对增益意味着如果回路2闭环，那么回路1需要一个正的控制器增益。而一个需要根据别的回路是否闭合而改变控制器增益符号的控制系统并不是我们期望的。

相对增益值的含义

栗子：y1=k11*u1+k12*u2,y2=k21*u1+k22*u2。以u1和y1组合的增益为例。

1、相对增益>1

分子>分母，说明当回路2开环时u1和y1的增益比回路2闭环时大。

• 如果在回路2开环时设计u1-y1的控制器，闭合回路2时，有效过程增益会比u1-y1的增益小，因此会出现一个迟缓现象。
• 如果在回路2闭环时设计u1-y1的控制器，断开回路2时，由于u1-y1的增益会比调谐时的控制器增益大，因此会破坏稳定。

2、0<相对增益<1

分子<分母，说明当回路2闭环时u1和y1的增益比回路2开环时大。情况刚好和上述相反。

RGA的敏感性问题

当调节一系列SISO控制器来组成多变量-SISO系统时，如果一个回路在别的回路闭合的情况下运行良好，还要考虑当别的回路断开的情况。

相对增益作为nominal process中的扰动

（a）回路2开环时的过程增益

（b）回路2闭环时的有效过程增益（Effective process gain）

1、0<相对增益<1

说明k11,eff比k11大。

• 如果回路1的控制器设计基于k11（假设此时回路2开环），那么当回路2闭合时，回路1的控制器增益kc1应该detuned by a factor of lamda11，否则系统会响应太迅速导致不稳定。
• 如果回路1的控制器设计基于回路2闭环时，那么当回路2断开时，kc1应该增加1/lamda11倍。问题在于kc1此时变大了，当回路2再次闭合时，又有可能不稳定了。

为了安全起见，如果相对增益小于1，应根据回路2的闭环情况调整回路1。

2、相对增益>1

说明k11,eff比k11小。

• 如果回路1的控制器设计基于k11（假设此时回路2开环），那么当回路2闭合时，回路1的控制器增益kc1应该increased by a factor of lamda11，否则系统会响应太迅速导致不稳定。问题在于kc1此时变大了，当回路2再次断开时，又有可能不稳定。
• 如果回路1的控制器设计基于回路2闭环时，那么当回路2断开时，kc1应该减少1/lamda11倍。

为了安全起见，如果相对增益大于1，应根据回路2的开环情况调整回路1。

负的相对增益

• 失效敏感性

一个建立在具有负的相对增益的配对的控制策略具有失效敏感性，是不可取的。

• 子系统的含义

例如，如果回路1失效了，除去回路1的子系统的RGA仍然满足所有配对增益为正的要求。

对模型不确定性的敏感性

较大的相对增益（25或更高）对模型不确定性极端敏感，此时某些回路只能断开，只能仅使用部分控制回路。

Matlab中的RGA计算