支持向量机（SVM）之超平面（Hyperplane）

超平面（Hyperplane）是支持向量机（SVM）中一个关键概念，特别是在分类任务中。以下是关于超平面的详细解释：

什么是超平面？

在n维空间中，一个超平面是一个（n-1）维的子空间。例如：

• 在二维空间中，超平面是一条直线。
• 在三维空间中，超平面是一个平面。

SVM中的超平面

在SVM中，目标是找到一个将不同类别的样本分开的最优超平面，使得到超平面最近的点（支持向量）的距离最大化，即最大化分类间隔。

最优超平面

分类间隔

分类间隔（Margin）是指超平面与最近的样本点（支持向量）之间的距离。SVM通过最大化这个间隔，找到一个泛化能力更强的分类器。

支持向量

支持向量是指那些位于分类间隔边界上的样本点。这些点对超平面的确定起到关键作用，因为如果移除这些点，超平面的位置将会改变。

非线性可分的数据

对于非线性可分的数据，SVM引入了核函数（Kernel Function），将原始数据映射到高维空间，在高维空间中寻找线性可分的超平面。常用的核函数包括：

• 线性核（Linear Kernel）
• 多项式核（Polynomial Kernel）
• 径向基函数核（RBF Kernel）
• Sigmoid核

软间隔SVM

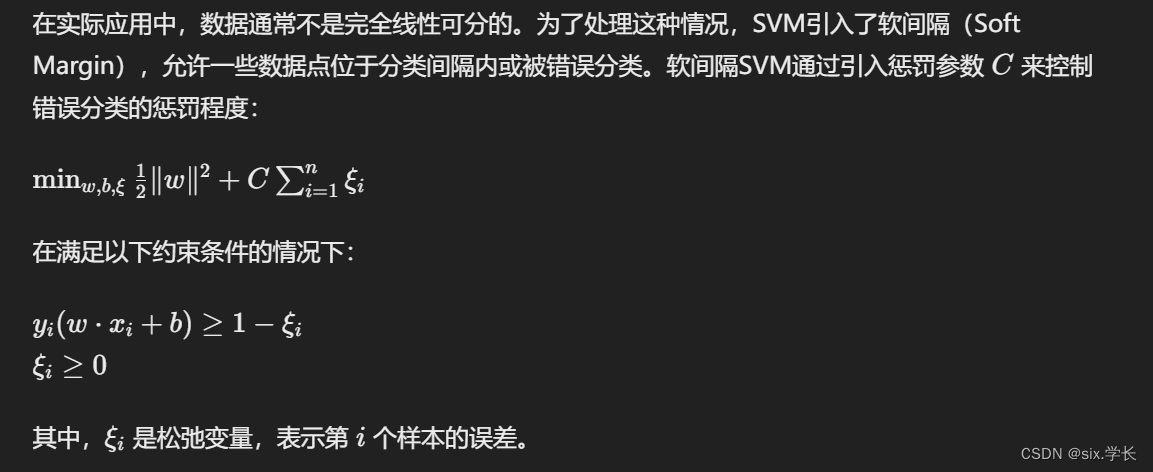
举例说明

假设我们有一个二维数据集，包括两类样本。我们希望使用线性SVM对其进行分类。

import nump