二维光场分析

一、单色光波长的复振幅表示

实波函数

复波函数

复振幅

 由于时间因子相同，可以用复振幅来描述

光强

1.1 球面波的复振幅（单色点光源发出的光波）

等相位面是同心球面，波矢处处与等相位面垂直，即

是 r = 1 处的振幅

发散球面波：

会聚球面波：

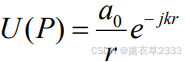
 球面光波在整个空间中, 沿任何方向上的空间频率均为1/, 沿任何方向上的空间周期均为。

 1.2 平面波的复振幅

在整个空间中：

① 传播方向相同，即仅有一个波矢方向

② 等相位面是平面，总是与波矢垂直

③ 振幅处处相等，是常数

 单色平面波的复振幅：

令

 在xy平面上的复振幅分布表示为

平面波的线性相位因子 

        等相位线是一组平行等距的平行斜线, 由于相位值相差2Π的各点的光振动实质上是相同的, 所以平面上复振幅分布是以2Π为周期的周期分布。

 实际上，单色平面波与单色球面波的获取：

 二、平面波的空间频率

2.1 k位于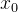z平面内

 复振幅在xy面上的空间周期可以用相位差2Π的两相邻等相位线的间距 X 表示

 用空间周期的倒数表示 x 方向单位长度内变化的周期数，即

 因y 方向空间周期为无穷，空间频率为0，则平面波复振幅为：

2.2 任意方向传播的平面波

在平面上的空间频率

 相应的空间频率分别为

 平面波复振幅

 2.3 整个空间

z方向的空间频率

复振幅分布

1/表示平面波沿传播方向的空间频率。

三、复振幅分布的空间频率(角谱)

         物函数g(x,y)可以分解为无穷多个不同频率(,)，不同取向（ = /） ，不同权重G(,)dd的指数基元。

        指数基元 exp[ j2π (ξx +ηy)]代表一个传播方向余弦为 cosα = λξ，cos β = λη 单位振幅的单色平面波。因此，物函数 g ( x , y ) 可以看作不同传播方向的单色平面波分量的线性叠加。

        G(ξ,η) 为复振幅分布 g(x, y)的空间频谱,方向余弦表示

这里将平面波的空间频率与特定的传播方向相对应，

 称为平面波的角谱。