可以说是“例行”碎碎念了吧
不知不觉已经颓了三个星期了,驾驶员已经是最后值得讨论的一个我其实也是似懂非懂,希望大佬经过能留下只言片语的一个部分。(没错,我就是颓废一周,起来整理一晚上)
这个部分对于我的实际稳定性控制来说其实是不需要的,加上反而会造成一些耦合的情况,但我开题的时候就很想整一个,那中期只能咬牙给完成了。终期联合控制也都是辛酸泪,唉。
公式等可能有误,请谨慎参考,若有疏漏,请批评指正!
前言
驾驶员模型我主要参考的书目是郭孔辉的《汽车操纵动力学》,主要参考的论文是任晨辉的《基于底盘协同的电动轮驱动汽车横向稳定性控制》和高振海的《汽车方向预瞄式自适应PD控制算法》。
由于我自身能力有限,毕业设计时长也有限,理解并不是很透彻。具体体现在目标预期轨迹坐标(或称预瞄点坐标)的获取。我的方法是通过坐标系的变换,查表(目标轨迹曲线)获得,具体在理论模型的论文截图中体现。
以下是模型展示。

△ 建成这样主要是为了方便看仿真数据,好看看哪里出错

△ 我希望某天能拥有这个shai的轿车
1. 理论模型
驾驶员模型模拟真实驾驶员对车辆的动力或转向的操纵,本文假定理想车辆纵向车速恒定,则驾驶员模型的输出仅为方向盘转角。本文使用郭孔辉教授的单点预瞄驾驶员模型,“单点预瞄”即通过模拟驾驶员基于当前汽车行驶状态,对比未来预瞄时间点轨迹与目标轨迹的偏差,做出判断,滚动调节。该模型同时考虑了驾驶员反应的滞后和校正环节,前者包括驾驶员的神经反应滞后时间和驾驶员手臂和方向盘惯量等的滞后。
在驾驶员目标行驶轨迹已知的前提下,驾驶员理想侧向加速度的预瞄如图3-2所示。其中,XOY为大地坐标系,xOy为相对坐标系,二者原点重合;则"X(t)" 、“Y(t)” 为车辆质心的绝对坐标,“x(t)” 、“y(t)” 为车辆质心的相对坐标,单位均为m;“ψ” 为车辆航向角,单位为rad。

△ 图源:《汽车方向预瞄式自适应 PD 控制算法》
 △ 图源:我的毕设论文
△ 图源:我的毕设论文
由《汽车操纵学》,Gay=V2/L,其中,L为轴距。
2. Simulink模型

△ 此处重新展示模型
驾驶员模型的Simulink模型同样经历了两个版本,模型的变换主要还是为了更好的检查和修改数据。驾驶员模型需要调整的参数分别是驾驶员的目标轨迹(正常不用“调整”,但我需要在转弯前完成加速,导致我需要调整进入双移线工况的纵向偏移距)和预瞄时间 T,为简化模型,其余反应及调整时间均设为0。
以下为计算大地坐标系上的速度分量的代码片,输出后通过积分模块可获得大地坐标系下的坐标。
function [X_dot,Y_dot,V] = fcn(Vx,Vy,yaw)
V=sqrt(Vx^2+Vy^2)+eps;
X_dot=Vx*cos(yaw)-Vy*sin(yaw);
Y_dot=Vx*sin(yaw)+Vy*cos(yaw);
以下MATLAB Function的代码片通过调整预瞄时间T,即Tp,获得理想侧向加速度。我的导师说双移线工况的预瞄时间是1.1~1.3s,但我通过调参,很艰难的确定下最终预瞄时间为0.8,导师实在是太忙了,,我也不太清楚为什么会这样,大家可以自己调调参。
function [y_dd,Y_tp] = fcn(X_d,X,Y,yaw,Vy)
Tp=0.8;
y=-sin(yaw)*X+cos(yaw)*Y;
X_tp=X+X_d*Tp;
desire_road_Y = [0 0 0 0.1 0.7 1.8 2.8 3.4 3.5 3.5 3.3 2.4 1.1 0.2 0 0 0];
desire_road_X = [-10 0 305 310 315 320 325 330 335 350 355 380 385 390 395 400 700];
Y_tp = interp1(desire_road_X,desire_road_Y,X_tp,'linear');
y_tp=-sin(yaw)*X_tp+cos(yaw)*Y_tp;
y_d=Vy*cos(yaw);
y_dd=(y_tp-y-y_d*Tp)*2/Tp^2;
3. CarSim验证
原本的CarSim验证我也想和第二部分一样一句带过,但是等有人问的时候再解答就有点被动了。隔了这么久我其实已经忘得差不多了,但是我之前又实在是不想从躺平的状态起来,唉。
最近有点忙,但是又不想拖太久了,这个冷饭隔太多天了。又想着验证部分做完整一点,就各种找过程文件,恢复过程设定(有时候图方便,直接改动用于其他用处)。结果就是,我从开机到找到模型花了我一个半小时,我的用电脑状态变成跷二郎腿看手机等程序,我都笑了。。。那就进入可能不太完整的正题吧!
本部分书写顺序是按照笔者恢复文件的顺序书写,阅读顺序请按part1-part2来
part2
图3-3是对照组的Simulink界面,注释掉的部分是Simulink模型的控制部分,先放对照组主要是因为我最后验证的为对照部分,保存的也是对照部分。从此图可以看出本人在拟合最优参数时做出的尝试。

△ 此处输出mat文件而后通过MATLAB命令出图
CarSim主界面如图3-4所示,其中,Test Specifications部分不需要更改参数,因为我们“驾驶”的是同一辆车,如图3-5所示。

△ Plot部分并没有用,因为我是通过Simulink出的对比图
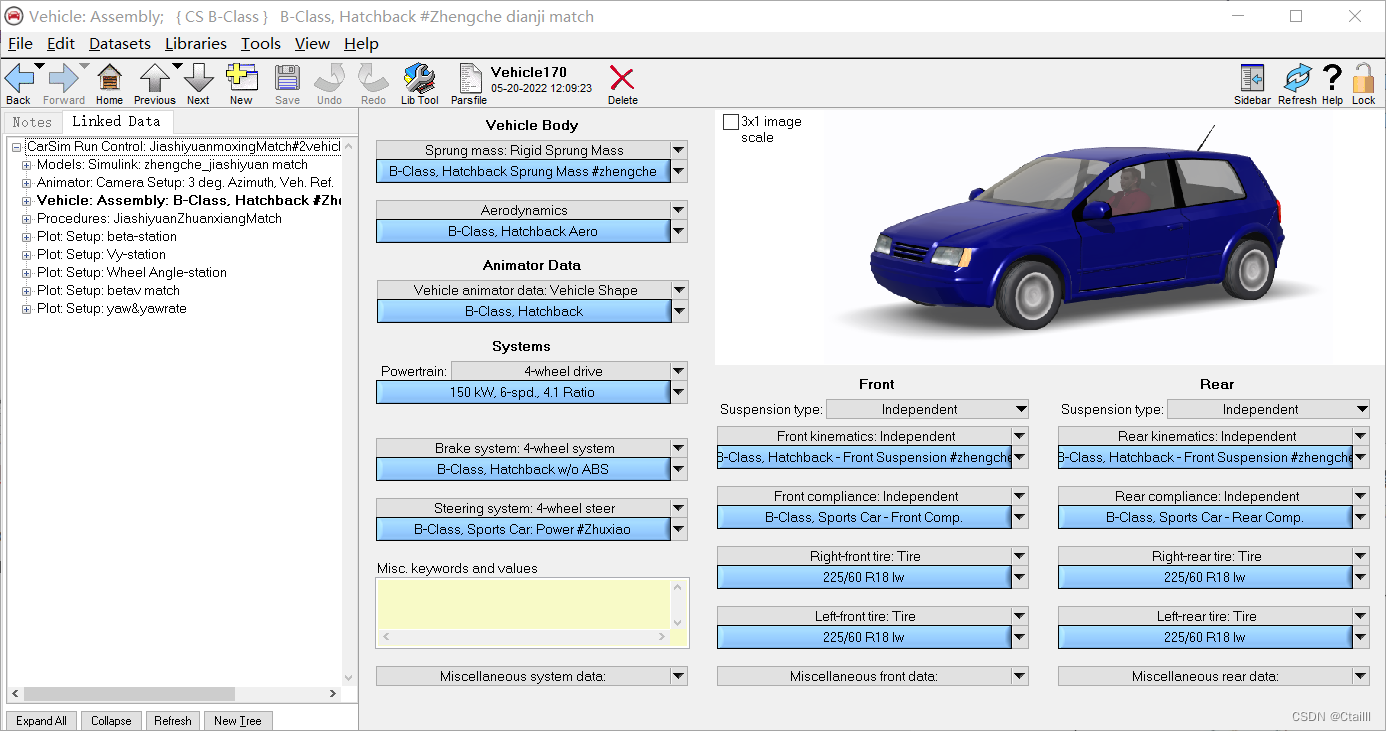
△ 我的更改出于研究对象的参数
Procedure的更改主要是Steering: Drive path follower和车速(由于我研究的是转向性能,故车速设置为Constant target speed)。前者更改内容是目标轨迹,可以选用内置轨迹和驾驶员参数,我是自定义轨迹(在54km/h时,可以满足ISO3888-1-2018 国际标准试验文件),驾驶员参数均为0,如图3-6和3-7所示。 此处需要注意,上述设定需要和Simulink模型对应,如轨迹点和模型中的预期轨迹需一致。

△ Start and Stop time也要改,不同车速对应不同结束时间

△ 也可以直接在内置双移线轨迹的基础上更改,我的双移线参数来自课题组
由于是对照组,只需要想Simulink输出CarSim的数据即可,如图3-8和3-9所示。

△ 其他设定可参照本系列第一篇文章《【整车Silmulink模型】(一)整车动力学模型》

△ 分别为车辆质心纵向车速(单位m/s)、车辆质心侧向车速(单位m/s)和横摆角(单位°)
我运行了一下图3-3所示Simulink模型,输出XY Graph如图3-10所示,可证明上述设定有效。

part1
对于模型组,Simulink便是将注释掉的部分恢复即可,如图3-11所示。由于驾驶员模型需要调参,直接输出纵侧向位移数据至工作区,通过图像对比验证仿真效果。CarSim模型界面如图3-12所示,和对照组相比,Procedure部分的Steering改为no Steer,如图3-13所示。

△ 此时模型与最终模型有所出入,仅为驾驶员模块的过程模型

△ 此处可以直接通过Plot查看与对照组相比的仿真结果
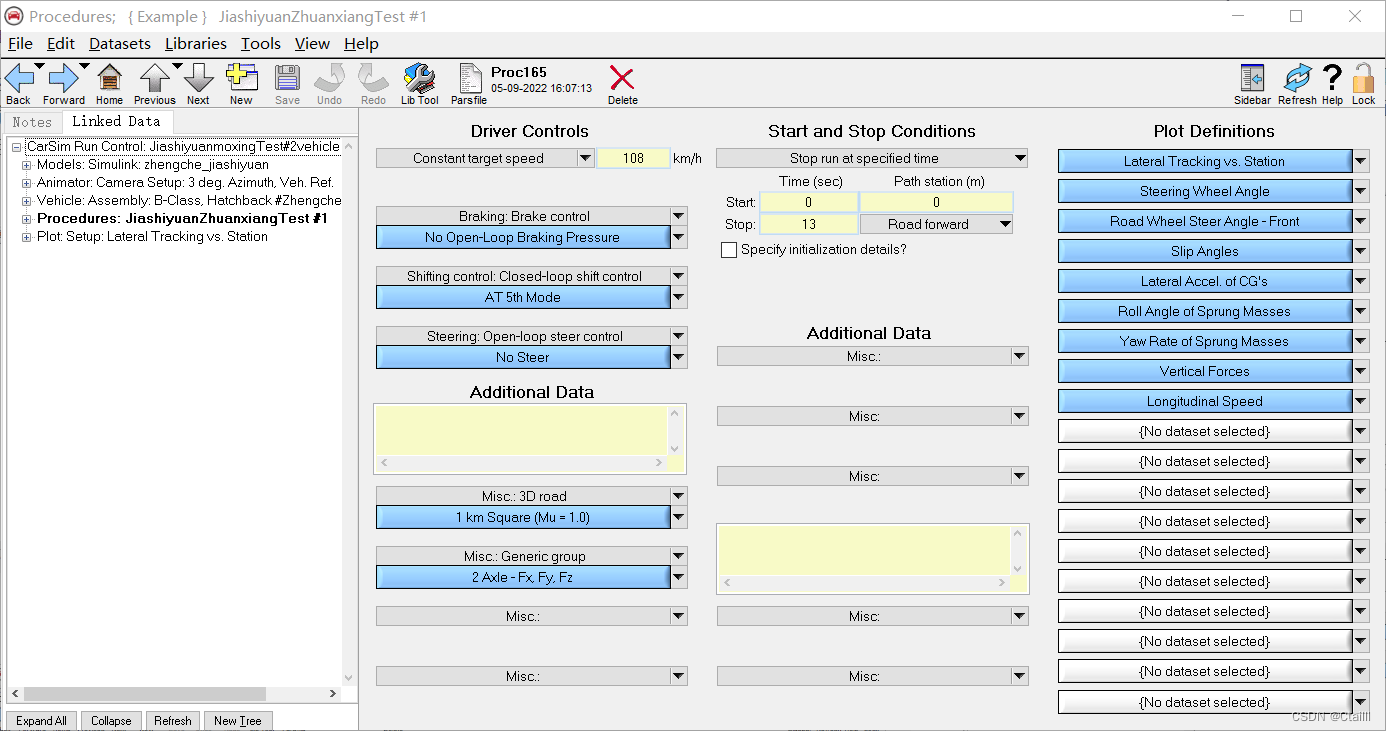
△ 结束时间为13就可以了
联合仿真时,CarSim输出纵侧向车速和横摆角度,输入为方向盘转角,如图3-14-3-16所示。

△ 其他设定可参照本系列第一篇文章《【整车Silmulink模型】(一)整车动力学模型》
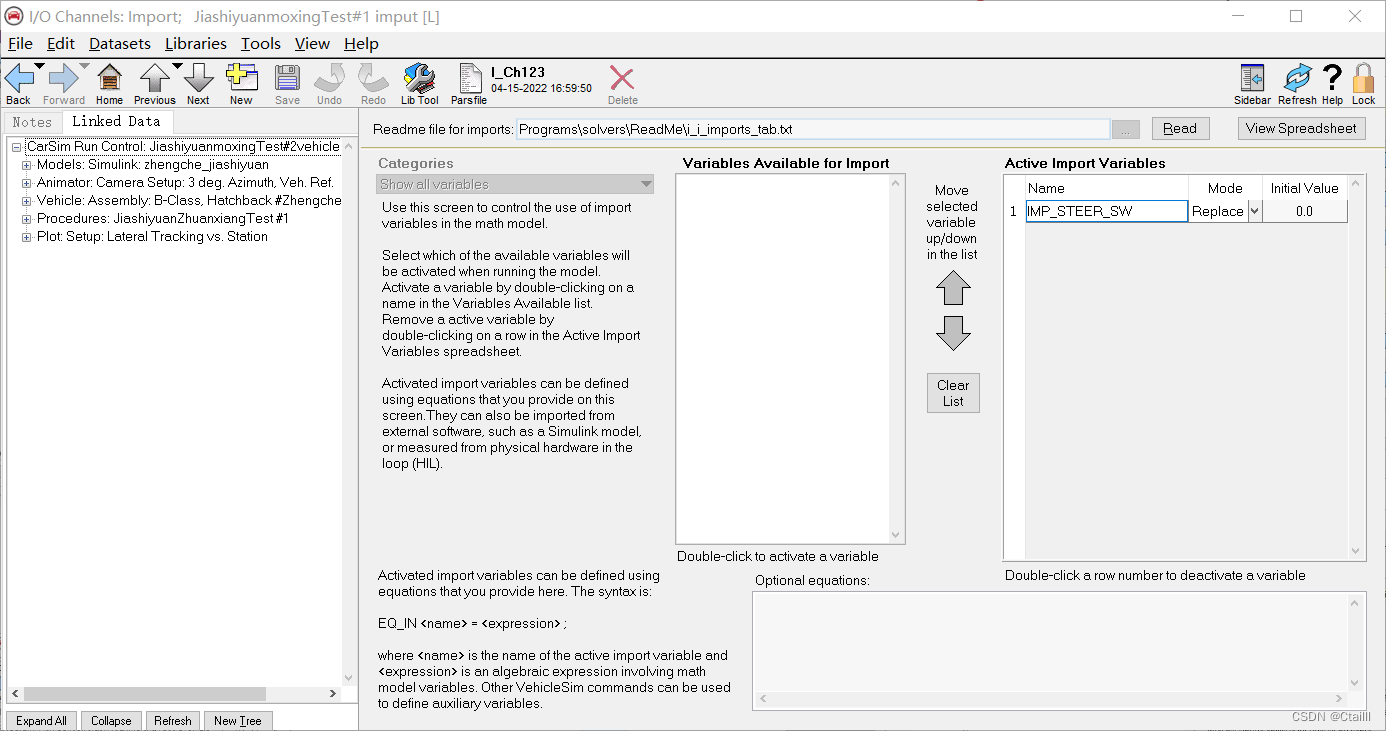
△ 方向盘转角(单位°)

△ 分别为车辆质心纵向车速(单位m/s)、车辆质心侧向车速(单位m/s)和横摆角(单位°)
我运行了一下图3-11所示Simulink模型,输出XY Graph如图3-17所示,可证明上述设定有效。

最终的对比图如图3-18所示,其中,Yobj代表目标轨迹、Y代表Simulink模型的驾驶员轨迹、Ymat代表CarSim的驾驶员轨迹。可以看到,虽然后两者并没有完全重合,但在理论趋势上,两条曲线是一致的。

△ 此为MATLAB输出曲线,过程图像并未加入坐标轴,且速度不一定为108km/h
总结
本文介绍了整车Simulink模型中的驾驶员模型,其中,预期轨迹坐标(或称预瞄点坐标)的获取方法是通过坐标系的变换,而后查表(目标轨迹曲线)获得。本文还阐述了Simulink驾驶员模型与CarSim模型的联合仿真,以验证Simulink模型的有效性。
























 2819
2819

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








