花书——线代and概率论

---

title: 花书——线代and概率论
date: 2024-04-15 13:55:21
categories : Deep Learning
tags:

• Deep Learning
• 花书
• 线性代数
• 概率论
• 信息论
  top: false
  mathjax: true

---

{% cq %} 研读花书，皆为拙记，如有错误还望各位不惜笔墨，不啬赐教。本节主要包括线性代数与概率论部分内容 {% endcq %}

当然，笔者所记不能是花书所有的内容，只能是笔者自己觉得有提升、有意义的部分，所以很多课堂上已经掌握的内容就没有纳入本文的内容了

引言

一些人工智能项目旨在将世界所包含的知识用形式化的语言进行硬编码 (hard-code) ，而计算机可以使用逻辑推理规则自动理解这些形式化语言中的声明。这就是人工智能的知识库 (knowledge base)

依靠硬编码的知识体系面对的困难表明，AI系统需要具备自己获取知识的能力，即从原始数据中提取模式的能力——机器学习 (machine learning) 的能力

对于很多任务来说，我们很难知道应该提取哪些特征，解决这个问题的途径之一就是使用机器学习来发掘表示本身，而不仅仅把表示映射到输出，这种方法称之为表示学习 (representation learning)

一个典型例子是自编码器 (autoencoder)。自编码器由一个编码器 (encoder) 和一个解码器 (decoder) 函数构成。编码器函数将输入数据转为一种不同的表示，而解码器函数则将这个新的表示转换到原来的形式。
而我们的目标是：数据经过编码器和解码器能够尽可能多地保留信息，同时，新的表示有一些好的特性。。。

设计特征或设计用于学习特征的算法时，我们的目标通常是分离出能够解释观察数据的 变差因素 (factors of variation) 。

这些因素可能是现实世界中观察不到的物体或者不可观测的力，但会影响可观测的量
比如分析语音记录时，变差因素包括说话者的年龄、性别等等。。。

深度学习 (deep learning) 通过其他较为简单的表示来表示复杂表达，解决了表示学习中的核心问题

如在图片理解这个任务上，计算机是难以理解以像素集合的图像的
直接处理，让机器学习或评估几乎是不可能的
深度学习将复杂的映射分解为一系列嵌套的简单的映射
输入展示在可见层 (visible layer)，命名的原因是它包含我们能够观察到的变量
然后经过一系列的隐藏层 (hiden layer)

评估模型深度的方式主要有两种：

• 评估计算流深度
• 评估概念关联深度
  • 比如一个AI系统观察到一只眼睛在阴影中的脸部图象时，他可能看到一只眼睛。但是当其检测到脸部的存在后，系统可能推断第二只眼睛也是存在的。这种情况下，概念图包括两层关系（关于眼睛的层和关于脸的层），但如果我们细化每个概念的估计需要额外的 n 次计算，也就是说计算的图包含 2n 层

---

线性代数

在这里，矩阵被看作是列向量集合，即 $A=[{\alpha }_1,{\alpha }_2,{\alpha }_3,\cdots ,{\alpha }_n]$ ，而每个列向量被看作是方向的描述
因此 $Ax={\sum }_i{x}_i{A}_{:,i}$ 可以被描述为我们需要沿着第$i$个向量的方向走$x_i$的步长

一组向量的 生成子空间(span) 是原始向量线性组合后所能抵达的点的集合
也就是说，方程 $Ax=b$是否有解，相当于：确定向量$b$是否在$A$的列向量集合的生成子空间中，这个特殊的生成子空间也被称为 $A$ 的列空间(column space) 或是$A$的值域(range) 。

讨论方程 $Ax=b$ 是否有解？

前提我们记 $A$ 的形状为 $m\times n$

那么一方面，若要求该方程对任意的$b$都要有解，由于$Ax$ 看作是$A$的第$i$个列向量，所以$Ax$自然有$n$个，故若$Ax$的列空间是整个${\mathbb{R}}^m$要求$n\ge m$
（当然，这只是必要条件，这些列向量会存在冗余，这种现象称之为 线性相关 ）

另一方面，如果想要该矩阵可逆，需要使得方程对每一个 $b$ 至多有一个解。

这一句可能有些同学一开始看会愣一下，笔者在这里卡了一下，作者的意思是 $Ax=b$，既然$A$是广义上可逆的，那么 $x=A^{-1}b$ ，也就是说，x是 $A^{-1}$ 的列空间中的一个向量，所以说，x至多也只能有一个，不可能在$A$可逆的情况下一个 $b$ 向量对应多个 $x$ 向量

所以该矩阵需要确保至多有 $m$ 个列，当然，这是个充分条件
综上所述，如果方程有唯一解那么 $A$ 矩阵首先要是方阵，其次他所有的列向量都要是无关的

范数

在机器学习中，我们通过称为 范数 (norm)的函数来衡量向量的大小，形式上 $L^p$范数的定义为：
$$||x|{|}_p={\left(\sum _i|x_i{|}^p\right)}^{\frac{1}{p}}$$
范数能够将向量映射为非负值
直观上来看，向量$x$的范数衡量了从原点到点$x$的距离，更严格地说，范数满足如下性质：

• $f(x)=0\to x=\vec{0}$
• $f(x+y)\le f(x)+f(y)$
• $\forall \alpha \in R,f(\alpha x)=|\alpha |f(x)$

举几个例子吧！

• 当 $p=2$ 时，$L^2$ 范数称为 欧几里得范数(Euclidean norm)：表示从原点出发到向量 $x$ 确定的点的欧几里得距离。通常情况也用 $L^2$ 范数的平方去代替 $L^2$ 范数，不过也有利有弊，一方面，平方在原点附近的增长非常缓慢，另一方面，平方的导数只取决于对应的元素
• 当 $p=1$ 时， $L^1$ 范数却能够给我们区分零元素和非零元素， $L^1$ 范数的计算也非常简单，即各位的绝对值和
• 当 $p=0$ 时，这种 $L^0$ 范数用来统计向量中非零元素的个数，有时我们会用他来衡量一个向量的大小，但这个概念对于前面数学上的严格定义是不对的，首先第三条就不满足了。。。
• 当 $p=+\infty$ 时，也被称为最大范数(max norm)，这个范数表示向量中具有最大幅值的元素的绝对值：$||x|{|}_{\infty }={\max }_i|x_i|$
• 当然，在机器学习中，我们有时也希望有类似的定义能够去衡量矩阵的大小，这要引入 Frobenius范数(Frobenius norm)： $||A|{|}_F=\sqrt{{\sum }_{i,j}{A}_{i,j}^2}$ （类似于向量的 L2 范数？）

特征分解

许多数学对象可以通过将它们分解成多个组成部分或者找到它们的一些属性而更好地理解，这些属性是通用的，而不是由我们选择表示它们的方式产生的。
例如：$12=2×3×3 $，从中我们可以获得一些信息，比如12不能被5整除

通过矩阵的特征分解(eigen decomposition)我们同样能够获得一些信息，方阵 A 的 特征向量（eigen vector）是指与 A 相乘后相当于对该向量进行缩放的非零向量 v：$Av=\lambda v$
其中 $\lambda$ 称为这个特征向量对应的特征值(eigen value)。（类似地，我们也可以定义 左特征向量（left eigen vector）$v^{\top }A=\lambda v^{\top }$，但是通常我们更关注 右特征向量（right eigen vector））。显然，对特征向量缩放后的向量依然是矩阵的特征向量。
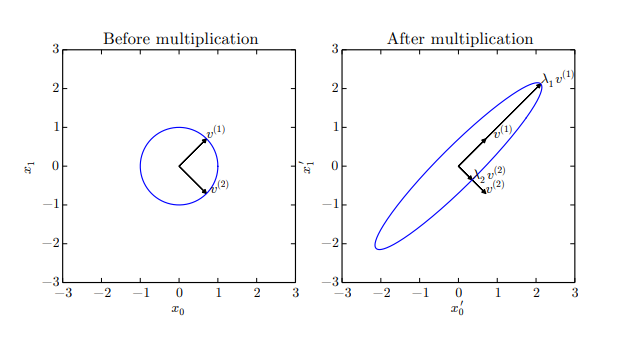
假设矩阵 A 有 n 个线性无关的特征向量 { v ( 1 ) , ⋯   , v ( n ) } \{v^{(1)},\cdots,v^{(n)}\} {v(1),⋯,v(n)} 对应着特征值 { λ ( 1 ) , ⋯   , λ ( n ) } \{\lambda^{(1)},\cdots,\lambda^{(n)}\} {λ(1),⋯,λ(n)} , 因此 A 的特征分解可以记作： $A=V\mathrm{diag}(\lambda ){\mathrm{V}}^{-1}$
不过值得注意的是，并不是所有实矩阵都总有实特征分解，有些特征分解存在但是涉及到复数，不过值得注意的是，所有的实对称阵都可以分解成实特征向量和实特征值：$A=Q\Lambda Q^T$，其中 $Q$ 是 $A$ 的特征向量组成的正交矩阵，$\Lambda$ 是对角矩阵。

奇异值分解

对于非方阵矩阵，我们同样希望能够进行分解，换句话说我们希望将特征分解的范围拓展
这种分解方法被称为 奇异值分解（singular value decomposition, SVD），将矩阵分解为 奇异向量（singular vector）和 奇异值（singular value）
同样地，奇异值分解为：$A=UD{V}^T$
假设 A 是一个 $m\times n$的矩阵,那么U是一个 $m\times m$的矩阵,D是一个$m\times n$的矩阵,V是一个 $n\times n$ 的矩阵
矩阵 U 和 V 都定义为 正交矩阵，而矩阵 D 定义为对角矩阵。注意，矩阵 D 不一定是方阵。
对角矩阵 D 对角线上的元素被称为矩阵 A 的 奇异值（singular value）。矩阵U 的列向量被称为 左奇异向量（left singular vector），矩阵 V 的列向量被称 右奇异向量（right singular vector）。
事实上，我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。A 的 左奇异向量（left singular vector）是 $A{A}^{\top }$ 的特征向量。A 的 右奇异向量（right singular vector）是 $A^{\top }A$ 的特征向量。A 的非零奇异值是 $A^{\top }A$ 特征值的平方根，同时也是$A{A}^{\top }$ 特征值的平方根。
奇异值分解的推导如下：

参考视频

MP伪逆

对于非方阵而言，其逆运算没有定义，因此我们也需要对逆的概念进行拓展
如果矩阵 A 的行数大于列数，那么上述方程可能没有解。如果矩阵 A 的行数小于列数，那么上述矩阵可能有多个解
Moore-Penrose 伪逆（Moore-Penrose pseudoinverse）使我们在这类问题上取得了一定的进展。矩阵 A 的伪逆定义为：$ A ^ { + } = \lim _ { \alpha \to 0 } ( A ^ { T } A + \alpha I ) ^ { - 1 } A ^ { T }$

而计算伪逆通常使用奇异值分解：$ A ^ { + } = V D ^ { + } U ^ { T } $
其中，矩阵 U，D 和 V 是矩阵 A奇异值分解后得到的矩阵。对角矩阵 D 的伪逆$D^{+}$ 是其非零元素取倒数之后再转置得到的。
MP伪逆在方程解的问题中也有很多应用，比如：

• 当 $n>m$ 时，$x=A^{+}y$是所有方程可行解中$L_2$范数最小的那个
• 当 $n>m$​ 时，MP伪逆得到的解使得 $Ax$​ 与 $y$​​ 的欧几里得距离最小

迹运算

迹运算主要集中于以下几点

• $Tr(A)={\sum }_i{A}_{i,i}$
• $Tr(A)=Tr(A^T)$
• $||A|{|}_F=\sqrt{Tr(A{A}^T)}$
• $ Tr ( {\prod _ { i = 1 } ^ { n }} {F ^ { ( i ) }} ) = Tr ( F ^ { ( n ) } {\prod _ { i = 1 } ^ { n - 1 }} {F ^ { ( i ) }} ) $​ (多个矩阵相乘得到的方阵的迹，和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的)

行列式

行列式，记作 det(A)，是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是 0，那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是 1，那么这个转换保持空间体积不变。

主成分分析

主成分分析（principal components analysis, PCA）

---

首先，假设我们有 m 个 n 维的样本 { x 1 , x 2 , ⋯   , x m } , x i ∈ R n \{x_1,x_2, \cdots,x_m\},x_i\in R^n {x1​,x2​,⋯,xm​},xi​∈Rn ，我们希望使用某种压缩，对于每个 $x_i$ 找到对应的 $c_i\in R^l$ ，一般的 $l < n $ ，进行压缩

• 对于编码器 $f(x)=c$
• 对于解码器 $x\approx g(c)=g(f(x))$

为了简化解码函数的选择，我们可以通过矩阵乘法将其映射回 n 维空间，即 $g(c)=Dc$

注意到，当 c 等比例扩大缩小时，D同样等比例缩小扩大，可以得到无数个结果，因此我们限制 D 中的所有列向量都有单位范数

同样，为了让编码问题更简单，PCA限制 D 的列向量彼此正交（D不是严格意义上的正交阵）

我们如何去找到这个 c ，使得他能够被精确解码？这里给出的方法是最小化原始向量 $x$ 与重构向量 $g(c^{\ast })$ 的距离，即 $c^{\ast }={\arg \min }_c||x-g(c)|{|}_2$ ，由于二范数非负性，所以我们可以通过平方进行优化

由于第一项并不依赖于 c ，所以可以再度简化为 $c^{\ast }={\arg \min }_c-2x^{T}g(c)+g(c{)}^{T}g(c)$

带入 $g(c)$ 的定于，以及 $D$ 矩阵的列向量互相正交的一些约定，我们有

$$c^{\ast }={\arg \min }_c-2x^{T}Dc+c^{T}c$$

通过向量微积分，能够推导得到结论：

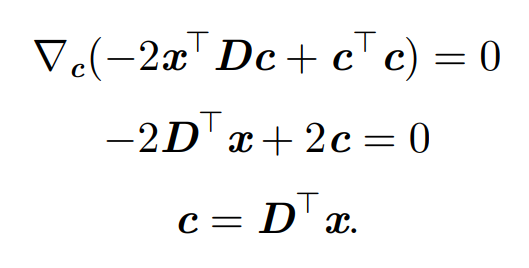
所以推导得到编码函数也就能够写成 $f(x)=D^{T}x$

那么，另一方面该如何选取投影矩阵 D ？

当然这个 D 是作用在全体样本上，与刚刚的思路类似，我们需要使得误差矩阵的 Frobenius 范数最小，也就是 $D^{\ast }={\arg \min }_D\sqrt{{\sum }_{i,j}(x_j^{(i)}-r(x^{(i)}{)}_j{)}^2}\mathrm{subject}\mathrm{to}{D}^{T}D=I_l$
其中 $r(x)=g(f(x))=D{D}^{T}x$

首先考虑一维的情况，问题简化为：

$$d^{\ast }={\arg \min }_d\sqrt{\sum _i(x^{(i)}-d{d}^T{x}^{(i)}{)}^2}\mathrm{subject}\mathrm{to}||d|{|}_2=1$$

由于 $d^{T}x$ 是标量，可以重排位置，参考花书

这里求和号实际上不方便理解，因此我们写成矩阵的形式，重新表述为$$d^{\ast }={\arg \min }_d||X-Xd{d}^T|{|}_F^2\mathrm{subject}\mathrm{to}{d}^{T}d=1$$

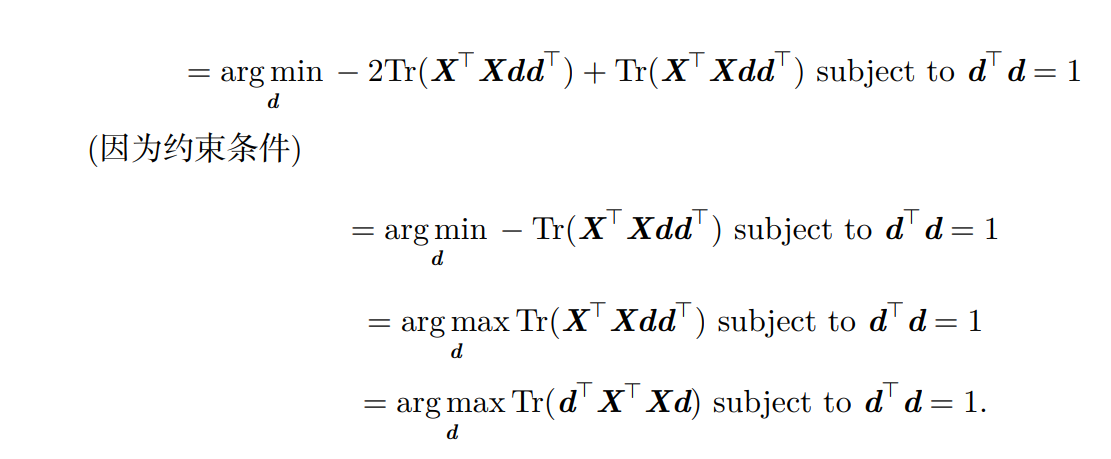
这里将 $X^{T}X$ 处理为对称阵，那么 $y^T{X}^{T}Xy$ 就是一个二次型，那么显然他的最大值应该是最大特征值，对应y向量为对应特征值的特征向量。。。

概率论

不确定信息的来源：

• 被建模系统内在的随机性。这个好理解，比如打扑克，洗牌当然存在一定的随机性
• 不完全观测。这个也好理解，我们没有办法总能够观察到所有驱动系统行为的变量。
• 不完全建模。当我们使用一些必须舍弃某些观测信息的模型时，舍弃的信息会导致模型的预测出现不确定性。

在引入贝叶斯概率后，概率呈现出两种意义：

• 直接与事件发生的概率相联系——频率派概率(frequentist probability)
• 涉及到确定性水平——贝叶斯概率(Bayesian probability)

概率分布

离散型随机变量

离散型变量的概率分布可以用 概率质量函数(probability mass function, PMF) 来描述，通常用大写字母 P 来表示PMF。PMF可以同时作用于多个随机变量，这多个变量的概率分布被称为联合概率分布(joint probability distribution)，如果一个函数是随机变量x的PMF，必须要满足一些条件：

• P定义域为所有x的状态集合
• $\forall x\in \mathrm{x},0\le P(x)\le 1$
• ${\sum }_{x\in \mathrm{x}}P(x)=1$​ ，这条性质称为归一化的(normalized)

连续性随机变量

同理，这里的PMF被描述为概率密度函数**(probability density function，PDF)** ，同样的，他需要满足几个条件：

• p定义域是所有x可能的状态的集合
• $\forall x\in \mathrm{x},p(x)\ge 0$ （！这里不要求 $p(x)\le 1$ 因为一个点处的密度哪怕是非常大，也不一定能够影响总体的概率
• $\int p(x)\mathrm{d}x=1$

概率密度函数 $p(x)$ 并没有直接对特定的状态给出概率，相对的，它给出了落在面积为 $\delta x$ 的无限小的区域内的概率为 $p(x)\delta x$。

边缘概率

若我们知道一组变量的联合概率分布，但只需要了解其中一个子集的分布，那么我们可以如下计算：

• 离散型

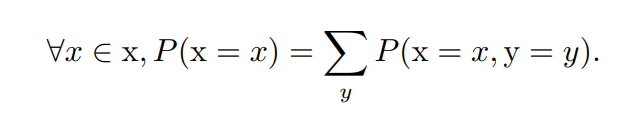
• 连续型

​

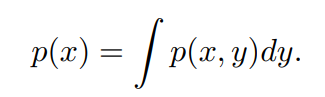
条件概率

条件概率可以通过公式 $P(\mathrm{y}=y|\mathrm{x}=x)=\frac{P(\mathrm{y}=y,\mathrm{x}=x)}{P(\mathrm{x}=x)}$

这里需要注意的是，不要把条件概率和计算当采用某个动作后会发生什么相混淆。假定某个人说德语，那么他是德国人的条件概率是非常高的，但是如果随机选择的一个人会说德语，他的国籍不会因此而改变。计算一个行动的后果被称为 干预查询（intervention query）。干预查询属于 **因果模型（causal modeling）**的范畴

参考了网络上的一些解释，笔者的浅显理解是，调剂概率强调状态而干预查询强调改变

例如$P(销售量|汉堡的价格为20元)$ 与 $P(销售量|降价至20元)$ ，前者是条件概率而后者则是干预查询

独立与条件独立

对于两个随机变量x和y，广义的独立是他们的某种概率可以拆分成互不相关的两个因子的乘积形式，即认为他们是独立的

• 独立：$\forall x\in \mathrm{x},y\in \mathrm{y},p(\mathrm{x}=x,\mathrm{y}=y)=p(\mathrm{x}=x)p(\mathrm{y}=y)$
• 条件独立：$\forall x\in \mathrm{x},y\in \mathrm{x},z\in \mathrm{z},p(\mathrm{x}=x,\mathrm{y}=y|\mathrm{z}=z)=p(\mathrm{x}=x|\mathrm{z}=z)p(\mathrm{y}=y|\mathrm{z}=z)$

可以使用一种较为简单的记号去描述他们的独立性

• x和y相互独立：$x\perp y$
• x和y在给定条件为z时条件独立：$x\perp y|z$

常用概率分布

Bernoulli 分布

伯努利分布是单个二值随机变量的分布。他由单个参数 $\varphi \in [0,1]$ 控制，他具有一些性质：

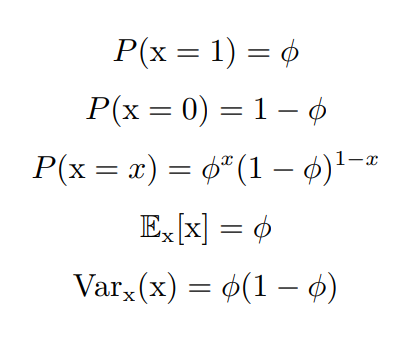
Multinoulli 分布

**Multinoulli 分布（multinoulli distribution） ** 或者 范畴分布（categorical distribution） 是指在具有 k 个不同状态的单个离散型随机变量上的分布，其中 k 是一个有限值

Multinoulli分布由向量 $p\in [0,1{]}^{k-1}$ 参数化，其中每一个分量 $p_i$ 表示第 i 个状态的概率，第 k 个状态可以通过 $1-1^{T}p$ 给出，因此需要加以限制 $1^{T}p\le 1$

高斯分布

实数上最常用的分布就是正态分布（normal distribution），也称为高斯分布 （Gaussian distribution）：

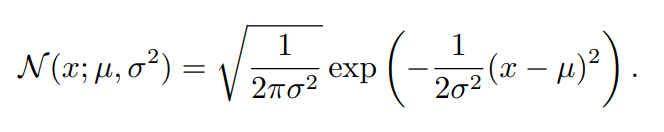
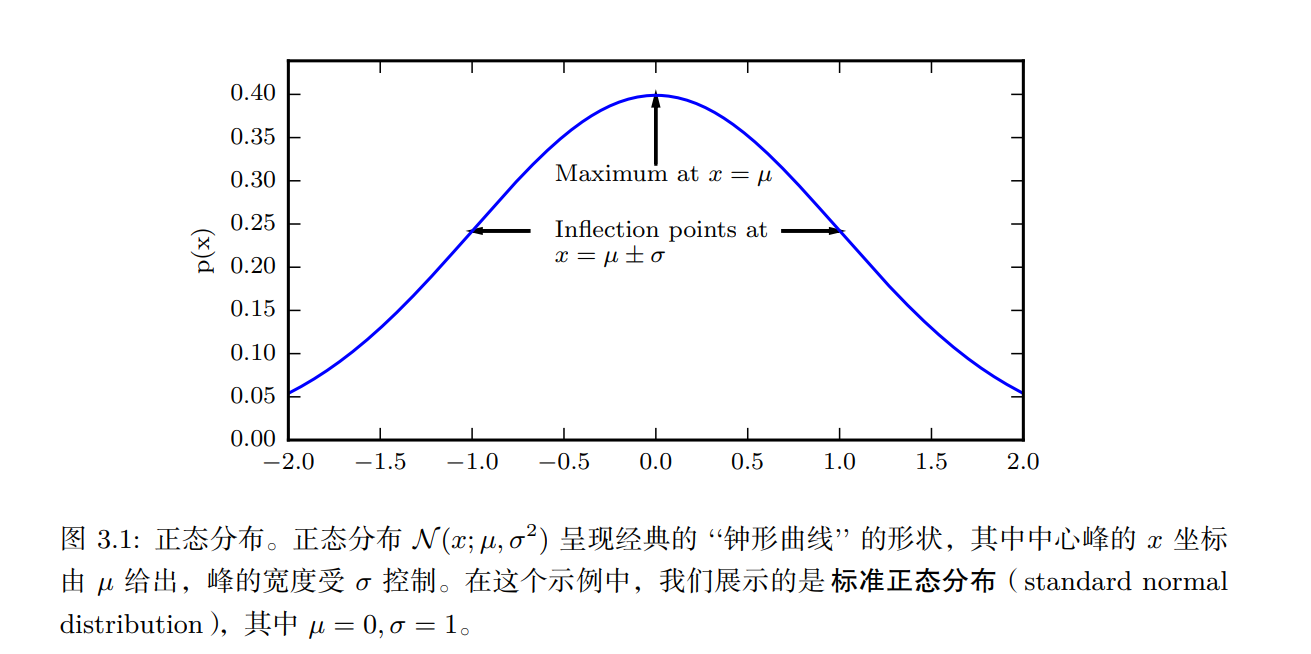
正态分布由两个参数控制，$\mu \in R$ 和 $\sigma \in (0,\infty )$ 。$\mu$ 给出了参数的均值，也是分布的均值，标准差用 $\sigma$ 控制，方差为 ${\sigma }^2$

通常情况下，为了控制正态分布，不会选择直接控制 $\sigma$ 而是控制 $\beta ={\sigma }^{-1}$

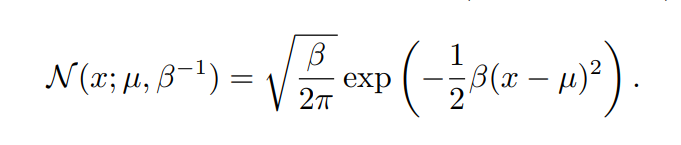
一般地，当缺乏对某个实数上分布的先验知识而不知道怎么选择分布时，正态分布是默认比较好的选择，有两个原因：

• 一方面，根据中心极限定理，很多独立随机变量的和近似服从正态分布。故实际上一些复杂的系统可以被建模成正态分布的噪声
• 另一方面，在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。

同样的，将正态分布推广到高维形式，其参数推广为矩阵化：

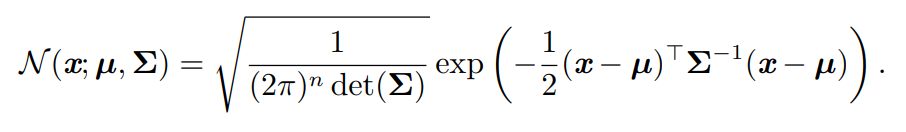
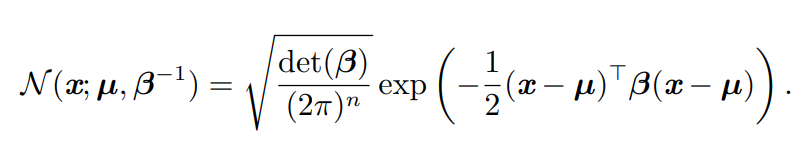
同样我们通过精度阵对概率密度函数进行控制

指数分布与Laplace分布

在深度学习中，我们经常会需要一个在 x = 0 点处取得边界点 (sharp point) 的分布。为了实现这一目的，我们可以使用 指数分布（exponential distribution）：

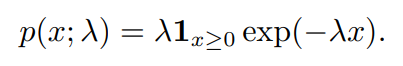
指数分布使用指示函数(indicator function) $1_{x\ge 0}$ 来使得x为负时的值为0

一个与指数分布类似的函数是拉普拉斯分布，它能够控制在任意一点$\mu$ 处设置概率质量的峰值：

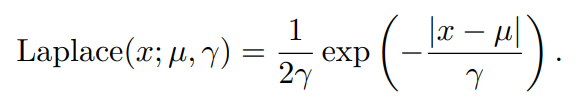
Dirac分布和经验分布

既然拉普拉斯分布可以控制峰值，那么有没有一种分布可以控制将所有的质量集中在一个点处呢？答案是有的，可以通过 Dirac delta函数（Dirac delta function，也称单位脉冲函数） $\delta (x)$ 定义概率密度函数来实现：$p(x)=\delta (x-\mu )$

Dirac delta函数被定义为在除了0以外的所有点的值都为0，但是积分为1，也就是说，他在$\mu$​ 处无限窄也无限高

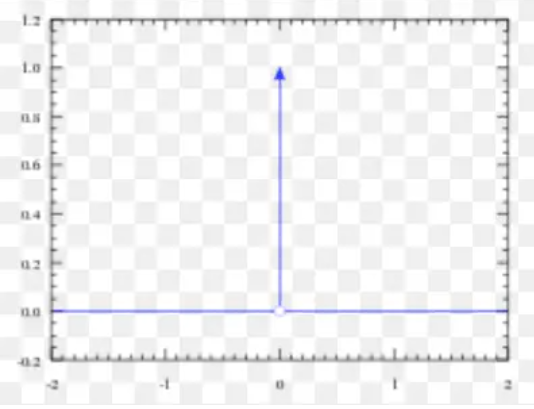
说明:

• 严格来说狄拉克δ函数不能算是一个函数，而是一种数学对象, 因为满足以上条件的函数是不存在的, 但是我们可以用分布的概念来解释, 因此称为狄拉克分布或者δ分布
• 它是一种极简单的广义函数. 广义函数是一种数学对象, 依据积分性质而定义. 我们可以把狄拉克δ函数想成一系列函数的极限点, 这一系列函数把除0以外的所有点的概率密度越变越小

Dirac狄拉克分布经常作为**经验分布（empirical distribution）**的一个组成部分出现：

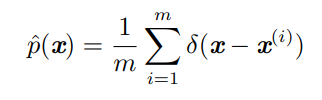
经验分布将概率密度$\frac{1}{m}$​ 赋给m个点，这些点是给定的数据集或者采样的集合。只有在定义连续型随机变量的经验分布时，Dirac delta 函数才是必要的。对于离散型随机变量，情况更加简单：经验分布可以被定义成一个 Multinoulli 分布，对于每一个可能的输入，其概率可以简单地设为在训练集上那个输入值的 经验频率（empirical frequency）。

分布混合

通过组合一些简单的概率分布来定义新的概率分布也是很常见的。一种通用的组合方法是构造 混合分布（mixture distribution）。混合分布由一些组件 (component) 分布构成。

简单来说就是根据范畴分布将一个概率密度集合进行抽样并组合

可以看 [这篇博客](混合分布(mixture distribution)-CSDN博客)

常用函数的有用性质

logistic sigmoid函数作为深度学习中的经典函数：$\sigma (x)=\frac{1}{1+\exp (-x)}$

logistic sigmoid 函数通常用来产生 Bernoulli 分布中的参数 ϕ，因为它的范围是(0, 1)，处在 ϕ 的有效取值范围内。

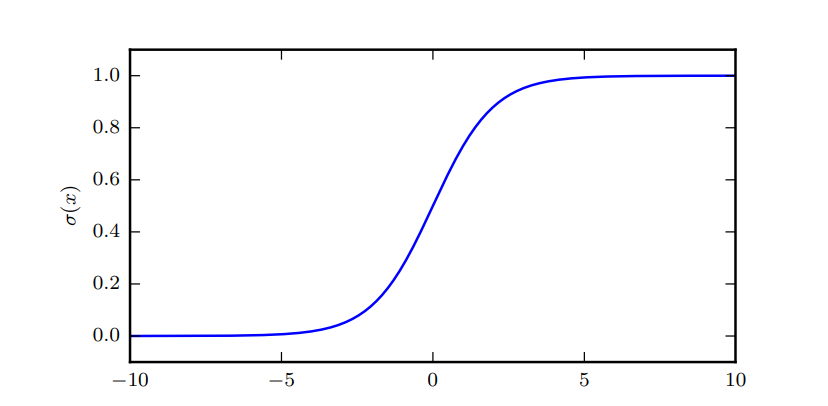
sigmoid 函数 在变量取绝对值非常大的正值或负值时会出现 **饱和（saturate）**现象，意味着函数会 变得很平，并且对输入的微小改变会变得不敏感。

另一个常见函数是 softplus函数：$\zeta (x)=\log (1+\exp (x))$ ,softplus 函数可以用来产生正态分布的 β 和 σ 参数，因为它的范围是 $(0,\infty )$

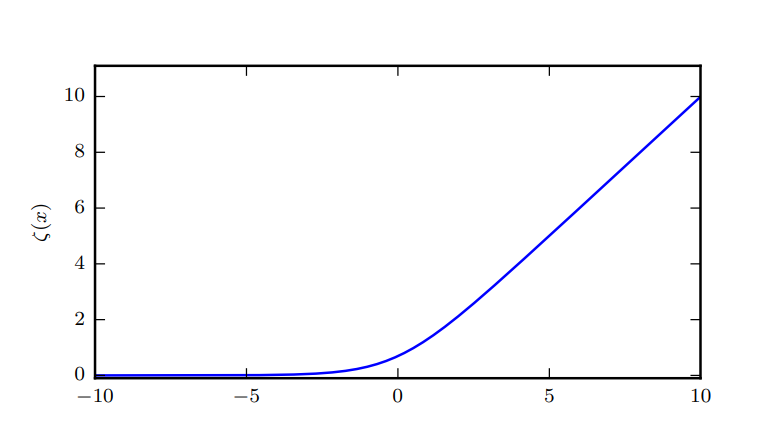
一些有用的性质。。。

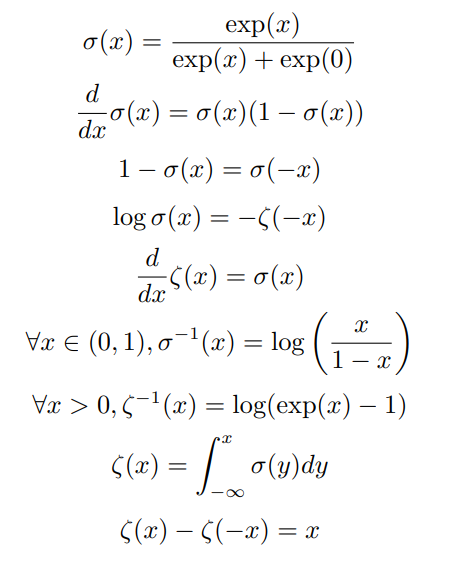
函数 ${\sigma }^{-1}(x)$ 在统计学中被称为 分对数（logit）

贝叶斯规则

通过贝叶斯规则，我们能够在已知 $P(\mathrm{y}|\mathrm{x})$ 时计算 $P(\mathrm{x}|\mathrm{y})$

$P(\mathrm{x}|\mathrm{y})=\frac{P(\mathrm{x})P(\mathrm{y}|\mathrm{x})}{P(\mathrm{y})}$

通常情况下，通过 [全概率公式]([全概率公式_百度百科 (baidu.com)](https://baike.baidu.com/item/全概率公式/9980676#:~:text=若事件A1，A2，…构成一个 完备事件组 且都有正概率，则对任意一个事件B，有如下公式成立： P (B)%3DP (BA1)%2BP (BA2)%2B…%2BP (BAn)%3DP,(B|A2)P (A2) %2B… %2B P (B|An)P (An). 此公式即为全概率公式。) 计算 $P(y)$ 就不需要实现知道 y 的信息了

关于连续性随机变量的一些技术问题

涉及到处理那种相互之间有确定性函数关系 的连续型变量。假设我们有两个随机变量 x 和 y 满足 y = g(x)，其中 g 是可逆的、 连续可微的函数。

可能有人会想 $p_y(y)=p_x(g^{-1}(y))$。但实际上这并不对。

假设我们有两个标量值随机变量 x 和 y，并且满足 y = x/2 以及 x ∼ U(0, 1)。如果我们使用 $p_y(y)=p_x(2y)$，那么 $p_y$ 除了区间 [0, 1/2 ] 以外都为 0，并且在这个区间上的值为 1。这意味着$\int p_y(y)dy=\frac{1}{2}$​

而这违背了概率密度的定义 (积分为 1)。这个常见错误之所以错是因为它没有考虑 到引入函数 g 后造成的空间变形。

我们需要让他在无穷小区域内的概率相同，也就是 $p(x)\delta x$相同

信息论

在机器学习中，我们也可以把信息论应用于连续型变量， 此时某些消息长度的解释不再适用。

信息论的基本想法是一个不太可能的事件居然发生了，要比一个非常可能的事 件发生，能提供更多的信息。

我们想要通过这种基本想法来量化信息。特别地，

• 非常可能发生的事件信息量要比较少，并且极端情况下，确保能够发生的事件 应该没有信息量。
• 较不可能发生的事件具有更高的信息量。
• 独立事件应具有增量的信息。例如，投掷的硬币两次正面朝上传递的信息量， 应该是投掷一次硬币正面朝上的信息量的两倍。

为了满足上述三个性质，我们定义一个事件 x = x 的 自信息（self-information） 为
$$I(x)=-\log P(x)$$

其中 $\log$ 就是以自然对数 e 为底的 ln 函数

我们定义的 I(x) 单 位是 奈特（nats）。一奈特是以 1/e 的概率观测到一个事件时获得的信息量。

亦有教材定义使用底数为 2 的对数，单位是 **比特（bit）**或者 香农（shannons）；通过比特度量的信息只是通过奈特度量信息的常数倍。

我们可以用 **香农熵（Shannon entropy）**来对整个概 率分布中的不确定性总量进行量化：

$H(x)={\mathbb{E}}_{x\sim P}[I(x)]=-{\mathbb{E}}_{x\sim P}[\log P(x)]$ ，也记作 H§。

换言之，一个分布的香农熵是指 遵循这个分布的事件所产生的期望信息总量 。

当 x 是连续的，香农熵被称为 微分熵（differential entropy）

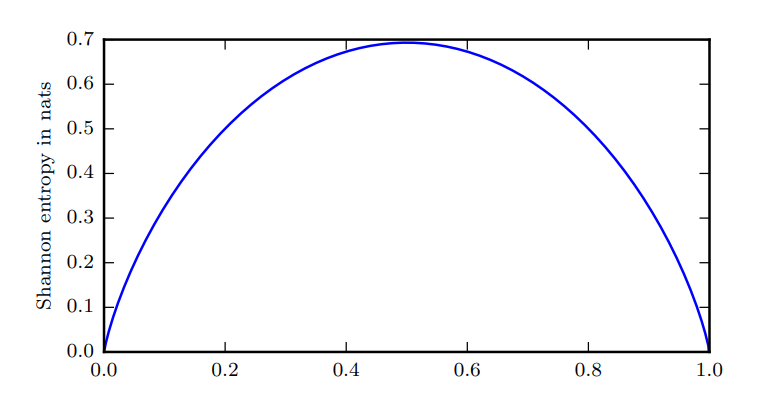
二值随机变量的香农熵。该图说明了更接近确定性的分布是如何具有较低的香农熵，而更 接近均匀分布的分布是如何具有较高的香农熵。水平轴是 p，表示二值随机变量等于 1 的概率。熵由 $(p-1)\log (1-p)-p\log p$ 给出。当 p 接近 0 时，分布几乎是确定的，因为随机变量几乎总是 0。当 p 接近 1 时，分布也几乎是确定的，因为随机变量几乎总是 1。当 p = 0.5 时，熵是最大的， 因为分布在两个结果（0 和 1）上是均匀的。

推导：

二值分布记其随机变量为 x，那么 $p(\mathrm{x}=x)=p^x(1-p{)}^{1-x}$

所以 $H(x)=E(-\log (p^x(1-p{)}^{1-x}))=E(-x\log p+(x-1)\log (1-p))$

由于 $E(x)=p$ ，于是有 $H(x)=(p-1)\log (1-p)-p\log p$

对于同一个随机变量 x 有两个单独的概率分布 $P(x)$ 和 $Q(x)$​ ，使用 KL 散度（Kullback-Leibler (KL) divergence） 来衡量这两个分布的差异：

$$D_{KL}(P||Q)={\mathbb{E}}_{x\sim P}[\log \frac{P(x)}{Q(x)}]={\mathbb{E}}_{x\sim P}[\log P(x)-\log Q(x)]$$

KL散度衡量的是，当我们使用一种编码，这种编码能够使得概率分布Q产生的消息程度最短，在使用这种编码发送一种由概率分布P产生的消息时，所产生的额外信息

KL 散度有很多有用的性质，最重要的是它是非负的。KL 散度为 0 当且仅当 P 和 Q 在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是 ‘‘几乎 处处’’ 相同的。

因为 KL 散度是非负的并且衡量的是两个分布之间的差异，它经常 被用作分布之间的某种距离。 然而，它并不是真的距离因为它不是对称的：对于某 些 P 和 Q，$D_{KL}(P||Q)\ne D_{KL}(Q||P)$ 。这种非对称性意味着选择 $D_{KL}(P||Q)$ 还是$D_{KL}(Q||P)$影响很大。

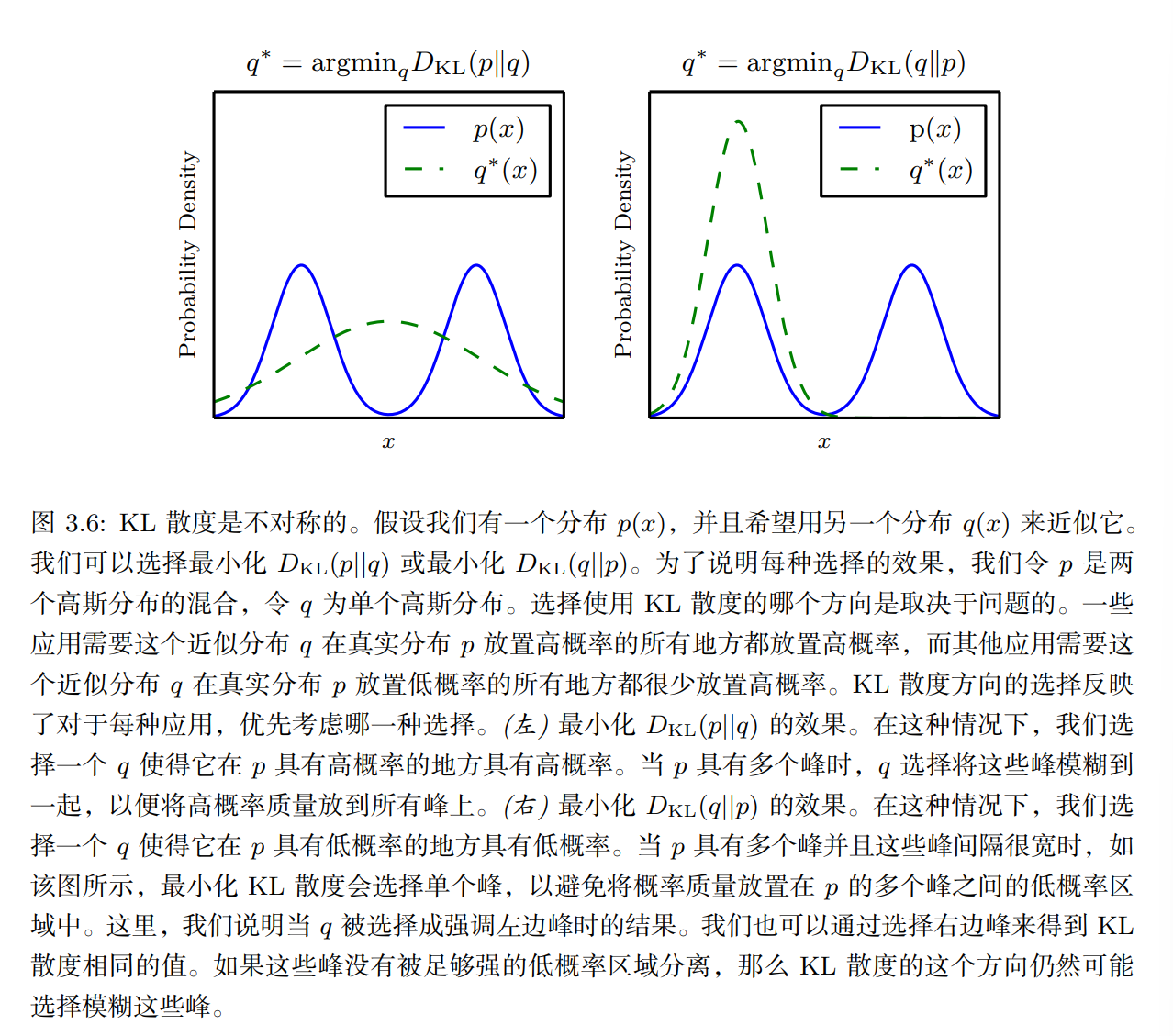
!!!一个和 KL 散度密切联系的量是 交叉熵（cross-entropy）$H(P,Q)=H(P)+D_{KL}(P||Q)$，它和 KL 散度很像但是缺少左边一项：

$$H(P,Q)=-{\mathbb{E}}_{x\sim P}\log Q(x)$$

针对 Q 最小化交叉熵等价于最小化 KL 散度，因为 Q 并不参与被省略的那一项。

在信息论的计算过程中，经常会遇到 $0\log 0$ 的表达式，按照惯例，将它处理成 ${\lim }_{x\to 0}x\log x=0$