【机器学习chp10】降维——(核化)PCA + MDS + lsomap + 拉普拉斯特征映射 + t-NSE + UMAP

信息保留：降维的目标之一是保留原始数据中的“重要”信息，通常是指数据的分布、变异性或结构。不同的降维方法会根据不同的标准来选择保留的信息。
数据压缩：降维也是一种数据压缩方法。通过减少维度，数据的表达更加简洁，同时尽量减少原始数据中的失真。压缩后，数据虽然维度较低，但在某些任务中仍然能够有效地表达数据的内在特征。

3、常见降维方法

降维方法可以分为线性和非线性两类。

（1）线性降维

主成分分析（PCA，Principal Component Analysis）：PCA是最经典的线性降维方法。它通过计算数据的协方差矩阵，提取出数据中的主要成分（主成分），从而将数据投影到一个新的正交坐标系中。PCA的目标是保留数据的最大方差，从而保持数据的主要结构信息。
线性判别分析（LDA，Linear Discriminant Analysis）：LDA是一种监督学习中的降维方法，旨在通过最大化类间散度与类内散度之比来找出最优的低维投影。LDA主要用于分类问题，适用于特征空间维度较高且样本数相对较少的情形。

（2）非线性降维

t-SNE（t-Distributed Stochastic Neighbor Embedding）：t-SNE是一种非线性降维方法，特别适用于高维数据的可视化。t-SNE通过保留数据点之间的局部结构，能有效地将高维数据映射到二维或三维空间，并能展现出数据的潜在聚类或类别结构。
Isomap：Isomap是一种基于流形学习的降维方法，它通过保持数据点之间的全局几何关系，来有效地降低数据的维度。Isomap假设数据可以被嵌入到一个低维的流形上，能够捕捉到高维数据中的非线性结构。

二、基于重构的降维

1、PCA

在本系列【chp4】中已有详细推导分析。

2、核化PCA

（1）实现过程

步骤一：数据映射与核函数定义

数据映射
给定原始数据集
$\{x_1, x_2, \dots, x_N\} \subset \mathbb{R}^d$
我们引入非线性映射
$\phi: \mathbb{R}^d \to \mathcal{F}$
将数据映射到高维（或无限维）的特征空间 $\mathcal{F}$ 。
核函数
定义核函数为映射后的内积
$k(x, y) = \langle \phi(x), \phi(y) \rangle$
例如，对于径向基函数（RBF）核有
$k(x,y) = \exp\left(-\frac{\|x-y\|^2}{2\sigma^2}\right)$

步骤二：构造核矩阵与中心化

核矩阵构造
利用核函数计算所有样本点间的相似度，构造核矩阵 $K$ ：
$K_{ij} = k(x_i, x_j),\quad i,j=1,\dots,N$
数据中心化
为了使映射后的数据均值为零（类似于传统PCA的中心化处理），我们对核矩阵进行中心化。令
$\mathbf{1}_N = \frac{1}{N}\mathbf{1}$
其中 $\mathbf{1}$ 为全1矩阵，则中心化后的核矩阵为
$\tilde{K} = K - \mathbf{1}_N K - K \mathbf{1}_N + \mathbf{1}_N K \mathbf{1}_N$

步骤三：求解特征值问题

在特征空间中，原始PCA要解决协方差矩阵的特征值问题，而在核PCA中，我们通过核矩阵来间接完成这一过程。具体步骤如下：

特征值分解
求解中心化核矩阵的特征值问题：
$\tilde{K}\,\alpha = N\lambda\,\alpha$
其中 $\alpha$ 为特征向量， $\lambda$ 为对应的特征值。注意到这里的 $N$ 为归一化因子。
选择主成分
按照特征值从大到小的顺序，选择前 $m$ 个特征向量和特征值，作为降维时保留的主成分。

步骤四：数据投影到低维空间

主成分的表示
在特征空间中，第 $k$ 个主成分方向可以表示为
$v_k = \sum_{i=1}^N \alpha_{ki}\,(\phi(x_i)-\bar{\phi})$
其中 $\bar{\phi} = \frac{1}{N}\sum_{i=1}^{N}\phi(x_i)$ 为均值。
新样本投影
对于新的数据点 $x$ ，其在第 $k$ 个主成分方向上的投影为
$\langle v_k, \phi(x)-\bar{\phi} \rangle = \sum_{i=1}^N \alpha_{ki}\,\langle \phi(x_i)-\bar{\phi},\phi(x) \rangle$
利用核函数可以将上式写成
$\langle v_k, \phi(x)-\bar{\phi} \rangle = \sum_{i=1}^N \alpha_{ki} \Bigl( k(x_i,x) - \frac{1}{N}\sum_{j=1}^N k(x_j,x) \Bigr)$
这样，新样本xxx就被映射到由选取的mmm个主成分构成的低维空间中，其低维表示为
$y = \Bigl( \langle v_1, \phi(x)-\bar{\phi} \rangle,\, \langle v_2, \phi(x)-\bar{\phi} \rangle,\, \dots,\, \langle v_m, \phi(x)-\bar{\phi} \rangle \Bigr)$

步骤五：总结

核PCA实现降维的数学步骤如下：

数据映射：利用非线性函数 $\phi$ 将原始数据映射到高维特征空间。
构造核矩阵：通过核函数 $k(x,y)=\langle \phi(x),\phi(y)\rangle$ 构造 $K$ 。
中心化：利用公式 $\tilde{K} = K - \mathbf{1}_N K - K \mathbf{1}_N + \mathbf{1}_N K \mathbf{1}_N$ , 对核矩阵进行中心化处理。
特征值分解：求解 $\tilde{K}\,\alpha = N\lambda\,\alpha$ ，获得特征向量和特征值。
数据投影：利用特征向量，将新数据点通过核函数投影到低维空间，实现降维表示。

这种方法既避免了显式计算高维映射，又能利用数据的内在非线性结构，为后续的分类、聚类、可视化等任务提供低维且富含信息的表示。

（2）核PCA的能量来源

对标题的解释：核PCA如何利用数据自身的结构来“适应”问题，以及如何调节大量自由度。

对于SVM，虽然它引入了核函数，但它还有迭代过程来实现一些权重参数与核函数的适应，使得模型的很多自由度得到相匹配，最终实现目标。但是核化PCA并没有其他参数，他是如何实现它适应大多数问题的呢，非常多的自由度是如何调节的呢？此部分就是来解决这个问题。

2.1 核PCA的非迭代“训练”过程

闭式求解
核PCA的核心在于构造并中心化核矩阵，然后对该矩阵做特征值分解。这个过程是一个闭式解，不需要迭代更新参数。
- 核矩阵构造：利用核函数（例如RBF核）计算训练样本之间的相似度，形成一个 N×N 的矩阵。
- 中心化与特征分解：对核矩阵进行中心化后，通过求解特征值问题获得主成分方向。
数据决定模型
在核PCA中，映射到高维空间的方式完全由选择的核函数及其参数（如RBF中的 σ）决定；而一旦核函数和参数确定，模型就通过数据自身构造的核矩阵来捕捉数据的变异结构。
这种“自适应”是由数据在核空间中呈现的内在相似度结构直接决定的，而不是通过外部目标函数反复优化得到的。

2.2 自由度与灵活性如何体现

隐含高维特征空间
核函数（例如RBF核）隐式地将数据映射到一个可能是无限维的空间，使得在这个空间中数据的非线性结构有可能转化为线性关系。
这里的“自由度”主要体现在映射后的空间维度上，但实际上，核PCA的实际自由度受到样本数 N 的限制（核矩阵的秩至多为 N）。
核参数的选择
虽然核PCA没有额外的迭代参数更新过程，但核函数的参数（例如RBF核的 σ）起到了调节映射“灵活性”的作用：
- 较小的 σ 会使得核函数局部化，仅捕捉非常局部的结构，可能导致过拟合局部噪声。
- 较大的 σ 则使得映射更平滑，捕捉全局结构，但可能丢失局部细节。
  通过适当调节这些参数，可以控制映射后的数据结构，使其更好地反映数据本身的变异性。
特征值分解的内在调节
当对中心化后的核矩阵进行特征值分解时，得到的特征值及对应特征向量反映了数据在核空间中的主变异方向。
- 特征值大小排序：最大的特征值对应的方向表示数据在该方向上的变异性最大，选择保留多少个主成分实际上是在调节模型所捕捉的信息量。
- 自由度的限制：虽然核映射空间理论上自由度非常高，但实际中只有那些由数据内在结构决定的、具有显著特征值的方向才被保留下来，起到了自动“调节”高维自由度的作用。

2.3 SVM的迭代优化

SVM的迭代过程
SVM在使用核函数时，需要通过迭代优化（例如求解二次规划问题）来调整支持向量的权重，从而达到最优的分类决策面。
- 这种过程使得模型能在大量自由度中找到最能区分不同类别的方向，并且不断修正权重以适应数据分布。
核PCA的“自适应”机制
核PCA没有目标函数和权重更新，而是通过一开始构造的核矩阵“捕捉”了数据的整体相似度结构。
- 数据在核空间中的内在结构（由核函数决定）和特征值分解过程中自然选取的重要方向，共同构成了对数据非线性结构的描述。
- 因此，即便没有迭代过程，核PCA依然能“适应”大多数问题，因为它直接反映了数据在高维空间中的分布特征，而这些特征本身就是从数据中“学习”出来的。

2.4 总结

核PCA适应问题的关键在于：

通过选择合适的核函数及其参数来隐式构造高维特征空间，使得数据的非线性结构在该空间中展现为线性变异模式；
利用数据构造的核矩阵进行特征值分解，从而自动提取最具代表性的主成分；
自由度的调节主要依赖于核函数参数和选取的主成分数目，而不需要像SVM那样通过迭代优化来调整权重。
普通PCA的协方差矩阵的元素是通过点积（欧氏距离）来表示样本与样本之间的相似度，核化PCA的协方差矩阵的元素代表的是映射到高维空间后的样本与样本之间的相似度（更高维度的距离）。

因此，核PCA尽管没有类似SVM那样的迭代过程，但它通过数据驱动的特征值分解和核函数的灵活设计，仍然能够适应大多数实际问题，捕捉数据中复杂的非线性结构。

3、自编码器（神经网络部分）

到神经网络部分再学习。

三、基于全局结构保持的降维

1、多维缩放MDS

多维缩放（Multidimensional Scaling, MDS）是一种常用的降维和数据可视化技术，其主要目标是：

给定一组对象之间的两两“不相似性”（或距离）数据（原高维空间），通过寻找低维空间中的点配置，使得点与点之间的欧氏距离尽可能反映原始的不相似性。

下面我们从数学推导、算法实现以及本质理解三个方面来详细分析 MDS。

（1）问题定义

假设我们有 n 个对象，且已知它们之间的成对距离（或不相似性） $\delta_{ij}$ （一般认为这些距离满足对称性和非负性）。目标是在 $\mathbb{R}^p$ （其中 $p \ll n$ ）中找出一个点集 $\{ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n \}$ ，使得低维空间中的欧氏距离

$d_{ij} = \|\mathbf{x}_i - \mathbf{x}_j\|$

尽可能接近原始距离 $\delta_{ij}$ 。

（2）传统 MDS 的数学推导

步骤一、距离与内积的关系

设在低维空间中，每个对象的表示为 ${x}_i \in \mathbb{R}^p$ 。两个点之间的欧氏距离的平方有如下表达：

$d_{ij}^2 = (\mathbf{x}_i - \mathbf{x}_j)^\top (\mathbf{x}_i - \mathbf{x}_j) = \mathbf{x}_i^\top \mathbf{x}_i + \mathbf{x}_j^\top \mathbf{x}_j - 2\,\mathbf{x}_i^\top \mathbf{x}_j$

定义格拉姆矩阵（内积矩阵） B 为

$B_{ij} = \mathbf{x}_i^\top \mathbf{x}_j$

则上式可以写成：

$d_{ij}^2 = B_{ii} + B_{jj} - 2B_{ij}$

步骤二、双重中心化（Double Centering）

在 MDS 中，我们通常假设数据已经中心化，即

$\sum_{i=1}^n \mathbf{x}_i = \mathbf{0}$

在这种假设下，可以利用距离矩阵构造内积矩阵。设 $D^{(2)}$ 为距离矩阵的平方，即 $(D^{(2)})_{ij} = d_{ij}^2$ 。引入中心化矩阵

$J = I - \frac{1}{n}\mathbf{1}\mathbf{1}^\top$

其中 $I$ 是 n×n 的单位矩阵， $\mathbf{1}$ 是全1向量。则有公式：

$B = -\frac{1}{2} J D^{(2)} J$

推导思路：

先注意到 B 的对角线元素 $B_{ii} = \|\mathbf{x}_i\|^2$ ；
通过将 $D^{(2)}$ 关于行和列都进行中心化（即消去每个对象的均值影响），可以“恢复”出对象之间的内积关系；
最终得到上式，其中双重中心化确保了所恢复的 B 是关于中心化数据的内积矩阵。

步骤三、特征值分解及低维嵌入

有了内积矩阵 B 后，我们对其做特征值分解：

$B = V \Lambda V^\top$

其中 $\Lambda = \mathrm{diag}(\lambda_1, \lambda_2, \ldots, \lambda_n)$ 是特征值矩阵（通常要求 $\lambda_i \ge 0$ ），而 V 的每一列是对应的特征向量。
由于 B 本质上是 $X X^\top$ （X 为配置矩阵），可以写出：

$X = V \Lambda^{1/2}$

或者只保留最大的 p 个正特征值及对应特征向量构成 $X_p$ ，从而得到 p 维的低维嵌入。

小结

输入：对象间的距离矩阵 D（或其平方 $D^{(2)}$ ）；
核心步骤：通过双重中心化得到内积矩阵 $B = -\frac{1}{2}J D^{(2)} J$ ；对 B 进行特征分解，并用正特征值的平方根和对应特征向量重构低维配置。
结果：低维配置 X 中任意两点的欧氏距离尽量还原原始距离 $\delta_{ij}$ 。

（3）非度量 MDS 的数学原理与算法

在某些应用中，我们并不关心原始距离的精确数值，而更关注距离之间的排序关系。非度量（Non-metric）MDS 的目标是保持原始距离的相对顺序。

3.1 目标函数（Stress Function）

常用的目标函数称为“stress”，例如：

$\text{Stress} = \sqrt{ \frac{\sum_{i<j} \left(f(d_{ij}) - \delta_{ij}\right)^2}{\sum_{i<j} \delta_{ij}^2} }$

其中：

$d_{ij}$ 是低维空间中点之间的欧氏距离；
$\delta_{ij}$ 是原始不相似性；
$f$ 是一个单调递增的函数，用于调整 $d_{ij}$ 与 $\delta_{ij}$ 之间的尺度关系。

目标是寻找一个嵌入 $\{\mathbf{x}_i\}$ 以及合适的 $f$ ，使得 stress 最小。由于 $f$ 只要求保持单调关系，非度量 MDS 主要关注距离顺序而非精确数值。

3.2 优化算法

非度量 MDS 通常采用迭代优化算法来最小化 stress。一个著名的算法是 SMACOF (Scaling by MAjorizing a COmplicated Function)：

主要思想：构造一个上界函数，使得每次迭代能够保证 stress 单调下降；
步骤：先固定 $f$ （通常通过单调回归获得），再更新低维点配置，交替进行直至收敛。

（4）MDS 本质分析

保距离嵌入
MDS 的核心目标是寻找一个低维配置，使得低维欧氏距离尽可能接近原始数据中的距离。对于经典 MDS，假设原始距离实际上源自欧氏空间，那么经过双重中心化和特征分解，可以完美重构这种内积结构；
非度量 MDS 则侧重于“秩”或顺序信息，适用于那些距离只反映相对关系的情形。
与 PCA 的关系
当原始距离为欧氏距离时，经典 MDS 与主成分分析（PCA）具有紧密联系：两者都是基于数据的协方差结构（或内积矩阵）的谱分解。实际上，经典 MDS 只是通过距离矩阵间接恢复出数据的协方差矩阵，再利用 PCA 得到低维表示。
数据可视化与降维
MDS 特别适用于高维数据的可视化。通过在低维（通常是二维或三维）空间中展示数据间的相对关系，可以直观地反映数据的群聚结构、离群点等特性。
假设与局限性
- 假设：经典 MDS 假设原始距离是由欧氏距离引起的，并且数据已经中心化；非度量 MDS 假设距离的排序关系比具体数值更为重要。
- 局限：当原始距离不满足欧氏性质（如非对称距离或非度量数据）时，经典 MDS 可能不适用，此时需要考虑其他降维技术或对距离进行适当变换。

2、Isomap

ISOMAP（Isometric Mapping）是一种经典的流形学习方法，其核心思想是通过保持数据在流形上的测地距离（geodesic distance），将高维数据嵌入到低维空间中。下面我们从算法步骤、详细的数学推导以及本质分析三个方面展开详细讲解。

对于流形，为什么要使用测地距离而不是欧氏距离？

对于流形，如上图中的 Swiss-Roll ，最上面的粉红色的点，它与绿色的点的欧氏距离很近，但从整体流行来看，他们的距离又很远，所以对于流形，欧氏距离具有一定的局限性，所以这里使用测地距离。

（1）问题背景与算法步骤

假设我们有 n 个数据点 $\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_n \in \mathbb{R}^D$ ，这些点位于某个低维流形上（内蕴维数 d，通常 d≪D）。ISOMAP的目标是找到低维表示 $\mathbf{y}_1, \mathbf{y}_2, \dots, \mathbf{y}_n \in \mathbb{R}^p$ （一般 p≈d），使得这些点之间的距离能够较好地反映原始数据点在流形上的测地距离。

ISOMAP主要包含以下三个步骤：

构造邻域图
根据高维空间中的欧氏距离，确定每个点的局部邻域（常用方法有：k近邻或者 ϵ 邻域），构造加权图，其中图的节点为数据点，相邻节点之间的边权为它们之间的欧氏距离。
计算图中最短路径距离
在构造好的邻域图上，利用最短路径算法（如Dijkstra算法或Floyd–Warshall算法）计算任意两点之间的最短路径距离。这些最短路径距离近似地反映了数据在流形上的测地距离，记为 $d_{ij}^G$ 。
经典MDS（Multidimensional Scaling）
将上一步得到的距离矩阵 $D^G = (d_{ij}^G)$ 作为输入，利用经典MDS方法恢复低维嵌入。具体来说，通过双重中心化将距离矩阵转换为内积矩阵，再进行特征值分解，从而得到低维坐标。

（2）数学推导

ISOMAP 的数学推导可以分为两部分：

部分一：近似测地距离的求解
部分二：经典MDS的应用

2.1 构造邻域图与最短路径距离

i、构造邻域图

邻域判定：
给定数据点和在高维空间中的欧氏距离 , 我们可以采用以下两种方式构造邻域关系：
- k近邻：对每个点 $\mathbf{x}_i$ ，选择距离其最近的 k 个点建立边。
- ϵ 邻域：若 $d_{ij} < \epsilon$ ，则在 $\mathbf{x}_i$ 与 $\mathbf{x}_j$ 之间建立边。
加权图的构造：
构造图 G 时，如果两点满足邻域条件，则令边权为 $w_{ij} = d_{ij}$ ，否则令 $w_{ij} = +\infty$ （或视为不存在该边）。

ii、计算最短路径距离

在图 G 中，记任意两点之间的最短路径距离为 $d_{ij}^G$ 。利用标准最短路径算法（如Dijkstra算法），我们可以得到完整的距离矩阵

$D^G = \{d_{ij}^G\}_{i,j=1}^n$

这一矩阵近似反映了原始数据点在流形上的测地距离。

2.2 经典MDS部分的数学推导

经典MDS的基本思想是：给定距离矩阵（这里是 $D^G$ ），构造一个低维配置，使得低维空间中点与点之间的欧氏距离与输入的距离尽可能匹配。这里我们简要回顾经典MDS的关键推导步骤。

i、距离与内积的关系

设低维嵌入中数据点为 $\mathbf{y}_1, \mathbf{y}_2, \dots, \mathbf{y}_n \in \mathbb{R}^p$ ，构成矩阵 $Y \in \mathbb{R}^{n \times p}$ 。令内积矩阵为

$B = YY^\top, \quad B_{ij} = \mathbf{y}_i^\top \mathbf{y}_j$

则任意两点之间的欧氏距离平方为

$\|\mathbf{y}_i - \mathbf{y}_j\|^2 = B_{ii} + B_{jj} - 2B_{ij}$

ii、双重中心化

假设低维嵌入已经中心化（即 $\sum_{i=1}^n \mathbf{y}_i = 0$ ），定义中心化矩阵

$J = I - \frac{1}{n}\mathbf{1}\mathbf{1}^\top$

令 $(D^G)^2$ 表示元素平方后的距离矩阵，其 ijijij 元素为 $(d_{ij}^G)^2$ 。经典MDS证明，通过下面的公式可以恢复出内积矩阵 B：

$B = -\frac{1}{2} J (D^G)^2 J$

详细推导过程与之前MDS的推导类似，核心思想是利用距离与内积之间的关系，通过对行和列进行中心化消除平移影响，从而恢复出内积矩阵。

iii、特征值分解与低维嵌入

对 B 进行特征分解：

$B = V \Lambda V^\top$

其中 $\Lambda = \mathrm{diag}(\lambda_1, \lambda_2, \dots, \lambda_n)$ （要求 $\lambda_i \ge 0$ ）和对应的特征向量矩阵 V。取最大的 p 个特征值和对应特征向量构成矩阵

$Y = V_p \Lambda_p^{1/2}$

这样得到的 Y 就是最终的低维嵌入，其中

$\|\mathbf{y}_i - \mathbf{y}_j\| \approx d_{ij}^G$

（3）ISOMAP 本质分析

3.1 流形学习视角

非线性降维
传统的降维方法（如PCA、经典MDS）假设数据间的距离满足欧氏结构，而ISOMAP通过构造邻域图和计算图中最短路径距离，近似恢复数据在流形上的测地距离，从而能够处理非线性结构的数据。
保持测地距离
ISOMAP的核心在于保持数据的内蕴几何结构。通过近似测地距离，ISOMAP试图保持数据在流形上的“等距性”（isometry），这意味着低维嵌入中的距离能反映原始流形上的真实距离。
与经典MDS的关系
实际上，ISOMAP可以看作是经典MDS的一个扩展。经典MDS直接在原始欧氏距离上工作，而ISOMAP则先通过邻域图求得近似测地距离，再应用经典MDS，从而适用于更为广泛的非线性情况。

3.2 优点与局限性

优点
- 能够有效揭示高维数据的低维流形结构。
- 保持了数据内在的几何性质，特别适用于存在非线性结构的数据集。
局限性
- 邻域图构造：参数 k（或 ϵ）的选取对结果有较大影响，过小可能导致图不连通，过大则可能破坏局部结构。
- 噪声敏感性：噪声和离群点可能严重影响最短路径距离的计算。
- 计算复杂度：对于大规模数据集，计算所有对之间的最短路径距离和进行特征分解会比较耗时。

（4）总结

ISOMAP 的流程可以总结为：

构造邻域图：基于高维数据的欧氏距离，通过 k近邻或 ϵ 邻域方法构造加权图，捕捉局部结构。
计算测地距离：在图上利用最短路径算法计算任意两点之间的近似测地距离，形成距离矩阵 $D^G$ 。
经典MDS嵌入：将 $D^G$ 的平方矩阵经双重中心化转化为内积矩阵 $B = -\frac{1}{2} J (D^G)^2 J$ ，对 B 进行特征值分解，利用主成分构造低维嵌入。

从本质上看，ISOMAP是一种基于流形假设的非线性降维方法，通过保留数据的测地距离揭示数据的内在几何结构。尽管其在处理非线性结构上具有优势，但在参数选择和噪声处理上也存在挑战。

（5）ISOMAP算法

ISOMAP算法中有两个瓶颈：

四、基于局部结构保持的降维

1、拉普拉斯特征映射（Laplacian Eigenmaps）

Laplacian Eigenmaps 是一种基于局部结构保持思想的非线性降维方法，其核心思想在于：

利用构造数据点之间的局部邻域图得到图的拉普拉斯矩阵，并通过图拉普拉斯矩阵的谱分解获得一个嵌入（把特征值小的特征向量当作低维的维度），使得在低维空间中相近的点仍然保持紧密连接，从而保留原数据的局部几何结构（低频信息）。特征向量可形成一组基：前面的成分变化比较平滑（小特征值），后面的成分变化剧烈（大特征值）。

（1）问题背景与基本思想

在许多高维数据中，数据通常假设服从某个低维流形结构。直接使用线性方法（如 PCA）难以捕获非线性关系，而 Laplacian Eigenmaps 通过以下步骤实现非线性降维：

构造局部邻域图
- 邻域选择：对每个数据点 $\mathbf{x}_i \in \mathbb{R}^D$ ，利用 k 近邻或 ϵ 邻域的方法构造图 G；
- 权重设置：定义权重 $w_{ij}$ 来衡量数据点之间的相似性，得到邻接矩阵 W
利用图的拉普拉斯矩阵构造目标函数
目标是寻找一个低维映射 $f: \mathbf{x}_i \mapsto y_i \in \mathbb{R}$ （或推广到 $\mathbb{R}^p$ ）使得相邻点在低维空间中依然紧密。该目标函数自然地定义为
$\sum_{i,j} (y_i - y_j)^2 w_{ij}$
这个式子在数值上度量了低维表示中“断裂”的局部结构。
通过谱分解求解最优嵌入
对目标函数做适当约束后，可以得到一个广义特征值问题，其小特征值对应的特征向量即为低维坐标。

（2）拉普拉斯矩阵构建过程

2.1局部邻域图与邻接矩阵

邻域选择：对每个数据点 $\mathbf{x}_i \in \mathbb{R}^D$ ，利用 k 近邻或 ϵ 邻域的方法构造图 G；
权重设置：定义权重 $w_{ij}$ 来衡量数据点之间的相似性，常用的有高斯核形式 $w_{ij} = \exp\Bigl(-\frac{\|\mathbf{x}_i-\mathbf{x}_j\|^2}{t}\Bigr)$ , 或者采用二值权重：若 i 与 j 为邻居，则 $w_{ij}=1$ ，否则 $w_{ij}=0$ 。
邻接矩阵：在图论中，邻接矩阵 W 是一个表示图中节点间边的加权矩阵。其元素 $w_{ij}$ 表示节点 $v_i$ 和节点 $v_j$ 之间的相似度或连接强度。对于无向图， $w_{ij}=w_{ji}$

2.2度矩阵

定义： 度矩阵 D 是一个对角矩阵，其中每个对角元素 $d_i$ 表示节点 $v_i$ 的度，即与连接的所有边的权重之和。度矩阵是图的结构的一个重要量化指标，能够体现每个节点的“重要性”。
形式： $D = \begin{pmatrix} d_1 & 0 & \cdots & 0 \\ 0 & d_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_N \end{pmatrix}$ 其中， $d_i$ 表示节点 $v_i$ 的度。

2.3拉普拉斯算子

拉普拉斯算子是一个广泛应用于数学、物理和机器学习中的重要微分算子。在图论中，拉普拉斯算子主要用来描述图的“平滑度”或“变化率”，并用于优化问题，如图的分割和聚类。

拉普拉斯算子的定义：

定义： 在图中，拉普拉斯算子通常表示为： $\Delta f = \nabla \cdot (\nabla f)$ 其中，∇ 表示梯度运算符，∇· 是散度，表示图上函数值的变化率。
应用： 拉普拉斯算子用来描述节点之间的平滑性，或者说是如何通过其邻居的值来平衡当前节点的函数值。在图上，拉普拉斯算子通过节点之间的关系来度量这种“平滑”特性。

离散拉普拉斯算子：

形式： 在离散化的图中，拉普拉斯算子的离散形式为： $\Delta f_i = \sum_{j \in N_i} w_{ij} (f_i - f_j)$ 其中， $N_i$ 是节点 $v_i$ 的邻居集合， $w_{ij}$ 是节点 $v_i$ 与邻居 $v_j$ 之间的权重（通常是边的权重）， $f_i$ 和 $f_j$ 是节点的函数值。

2.4拉普拉斯矩阵

对于离散化的拉普拉斯算子 $\Delta f_i = \sum_{j \in N_i} w_{ij} (f_i - f_j)$ ，可整理为：

$\Delta f_i = d_i f_i - w_i \cdot f$

其中， $d_i$ 是节点的度， $w_i$ 表示邻接矩阵的第 i 行。

拉普拉斯算子的离散化可以用矩阵表示出来。对所有的节点进行类似的处理，最终可以得到一个矩阵形式：

$\Delta f = \left( D - W \right) f = L f$

其中：

D 是度矩阵（degree matrix），它是一个对角矩阵，其中每个元素 $d_i$ 代表节点 $v_i$ 的度，即该节点的连接权重之和：
$d_i = \sum_{j \in N_i} w_{ij}$
W 是邻接矩阵（adjacency matrix），其中 $w_{ij}$ 是节点 $v_i$ 和 $v_j$ 之间的权重。
L 是拉普拉斯矩阵，即： $L = D - W$ ，它表示了图的结构以及节点之间的连接关系。

（3）拉普拉斯矩阵的性质

3.1半正定性

拉普拉斯矩阵 L = D - W 是半正定的。这意味着对于任意的向量 f ，我们都有：

$f^T L f = \frac{1}{2} \sum_{i,j=1}^N w_{ij}(f_i - f_j)^2 \geq 0$

这个公式的含义是，拉普拉斯矩阵的特征值非负，最小特征值为零。证明过程如下：

对于任意的 f，我们可以将上述表达式展开并整理成类似于能量的形式，表明其值为非负值，因此 L 是半正定的。

3.2最小特征值为零

拉普拉斯矩阵 L 的最小特征值为零，且对应的特征向量是常数向量（所有元素为1）。这个性质的证明依赖于图中所有节点度的定义：

$d_i = \sum_{j=1}^N w_{ij}, \quad L = D - W$

通过计算，得到矩阵 L 作用于特征向量 $\nu$ （其中所有元素均为1）时，结果为零：

$L \nu = (D - W) \nu = 0$

这证明了 L 具有零特征值，且特征向量是常数向量。

3.3零特征值与图的连通性

拉普拉斯矩阵的特征值中的零对应图的连通分量的数量。证明过程如下：

如果图是连通的，零特征值出现一次，表示该特征向量是全1向量。
如果图是由多个连通分量组成，零特征值的出现次数等于图的连通分量数。每个连通分量对应一个零特征值，并且该特征值的特征向量是常数向量。

3.4零特征值对应的特征向量是常数向量

当 L 作用于一个特征向量 f 并且 f 是零特征值对应的特征向量时， $Lf = 0$ ，表示 f 是常数向量。具体来说，假设：

$L f = \sum_{i,j=1}^N w_{ij}(f_i - f_j)^2 = 0$

这意味着，对于所有的 i 和 j，都有 $f_i = f_j$ ，即 f 是常数向量。

例子：

（4）拉普拉斯矩阵的规范化形式

4.1规范化的拉普拉斯矩阵

对称拉普拉斯矩阵 (Symmetric Laplacian):

对称拉普拉斯矩阵的定义是：
$L_{\text{sym}} = D^{-1/2} L D^{-1/2}$
其中 L 是原始的拉普拉斯矩阵 $L = D - W$ ，D 是度矩阵，W 是邻接矩阵。通过这种规范化，能够消除节点度对图的影响，从而使得不同规模或稀疏度的图能够在同一个标准下进行比较。这样处理后的拉普拉斯矩阵的特征值可以更好地反映图的结构特征。
随机游走拉普拉斯矩阵 (Random Walk Laplacian):

随机游走拉普拉斯矩阵的定义是：
$L_{\text{rm}} = D^{-1} L = I - D^{-1} W$
这个形式的拉普拉斯矩阵适用于描述随机游走过程。通过这个矩阵，可以分析随机游走在图中的传播特性。例如，随机游走的矩阵 $L_{\text{rm}}$ 可以帮助在图中进行聚类分析。

4.2 性质

对于任意向量 f，对称拉普拉斯矩阵 $L_{\text{sym}}$ 的作用可以表示为：
$f^T L_{\text{sym}} f = \frac{1}{2} \sum_{i,j=1}^N w_{ij} \left( \frac{f_i}{\sqrt{d_i}} - \frac{f_j}{\sqrt{d_j}} \right)^2$
这个性质表示了对称拉普拉斯矩阵在图上进行平滑操作的效果。通过规范化，特征值和特征向量在每个节点的影响被均衡化，避免了度大的节点对整个图结构的支配作用。
特征值与特征向量的关系：如果 $(\lambda, \nu)$ 是 $L_{\text{rm}}$ 的特征值和特征向量，则 $(\lambda, D^{-1/2} \nu)$ 是 $L_{\text{sym}}$ 的特征值和特征向量。这表明，随机游走拉普拉斯矩阵的特征值和特征向量与对称拉普拉斯矩阵通过一定的规范化关系相互转换。

4.3 应用

a. 提升模型的适应能力

规范化的拉普拉斯矩阵能够减少节点度的影响，提升模型对不同规模或稀疏度图的适应能力。例如，在图神经网络（GNN）中，规范化的拉普拉斯矩阵使得图中不同节点的贡献被公平地考虑，从而提高了模型对不同类型图的泛化能力。

b. 与图卷积网络 (GCN) 相关

规范化的拉普拉斯矩阵适用于图卷积网络（GCN）等模型，确保信息能够在图的邻域之间有效传播。GCN 是一种基于拉普拉斯矩阵的图信号处理方法，通过对拉普拉斯矩阵的特征值和特征向量的操作，可以对图进行有效的聚类、分类等任务。

c. 随机游走拉普拉斯矩阵的应用

规范化的随机游走拉普拉斯矩阵模型能够模拟随机游走过程的转移概率，广泛应用于计算节点之间的关系、图的传播模型（如 PageRank 算法）以及节点之间的信息流传输。

《关于拉普拉斯矩阵更详细的理解在附录1》

（5）降维——降到一维的情况

5.1 降维的目标

在数据降维问题中，我们希望将高维数据点映射到低维空间，并尽可能保留其局部结构关系。对于一个不连通的图，每个连通分量可以独立进行降维处理。

设数据点的低维嵌入向量为：

$z = (z_1, z_2, ..., z_N)^T$

其中，每个 $z_i$ 是数据点 i 在一维降维空间中的表示。

目标函数

降维问题的优化目标是最小化以下目标函数：

$\frac{1}{2} \sum_{i,j=1}^{N} (z_i - z_j)^2 w_{ij}$

其中， $w_{ij}$ 是数据点 i 和 j 之间的权重。如果 $w_{ij}$ 很大，则表示数据点 i 和 j 在原空间中接近，因此在降维空间中它们的表示 $z_i$ 和 $z_j$ 也应尽量接近，即 $(z_i - z_j)^2$ 应该尽可能小。

这一优化目标确保了相似的点在降维空间中仍然相似。

5.2 目标函数转换

利用拉普拉斯矩阵 $L = D - W$ ，可以将目标函数重新表达为：

$\frac{1}{2} \sum_{i,j=1}^{N} (z_i - z_j)^2 w_{ij}$

展开后：

$= \frac{1}{2} \sum_{i,j=1}^{N} z_i^2 w_{ij} + \frac{1}{2} \sum_{i,j=1}^{N} z_j^2 w_{ij} - \sum_{i,j=1}^{N} z_i z_j w_{ij}$

根据度矩阵 D 的定义 $d_i = \sum_j w_{ij}$ ，上述表达式可以转换为：

$\sum_{i=1}^{N} z_i^2 d_i - \sum_{i,j=1}^{N} z_i z_j w_{ij}$

$= \sum_{i,j=1}^{N} z_i (d_i - w_{ij}) z_j = z^T (D - W) z = z^T L z$

因此，目标函数最终被转换为：

$\min z^T L z$

5.3 约束条件：尺度不变性

如果不加任何约束，目标函数的最优解可能是所有 $z_i$ 相同的平凡解。这种情况下，所有点都映射到相同位置，降维失去意义。因此，我们添加两个约束条件：

去除平移自由度 (均值为 0)：
$z^T D \mathbf{1} = 0$
这确保嵌入向量的均值为 0，从而消除平移不变性。
去除尺度因子 (单位化约束)：
$z^T D z = 1$
这确保嵌入向量不会因尺度因素而影响最终结果，使得降维后数据均匀分布。

5.4目标优化问题

最终的优化问题变为：

$\min_{z} z^T L z \quad \text{s.t.} \quad z^T D z = 1$

这个约束优化问题可以通过 拉格朗日乘子法 求解：

$L = z^T L z - \lambda (z^T D z - 1)$

对 z 求偏导并令其等于 0：

$Lz = \lambda D z$

这个方程是 广义特征值问题：

$D^{-1} L z = \lambda z$

$L_{rm} z = \lambda z$

其中 $L_{rm}$ 是 随机游走拉普拉斯矩阵，该方法的解为其最小的非零特征值对应的特征向量。

5.5 目标函数优化

由于：

$z^T L z = \lambda z^T D z = \lambda$

为了最小化目标函数，我们选择最小的 非零特征值 $\lambda$ 对应的特征向量作为降维后的表示。注意，最小的特征值 $\lambda = 0$ 的对应特征向量是全 1 向量（无信息），因此我们选择 第二小的特征值对应的特征向量 作为嵌入向量。

5.6 实例

一个简单的例子：

邻接矩阵 W：

$W = \begin{bmatrix} 0 & 0.8 & 0.8 & 0 & 0 \\ 0.8 & 0 & 0.8 & 0 & 0 \\ 0.8 & 0.8 & 0 & 0.1 & 0 \\ 0 & 0 & 0.1 & 0 & 0.9 \\ 0 & 0 & 0 & 0.9 & 0 \end{bmatrix}$

度矩阵 D： $D = \text{diag}(1.6, 1.6, 1.7, 1, 0.9)$
拉普拉斯矩阵 $L = D - W$ ：

$L = \begin{bmatrix} 1.6 & -0.8 & -0.8 & 0 & 0 \\ -0.8 & 1.6 & -0.8 & 0 & 0 \\ -0.8 & -0.8 & 1.7 & -0.1 & 0 \\ 0 & 0 & -0.1 & 1 & -0.9 \\ 0 & 0 & 0 & -0.9 & 0.9 \end{bmatrix}$

随机游走拉普拉斯矩阵 $L_{rm}$ ： $L_{rm} = I - D^{-1} W$ 其特征值为： $0 < 0.0693 < 1.4773 < 1.5 < 1.9534$ 选择第二小的特征值 0.0693 对应的特征向量： $v \approx \begin{bmatrix} -0.3923 \\ -0.3923 \\ -0.3379 \\ 0.9307 \\ 1 \end{bmatrix}$

这个特征向量给出了降维到一维的表示。

（6）降维——降维后非一维

拉普拉斯特征映射（Laplacian Eigenmaps, LE）是一种基于图拉普拉斯矩阵的非线性降维方法，主要用于保持数据的局部几何结构，同时将数据嵌入到低维空间中。之前的分析主要是针对 一维降维情况，而这里的分析涉及 降维到更高维 的情况，即降维到 D′ 维。

6.1高维拉普拉斯特征映射的目标

在一维降维中，我们使用 $z = (z_1, z_2, ..., z_N)^T$ 表示数据点的低维表示。而在更高维的情况下，我们使用一个 $N \times D'$ 维矩阵 Z 进行降维：

$Z = (z_1, z_2, ..., z_N)^T$

其中，每个 $z_i$ 是数据点 $x_i$ 在降维空间的 D′ 维表示。

目标函数

$\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} ||z_i - z_j||^2 w_{ij}$

该目标函数的含义：

通过加权二范数 $|z_i - z_j||^2$ 控制数据点的相对位置
$w_{ij}$ 作为相似性权重，保证相似数据点在低维空间中保持靠近

6.2 目标函数的转换

目标函数可以展开为：

$\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} (z_i^T z_i - 2z_i^T z_j + z_j^T z_j) w_{ij}$

使用 度矩阵 D 和 邻接矩阵 W 进行重构：

$\sum_{i=1}^{N} \sum_{j=1}^{N} w_{ij} z_i^T z_i = \sum_{i=1}^{N} d_i z_i^T z_i$

$\sum_{i=1}^{N} \sum_{j=1}^{N} w_{ij} z_i^T z_j = \text{tr}(Z^T W Z)$

最终目标函数可以写成：

$\text{tr}(Z^T L Z)$

其中， $L = D - W$ 是 拉普拉斯矩阵。

6.3 约束条件

为了防止退化解（例如所有数据点映射到同一点），引入 标准化约束：

均值约束：
$Z^T D \mathbf{1} = 0$
该约束确保降维后的数据均值为 0，防止整体平移。
方差归一化：
$Z^T D Z = I$
该约束用于消除尺度不变性，使得嵌入向量不会坍缩到零向量。

6.4 目标函数优化

带约束的优化问题可写成：

$\min_Z \text{tr}(Z^T L Z), \quad \text{s.t. } Z^T D Z = I, Z^T D \mathbf{1} = 0$

使用 拉格朗日乘子法，构造拉格朗日函数：

$L = \text{tr}(Z^T L Z) - \text{tr}(\Lambda(Z^T D Z - I))$

对 Z 求偏导，并令其等于 0：

$\frac{\partial L}{\partial Z} = 2LZ - 2D Z \Lambda = 0$

即：

$L Z = D Z \Lambda$

这实际上是一个 广义特征值问题：

$D^{-1} L Z = Z \Lambda$

这说明 Z 由 随机游走拉普拉斯矩阵 $D^{-1} L$ 的最小非零特征值对应的特征向量 组成。

6.5 选择特征向量进行降维

计算随机游走拉普拉斯矩阵的特征值和特征向量
选择 最小非零特征值对应的特征向量 作为降维空间的基
令： $Z = (v_2, v_3, ..., v_{D'+1})$ 其中， $v_k$ 为对应于第 k 小特征值的特征向量

结论： 目标函数 $\text{tr}(Z^T L Z)$ 取极小值时，对应最小特征值 $\lambda_i$ 之和。因此，降维后的空间由 最小非零特征值对应的特征向量 组成。

（7）拉普拉斯特征映射的应用

7.1 低维嵌入

通过选取 D′ 个最小非零特征值对应的特征向量 作为新的坐标，Laplacian Eigenmaps 能够将数据从高维空间降维到 D′ 维空间。

7.2 数据可视化

如 Swiss Roll 数据集：

高维数据通过 拉普拉斯特征映射 展开到 2D/3D 空间
低维表示保持数据的局部几何结构
可以用于聚类、数据降维、流形学习等任务

7.3 参数影响

ttt 控制权重矩阵 $W_{ij} = e^{-\frac{||x_i - x_j||^2}{t}}$
N 控制邻域大小，影响局部结构的保留程度
适当调整参数 t 和 N 可以获得更好的降维效果

（8）本质分析

8.1 理论本质

局部保持思想
Laplacian Eigenmaps 的基本出发点是：局部邻域内数据点间的关系反映了流形的局部结构。通过构造加权邻域图并利用图拉普拉斯矩阵 L，我们将这种局部相似性内嵌到目标函数中，从而确保在低维嵌入中相邻数据点依然保持接近。
谱图理论
该方法与谱图理论密切相关。实际上，图拉普拉斯矩阵 L 的谱结构（即其特征值和特征向量）携带了图的几何信息，尤其是关于图的平滑性与连通性。低频部分（小特征值对应的特征向量）通常反映了数据的全局结构，而在 Laplacian Eigenmaps 中，我们重点关注保留局部信息，因此舍弃全局常数解后，剩下的低频解正好给出了良好的嵌入。
与流形上的拉普拉斯-贝尔特拉米算子的联系
在连续情形下，数据流形的几何可以通过拉普拉斯-贝特拉米算子刻画，而图拉普拉斯矩阵可以看作对这种算子的离散近似。通过谱分解，我们实际上是在近似求解流形上的本征函数，这些本征函数可以用于构造流形上的坐标系。

8.2 优势与局限

优势
- 局部结构保持：通过最小化目标函数 $y^\top L\,y$ ，确保了局部邻域内的点在低维嵌入中紧密相连；
- 非线性降维：适用于具有非线性结构的数据，能够揭示流形的内在低维结构；
- 理论基础坚实：基于谱图理论和拉普拉斯-贝特拉米算子的离散近似，具有较强的数学支撑。
局限性
- 参数敏感性：邻域构造中 k 或 ϵ 的选取对结果有较大影响；
- 全局结构难以捕获：由于重点关注局部关系，方法可能无法充分揭示数据的全局几何结构；
- 计算代价：对于大规模数据，需要构造并分解较大的稀疏矩阵，计算量和内存需求可能较高。

2、t-NSE

（1）算法思想与基本流程

t-SNE 的目标是将高维数据映射到低维空间，同时尽量保留数据在高维空间中的局部邻域结构。其基本思路是：

高维相似性建模
对于每个数据点，利用高维空间中的距离计算相似性，并将其转化为条件概率，反映一个点选择其他点为邻居的概率。
低维相似性建模
在低维空间中，用一个分布（通常是重尾的 Student t 分布）来计算低维点之间的相似性概率，以缓解降维过程中出现的“拥挤问题”（crowding problem）。
最小化分布间差异
采用 Kullback-Leibler 散度（KL 散度）作为损失函数，使得高维相似性分布与低维相似性分布之间的差异最小，从而得到低维表示。

（2）高维相似性概率的构造

为什么要使用概率表示相似度而不是使用低维的距离呢？

由于在高维的空间中，最小距离的也很远，要想降到低维保持距离不变做不到，而且最小距离与最大距离差别的倍数不太明显，直接按距离降维时的区分度也不是很好。如下图：

设有 n 个数据点 $\{\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_n\}$ （ $\mathbf{x}_i \in \mathbb{R}^D$ ），对于任意数据点 $\mathbf{x}_i$ ：

2.1 计算条件概率

首先，利用高斯核将点 $\mathbf{x}_j$ 相对于 $\mathbf{x}_i$ 的相似性表示为条件概率：

$p_{j|i} = \frac{\exp\left(-\frac{\|\mathbf{x}_i-\mathbf{x}_j\|^2}{2\sigma_i^2}\right)}{\sum_{k\neq i} \exp\left(-\frac{\|\mathbf{x}_i-\mathbf{x}_k\|^2}{2\sigma_i^2}\right)}$

其中， $\sigma_i$ 为针对每个点自适应的尺度参数，通过设定一个固定的“perplexity”（困惑度）来确定，从而平衡局部邻域的大小。

2.2 构造对称相似性

由于 $\sigma_i$ 和 $\sigma_j$ 不一定相等，所以 $p_{j|i}$ 和 $p_{i|j}$ 不一定相等，因此相似性需要平均一下。

为确保对称性，定义：

$p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n},\quad i\neq j, \quad p_{ii}=0$

这样，所有 $p_{ij}$ 构成了高维数据点之间的相似性概率分布，总和为 1。分母是2n 保证了对所有 n 个数据点进行规范化，确保整个相似性矩阵的概率总和为 1。

2.3 有关尺度参数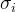 $\sigma_i$ 的详细分析

每个样本的尺度参数不一样，一样可以吗？如何通过困惑度来设定尺度参数的？

每个样本的尺度参数不一样的原因：
每个数据点的尺度参数（ $\sigma_i$ ）是与该点的局部密度有关的。局部密度较大的区域，点之间的距离较小，因此需要较小的尺度参数来确保这些点之间的相似度较高；而在稀疏的区域，数据点之间距离较远，需要更大的尺度参数才能确保这些点之间的相似度不会过低。
因此，每个点的尺度参数都不一样，是为了能自适应地调整相似性的计算，使得不同区域的局部结构能得到适当保留。
如果每个样本的尺度参数一样会有什么问题：
如果所有点使用相同的尺度参数，那么在高维空间中密集的区域会因为尺度参数太大而导致邻居过多，影响局部结构的细节；而稀疏区域则可能因为尺度参数过小而忽视较远点之间的潜在相似性。结果可能会导致降维后的表示失去一些重要的局部结构特征。
如何通过困惑度来设定尺度参数：
困惑度（Perplexity）是一种衡量概率分布宽度的指标，定义为：
$\text{perplexity}(p_{i|j}) = 2^{H(p_{i|j})}, \quad H(p_{i|j}) = -\sum_j p_{j|i} \log p_{j|i}$
这里的 $H(p_{i|j})$ 是高维空间中条件概率的熵。困惑度控制了邻域的大小，可以通过调节困惑度来自动调整每个点的尺度参数，使得每个数据点的邻域包含大约相同的信息量。通常通过交叉验证或启发式方法来选择一个合适的困惑度值。
困惑度 大致表示每个点有效的邻居数目。

2.4 困惑度对降维结果的影响

困惑度（Perplexity）影响 t-SNE 中相似性计算的范围，它与数据点的尺度参数 $\sigma_i$ 密切相关：

困惑度的作用：
困惑度控制了每个点在高维空间中考虑多少邻居。较小的困惑度会使得每个点只关注最近的邻居，从而关注局部结构；而较大的困惑度则会扩大每个点的邻域范围，从而捕捉更多的全局结构。
困惑度对降维结果的影响：
- 低困惑度：当困惑度较小时，算法会关注数据点的局部结构，导致降维结果中的簇更加紧密，但可能会失去全局的结构信息。
- 高困惑度：当困惑度较大时，算法将考虑更广泛的邻居，这可能会导致全局结构更好地反映出来，但可能牺牲一些细粒度的局部结构。
困惑度的选择应该与数据的特性（如数据的密度、局部结构等）相匹配，通常需要通过交叉验证来选择最优值。

（3）低维相似性概率的构造

3.1 低维构造过程

设低维嵌入为 $\{\mathbf{y}_1, \mathbf{y}_2, \dots, \mathbf{y}_n\}$ ，其中 $\mathbf{y}_i \in \mathbb{R}^d$ （通常 d=2 或 3）。为了避免高维到低维的拥挤问题，采用重尾分布（Student t 分布， $\nu=1$ 的情形即柯西分布）计算低维相似性：

$q_{ij} = \frac{\left(1+\|\mathbf{y}_i-\mathbf{y}_j\|^2\right)^{-1}}{\sum_{k\neq l}\left(1+\|\mathbf{y}_k-\mathbf{y}_l\|^2\right)^{-1}},\quad q_{ii}=0$

这种选择使得在低维空间中，远距离点仍有较小但非零的相似性，缓解了“拥挤”效应。

3.2 t 分布就可以缓解“拥挤”效应

“拥挤效应”：
在 t-SNE 中，由于数据降维的空间通常维度较低（例如 2D 或 3D），大量的高维数据点会被压缩到相对有限的低维空间中，导致低维嵌入中点之间的距离变得过于接近，从而造成所谓的“拥挤效应”。这会使得数据的局部结构不能得到很好的保留。
t 分布的作用：
t 分布，特别是自由度为 1 的 Student t 分布（即 Cauchy 分布），相对于高斯分布有更重的尾部。这意味着在低维空间中，t 分布对远距离数据点的相似性保持了非零值，从而避免了由于过度压缩而使远距离点之间的关系消失。与高斯分布相比，t 分布允许远离的点仍然具有某种程度的相似性，因此能够缓解“拥挤效应”。

换句话说，使用 t 分布能够帮助低维嵌入中的点更加均匀地分布，减小点之间的挤压效应，并且使得相似度较大的点仍然有较大的相似性概率。
高维时使用的是高斯分布来构造的概率，而低维时使用t分布来构造概率可以使得相似的点在低维空间中更近，而不相似的点更远。

（4）成本函数与优化目标

用KL散度(Kullback-Leibler Divergence)衡量两个分布之间的距离。

t-SNE 定义的成本函数为高维分布 P 与低维分布 Q 之间的 KL 散度：

$C = KL(P\|Q) = \sum_{i\neq j} p_{ij} \log\frac{p_{ij}}{q_{ij}}$

最小化该成本函数，即希望低维嵌入中的点对相似性 $q_{ij}$ 能够尽可能匹配高维中的相似性 $p_{ij}$ ，从而保留原始数据的局部结构。

KL散度作为目标函数带来的影响

KL散度不是凸函数，具有不同初始值的多次运行将收敛于KL散度函数的局部最小值中，会获得不同的结果。因此，可尝试不同的随机数种子，并选择具有最低KL散度值的结果。
KL 散度的非对称性：KL 散度本质上是衡量两个概率分布之间的不对称差异，定义为：

$D_{KL}(P \| Q) = \sum_i p_i \log \frac{p_i}{q_i}$

显然，P 和 Q 不一定对称，意味着 $D_{KL}(P \| Q)$ 不等于 $D_{KL}(Q \| P)$ ，因此可以实现非对称性。这是因为 KL 散度关注的是高维分布 P 与低维分布 Q 之间的差异，而高维数据中的邻居关系对低维嵌入中的影响会更大，因此高维相似性 $p_{ij}$ 对低维映射的影响较为突出。

KL 散度的非对称性使得模型更关注局部结构

非对称性的好处：
非对称性使得 KL 散度能够关注更重要的“高维相似性”。这种非对称性是 t-SNE 在优化过程中有意识地引入的，使得算法能够优先保持那些高维中更重要的局部结构，而对于那些低维中不重要的点对，优化的程度较小。
非对称性是好还是坏？
非对称性是 t-SNE 算法设计的一个特性，并不是一种缺陷。它有助于使得 t-SNE 能够更聚焦于高维数据中的局部结构，并且通过这种方式来实现降维中的信息保留。

（5）梯度推导与优化

为采用梯度下降法优化嵌入，需计算关于低维坐标 $\mathbf{y}_i$ 的梯度。对成本函数求导可得（这里给出推导结果）：

$\frac{\partial C}{\partial \mathbf{y}_i} = 4 \sum_{j} (p_{ij}-q_{ij}) \frac{\mathbf{y}_i-\mathbf{y}_j}{1+\|\mathbf{y}_i-\mathbf{y}_j\|^2}$

5.1 推导简述

利用 $q_{ij}$ 关于 $\mathbf{y}_i$ 的显式表达式，先计算对 $\mathbf{y}_i$ 的偏导数；
注意到分母中的归一化项也依赖于 $\mathbf{y}_i$ ，在求导时需要使用链式法则；
最终经过整理，可以得到上式，其中系数 4 是为了方便数值稳定性而引入的常数。

该梯度表达式直观地表示：

当 $p_{ij}>q_{ij}$ 时，即高维中相似但低维中距离偏远，梯度驱动 $\mathbf{y}_i$ 向 $\mathbf{y}_j$ 靠拢；
反之，当 $q_{ij}>p_{ij}$ 时，会推动它们分开。

（6）本质分析与几何意义

6.1 保持局部结构

局部保真：
t-SNE 主要关注局部邻域内的相似性匹配，通过最小化 KL 散度，使得在高维空间中相似的数据点在低维空间中依然相邻。低维相似性 qijq_{ij}qij 受距离 $\|\mathbf{y}_i-\mathbf{y}_j\|$ 的强烈影响，从而确保局部结构得以保留。

6.2 “拥挤问题”与重尾分布

拥挤问题：
在高维到低维映射中，许多数据点会被迫挤到低维空间的有限区域内。若直接使用高斯核构造低维概率，较远点之间的相似性会过快衰减，导致局部结构难以区分。
重尾分布的作用：
使用 t 分布（重尾分布）使得低维空间中较远数据点的相似性仍然有非零值，有助于防止不同簇之间完全坍缩，同时允许较为准确地反映局部相似性。

6.3 KL 散度的非对称性

非对称性与局部敏感：
KL 散度是非对称的，它更关注那些高维中相似度较高的点对（即 $p_{ij}$ 较大处）的匹配情况。这种设计使得算法更强调局部结构的精确保留，而对远距离点的不匹配则不那么敏感。

6.4 全局结构与局部结构的平衡

局部优先：
t-SNE 在优化过程中主要保证局部邻域内的关系，因而在全局结构上可能不如其他方法（如 PCA 或 Isomap）那样保留大尺度结构。
直观解释：
从几何上看，t-SNE 的低维嵌入能看作是一种“软分簇”方法，其中相似的数据点形成了紧密的簇，而不同簇之间的相对位置虽不一定精确反映高维中的距离关系，但能直观展示局部相似性。

6.5 t-SNE 中簇之间的距离并不表示相似度

局部与全局结构的不同：
t-SNE 主要专注于保留数据的局部结构，即相似点之间的关系。它优化的是点之间在高维空间的相似度映射到低维空间的相似度。由于 t-SNE 在降维过程中更多关注于保持局部结构，它并不关心或准确反映簇与簇之间的全局结构或相似度。
簇之间的距离：
在 t-SNE 中，簇与簇之间的相对距离并不一定反映其在高维空间中的相似性。因为低维空间中的簇间距离更多地受到局部嵌入结构的影响，尤其是通过 t 分布进行平滑处理后，远距离点之间的关系可能被压缩或调整，这可能导致簇与簇之间的距离并不准确地反映它们的高维相似度。

3、UMAP

UMAP与经典的降维算法（例如t-SNE）相似，但是UMAP在速度和结构保持上都有显著优势。

t-SNE与UMAP的对比： UMAP的速度比t-SNE更快，且可以处理更大的数据集。通过随机梯度下降，UMAP能够有效处理降维，同时在全局结构上保持更好的一致性。
UMAP的优势： UMAP不仅用于数据可视化，还可以有效地生成低维表示，使得原始数据的结构得以保留。

（1）算法总体思路

UMAP 是一种非线性降维方法，其基本思想是：

构造高维数据的模糊流形结构：利用数据在原始空间中的距离信息构造一个局部的模糊单纯形集（fuzzy simplicial set），反映各点之间的局部连接关系。
构造低维嵌入的相似性结构：在低维空间中设计一个类似的概率分布（通常具有重尾性质），以便能够对抗降维过程中可能出现的拥挤问题。
优化全局一致性：通过最小化高维与低维之间的结构差异（通常采用交叉熵形式的目标函数），使得低维嵌入能较好地保留高维局部结构。

UMAP 同时借鉴了流形学习和代数拓扑中的思想，将数据近似看作嵌入在流形上《详细解释见附录3》，然后利用“模糊集合”描述局部连接结构，进而构造全局的拓扑表示。

（2）高维模糊流形构造

2.1 局部距离及局部连通性

对于数据点 $x_i \in \mathbb{R}^D$ （共 n 个），UMAP 首先采用某种距离度量（例如欧氏距离）计算点与点之间的距离 $d(x_i, x_j)$ 。为了捕捉局部结构，UMAP 为每个点自适应地确定两个重要参数：

局部连接偏移 $\rho_i$ ：
定义为点 $x_i$ 到其最近邻（不为自身）的距离。它保证在局部范围内至少有一个连接是无“距离惩罚”的，即
$\rho_i = \min_{j\neq i} \, d(x_i,x_j)$
这样，如果某个点处于一个非常稠密的区域，它与最近邻的距离较小；若在稀疏区域，则 $\rho_i$ 较大。
局部尺度参数 $\sigma_i$ ：
通过调整 $\sigma_i$ ，使得点 $x_i$ 的局部邻域中，邻居的加权相似度达到一个预设的“局部信息量”。通常要求：
$\sum_{j} \exp\left(-\frac{\max(0,d(x_i,x_j)-\rho_i)}{\sigma_i}\right) = \log_2(k)$
其中 k 是用户指定的邻居数（类似 t-SNE 中的困惑度概念）。这种方式保证每个点都有大致相同的信息量，从而适应不同密度的数据区域。对每个点，通常采用二分搜索来求解合适的 $\sigma_i$ 。

2.2 定义高维局部相似性

利用上述参数，定义点 $x_i$ 对 $x_j$ 的条件隶属度（或者说相似性）：

$\mu_{i|j} = \exp\left(-\frac{\max(0,d(x_i,x_j)-\rho_i)}{\sigma_i}\right)$

这个公式保证：

当 $d(x_i,x_j)$ 小于或等于 $\rho_i$ 时， $\mu_{i|j}=1$ （即认为 $x_j$ 与 $x_i$ 在局部内完全连接）；
当距离超出 $\rho_i$ 后，依靠指数衰减给出一个递减的相似性度量。

为了得到对称的相似性，UMAP 使用**模糊联合（fuzzy union）**的方式：

$\mu_{ij} = \mu_{i|j} + \mu_{j|i} - \mu_{i|j}\cdot \mu_{j|i}$

该公式的设计保证了结果处于 $[0,1]$ 区间，并且能捕捉到两边观点的结合，构成整个数据集的高维模糊单纯形集。《详细解释见附录4》

（3）低维嵌入的相似性构造

在低维空间中（通常 $y_i \in \mathbb{R}^d$ ，d=2 或 3），UMAP 同样构造一套相似性概率分布。为了应对降维时的拥挤问题，UMAP 采用一个具有重尾性质的函数形式：

$\tilde{\mu}_{ij} = \frac{1}{1 + a\,\|y_i - y_j\|^{2b}}$

其中参数 a 与 b 可通过拟合确定，使得当 $\|y_i-y_j\|$ 较小时，函数值接近 1，而当距离增大时，函数下降较慢，从而允许远处点依然保持非零的相似性。这样可以更好地分散低维嵌入，缓解局部拥挤现象。

《a和b的确定方式见附录2》

（4）目标函数与优化

UMAP 的目标是使低维空间中构造的模糊单纯形集尽可能接近高维数据所描述的模糊单纯形集。为此，采用了交叉熵（cross-entropy）作为损失函数，其形式为：

$C = \sum_{(i,j)} \left[\mu_{ij}\log\frac{\mu_{ij}}{\tilde{\mu}_{ij}} + (1-\mu_{ij})\log\frac{1-\mu_{ij}}{1-\tilde{\mu}_{ij}}\right]$

这个目标函数可以理解为：

对于那些高维中相似度高（ $\mu_{ij}$ 接近 1）的点对，希望低维中 $\tilde{\mu}_{ij}$ 也接近 1；
对于相似度低的点对，则希望低维中也不出现错误的高相似度。

由于交叉熵天然具有不对称性（类似 KL 散度），这种设计使得优化过程中对局部连接（即 $\mu_{ij}$ 较大处）的不匹配给予更多惩罚，而对全局远距离的点对（ $\mu_{ij}$ 较小）惩罚较少，从而更加关注局部结构的保留。

优化方法

为求解低维嵌入，UMAP 通常采用随机梯度下降（SGD）或其变种，并辅以负采样技术（negative sampling），使得只对重要的点对进行更新，从而大幅提高计算效率。梯度可以从上述交叉熵损失中求得，并针对 $y_i$ 进行更新。

（5）算法本质与几何意义

5.1 模糊单纯形集的拓扑描述

UMAP 的核心在于用模糊单纯形集描述数据的局部拓扑结构，这种描述方法源自代数拓扑学。它通过为每个局部邻域赋予隶属度，构造出一个能够捕捉高维局部结构的拓扑模型。然后，低维嵌入过程就是寻找一个低维模糊集合，使得两者之间的拓扑结构尽可能一致。

5.2 局部结构与全局结构

局部结构保留：
通过自适应尺度参数 $\rho_i$ 和 $\sigma_i$ ，每个点在高维空间中的局部邻域被精细描述，确保在局部区域内相似性关系被准确捕捉。优化过程主要集中于匹配这些局部隶属度，从而使得低维嵌入在保持局部连通性上表现优秀。
全局结构的影响：
尽管 UMAP 优先保留局部结构，但通过构造全局的模糊单纯形集以及在优化中考虑所有点对（结合了正样本和负样本），一定程度上也能反映全局几何信息。不过，相比局部信息，全局距离在低维嵌入中可能会出现一定的扭曲，这也是许多非线性降维方法的共同特性。

5.3 重尾核的作用

低维嵌入采用的核函数 $\tilde{\mu}_{ij} = \frac{1}{1+a\|y_i-y_j\|^{2b}}$ 具有重尾特性，这意味着即使较远的点对也有非零的相似性。这样设计有助于：

缓解拥挤效应：防止低维空间中所有点都聚集在一起；
平衡局部与全局：在保持局部高相似性同时，允许远处点在一定程度上反映出彼此的存在。

（6）总结

UMAP 的核心流程可归纳为以下几点：

局部构造：对每个数据点，通过距离度量、自适应尺度参数和局部偏移 $\rho_i$ 构造条件隶属度，得到局部模糊单纯形表示。
全局对称化：利用模糊联合操作，将局部信息整合成一个对称的高维相似性矩阵（模糊单纯形集）。
低维相似性设计：在低维空间中，选用具有重尾性质的核函数来构造相似性分布。
优化目标：通过交叉熵形式的目标函数（类似于 KL 散度），在低维嵌入中重现高维数据的模糊拓扑结构，并采用 SGD 进行优化。

从数学与几何角度看，UMAP 是在保留局部邻域内的拓扑关系基础上，通过构造模糊集合和最小化交叉熵损失来寻找低维嵌入，使得局部结构得以良好保留，同时兼顾一定的全局信息。其高效性和良好的可视化效果使其成为近年来非常流行的降维方法之一。

附录

1、拉普拉斯矩阵

拉普拉斯矩阵（Laplacian Matrix）在 图论、信号处理、机器学习、降维方法 等多个领域中都有广泛应用。它是图结构的核心特征之一，提供了图的拓扑信息，可以用来描述 图的平滑度、连通性、谱聚类、降维等问题。

（1）拉普拉斯矩阵的定义

对于一个 无向加权图 $G = (V, E)$ ，其中：

$V = \{ v_1, v_2, ..., v_N \}$ 是图的 节点集合
E 是图的 边集合
W 是 邻接矩阵，即 $W_{ij}$ 表示节点 i 和 j 之间的边权重
D 是 度矩阵，对角元素 $D_{ii} = \sum_j W_{ij}$ ，表示节点 i 的度（连接权重之和）

拉普拉斯矩阵 L 定义为：

$L = D - W$

其中：

度矩阵 D 控制节点的局部信息
邻接矩阵 W 表示节点的连接关系

随机游走拉普拉斯矩阵：

$L_{rw} = I - D^{-1} W$

归一化拉普拉斯矩阵：

$L_{sym} = D^{-1/2} L D^{-1/2} = I - D^{-1/2} W D^{-1/2}$

这些不同变体在不同应用场景中具有不同的特性，主要用于 信号平滑、光谱聚类、流形学习、降维等任务。

（2）几何意义与直观理解

2.1 拉普拉斯矩阵的本质

拉普拉斯矩阵的核心思想是度量图中每个节点的局部变化，即：

如果一个图中的节点 紧密相连，它们的拉普拉斯值会很小。
如果某些节点的连接较为稀疏或孤立，它们的拉普拉斯值会较大。

用数学的方式理解：

为了说明拉普拉斯矩阵在保持局部结构方面的作用，我们考虑任一实向量 $x = (x_1,x_2,\dots,x_n)^\top$ 定义在图节点上，其二次型可以写为：

$\begin{aligned} x^\top L x &= x^\top (D - W)x = \sum_{i} D_{ii} x_i^2 - \sum_{i,j} W_{ij} x_i x_j \\ &= \sum_{i} \left(\sum_{j} W_{ij}\right)x_i^2 - \sum_{i,j} W_{ij} x_i x_j \\ &= \frac{1}{2} \sum_{i,j} W_{ij}\Bigl[(x_i^2 + x_j^2) - 2x_i x_j\Bigr] \\ &= \frac{1}{2} \sum_{i,j} W_{ij}(x_i - x_j)^2. \end{aligned}$

该表达式说明：

若相连的节点 i 与 j 在函数 x 上取值相近，则 $(x_i - x_j)^2$ 小，对应边的“平滑性”较好；
整个二次型 $x^\top L x$ 则衡量了函数 x 在图上整体的变化程度或“能量”。
在 Laplacian Eigenmaps 中，我们通过最小化此二次型（在合适的归一化约束下），可以得到低维表示，使得原本相似（权重较大）的数据点在低维空间中距离也较近。

表示数据 x 在图上的局部平滑度。如果 x 的值在连接的节点之间变化很小，那么这意味着 x 是 平滑的，也就是说 邻接的点应该具有相似的值。

2.2 直观理解

图的扩散（Graph Diffusion）

可以将拉普拉斯矩阵看作一个高斯分布的拉普拉斯算子，用于衡量数据点之间的平滑度。例如：

如果我们用拉普拉斯矩阵来模拟 热传导，那么 $e^{-tL}$ 可以看作是热扩散的模拟。
如果数据点在降维后保持局部平滑性，那么它们在降维空间中仍然是紧密相连的。

图的连通性

如果 G 是连通图，则 L 只有一个零特征值，其特征向量是常向量（所有分量相同）。
零特征值的个数表示连通分量的个数，这在聚类任务（如光谱聚类）中尤为重要。

拉普拉斯矩阵与欧几里得空间的关系

在欧几里得空间，拉普拉斯矩阵对应的是 拉普拉斯算子，用于计算曲面的光滑程度。
在图上，拉普拉斯矩阵描述的是数据点的局部结构和全局平滑性。

平滑性度量
拉普拉斯矩阵的二次型直观上度量了相邻节点之间值的差异。若两个数据点之间连接权重 $W_{ij}$ 较大（说明它们在高维空间中相似），那么在低维嵌入中我们希望 $x_i$ 与 $x_j$ 尽可能接近，从而使 $(x_i - x_j)^2$ 较小。通过最小化 $x^\top L x$ ，即鼓励整个映射函数在图上保持平滑。

数据内在结构的保留
Laplacian Eigenmaps 利用低频（对应较小特征值）的特征向量作为嵌入坐标，这些低频分量在图上变化缓慢，反映了数据的全局连通性和局部几何结构。相似数据点在低维空间中依然保持紧密，确保内在结构得以保留。

2.3几何意义

离散与连续的联系

离散拉普拉斯算子
在连续情形下，拉普拉斯算子 Δ 用来描述标量函数在一个区域内相对于其邻域的平均偏差，常用于描述扩散、热传导等现象。图拉普拉斯矩阵 L 是这一连续算子的离散化表示，通过邻域图来近似流形上的局部几何。
流形学习中的应用
当高维数据点服从某个低维流形时，拉普拉斯矩阵的谱分解可以看作是对流形上拉普拉斯-贝特拉米算子的近似求解。低频本征函数（特征向量）构成了流形上的自然坐标系，这些坐标能够揭示数据的内在低维结构。

谱分解与嵌入

低频特征的作用
在谱分解中，零特征值对应的常数函数被舍弃后，次小的几个特征值及其对应的特征向量能捕捉数据的全局连通性和局部几何结构。通过将数据点在这些特征向量上的坐标作为低维表示，Laplacian Eigenmaps 实现了数据的非线性降维。
几何直观
可以将拉普拉斯矩阵视为一个测量局部“曲率”或“变化率”的工具。如果一个数据点的值与其邻域中其他数据点的值相差较大，则说明在该点处数据分布发生了剧烈变化；而在低维嵌入中，力求使这些局部差异最小，从而反映出数据在高维空间中真实的局部结构和相似性。

（3）典型应用

拉普拉斯矩阵不仅用于降维，还在图神经网络（GNN）、谱聚类、半监督学习等领域中具有广泛应用。

3.1 谱聚类 (Spectral Clustering)

计算 L 的前 k 个最小非零特征值对应的特征向量
使用这些特征向量作为新空间的特征
进行 K-Means 聚类

3.2 图卷积网络 (GCN)

GCN 通过归一化拉普拉斯矩阵 $L_{sym}$ 进行特征传播： $H^{(l+1)} = \sigma(D^{-1/2} W D^{-1/2} H^{(l)} W)$
该方法通过拉普拉斯矩阵在图上进行平滑，使得相邻节点的表示更加相似

3.3 拉普拉斯特征映射（Laplacian Eigenmaps）

通过计算 L 的特征向量，寻找嵌入空间
适用于 非线性流形降维，如 Swiss Roll 展平

3.4半监督学习

在少量已标注数据的情况下，使用拉普拉斯正则化来平滑预测值
通过最小化 $f^T L f$ 来优化

2、在低维嵌入的相似性构造中，a和b的确定方式

在 UMAP 的低维相似性构造中，采用的核函数形式为

$\tilde{\mu}_{ij} = \frac{1}{1 + a\,\|y_i - y_j\|^{2b}}$

其中参数 a 和 b 控制着函数曲线的形状。下面详细说明这两个参数的确定方法和背后的原理。

（1）参数确定的基本思想

UMAP 希望低维空间中构造出的相似性（或连接强度）能够既在近距离内接近 1（表示非常相似），又在远距离时衰减到接近 0，从而达到缓解“拥挤效应”的目的。为了达到这个效果，UMAP 采用了一个具有重尾性质的函数 $\frac{1}{1+a\,x^{2b}}$ （其中 $x = \|y_i-y_j\|$ ），并希望该函数在某个特定距离（通常作为尺度参考，如 1.0）处取得预设的相似度值（例如 0.5），同时整体曲线与预期的衰减形状吻合。

（2）非线性曲线拟合过程

具体来说，确定 a 和 b 通常涉及以下步骤：

设定目标形状
定义一个目标衰减函数或给定目标条件。例如，可以要求：
- 当 x=0 时，函数值为 1；
- 当 x=1 时，函数值为某个指定值（如 0.5），这相当于定义了一个“边界”距离；
- 对于更大 x 的值，函数衰减的速度和形状符合数据中点之间理想的相似性衰减要求。
采样距离值
在一个适当的区间内（例如从 0 到若干个单位距离），采样一系列距离值 $x_i$ ，这些点将作为拟合的依据。
构造误差函数
采用非线性最小二乘的方式，构造误差函数，其形式类似于：
$\min_{a,b} \sum_{i} \left( \frac{1}{1 + a\,x_i^{2b}} - g(x_i) \right)^2$
其中 $g(x)$ 是预先设定的目标函数，反映了理想情况下距离与相似性之间的关系。
求解优化问题
利用非线性最小二乘法（例如 Levenberg-Marquardt 算法），找到使上述误差最小的 a 和 b。

（3）理解参数 a 和 b 的几何意义

参数 a：
主要控制了距离衰减曲线在整体上的“水平拉伸”或“压缩”。较大的 a 会使得相似性迅速衰减，较小的 a 则会使得相似性保持较高值较长距离。
参数 b：
控制衰减曲线的“形状”或“陡峭程度”。指数 2b 指定了距离的幂次，决定了远距离处相似性值下降的速率。通过调节 b 可以获得更加柔和或更为尖锐的衰减曲线。

在 UMAP 中，这两个参数是全局的，即在所有点对上都使用相同的 a 和 b，这有助于在低维空间中构造一个统一的相似性度量，并且能够较好地对抗低维嵌入中常见的拥挤问题。

（4）实际应用中的默认值

在 UMAP 的实际实现中，经过上述非线性曲线拟合过程后，通常会得到一组默认参数值。例如，在原始论文和开源实现中，常见的默认值大约为：

a≈1.929
b≈0.791

这组参数在很多实际数据集上都能产生较好的低维嵌入效果。当然，根据数据的具体分布和应用场景，也可以调整这些参数或重新拟合以获得更为理想的结果。

3、UMAP 如何借鉴流形学习和代数拓扑的思想，将数据近似看作嵌入在流形上

（1）流形学习的假设

低维流形假设
流形学习的基本假设是：虽然数据可能以高维形式存在，但它们实际上分布在一个嵌入在高维空间中的低维流形上。这意味着数据的“本质”结构远比它们的维度高得多时要低。
局部欧氏性质
在一个小邻域内，高维数据的欧氏距离可以很好地反映数据点之间的真实几何关系。UMAP 利用这一点，将局部距离关系转化为隶属度（或相似性）。

（2）代数拓扑与模糊单纯形集

单纯形与拓扑结构
代数拓扑中，单纯形（simplices）用于构造描述空间拓扑的复杂结构。例如，点、边、三角形、四面体等等都可以看作单纯形的不同维度。
模糊单纯形集
UMAP 引入了模糊集合的概念，每个数据点之间的关系不是简单的 0/1（连接或不连接），而是赋予一个连续的隶属度。这种模糊隶属度构造了一个模糊单纯形集，能捕捉局部连接的强弱关系，从而较好地保留数据的局部拓扑结构。

（3）数据嵌入与流形结构

高维到低维的映射
UMAP 的目标是找到一个低维嵌入，使得低维空间中数据点之间的连接关系（用模糊隶属度表示）尽可能与高维数据中构造出的模糊单纯形集相似。
保留局部拓扑
这种做法实际上就是在假设数据在高维空间中分布在某个低维流形上，然后利用局部邻域内的几何和拓扑信息，构造一个低维映射，使得原始流形的局部结构得以保留。

4、UMAP 如何通过模糊联合到对称的相似性

（1）有向邻域与局部隶属度

条件隶属度
对于每个数据点 $x_i$ ，UMAP 根据其局部距离信息定义了一个条件隶属度： $\mu_{i|j} = \exp\Big(-\frac{\max(0,\,d(x_i, x_j) - \rho_i)}{\sigma_i}\Big)$ ，这里 $\rho_i$ 是数据点 $x_i$ 到其最近邻的距离（用来消除局部噪声影响），而 $\sigma_i$ 是自适应尺度参数。这一项描述了从 $x_i$ 出发，数据点 $x_j$ 作为邻居的“隶属程度”，但这个量本质上是有方向的——即它描述了 $x_j$ 对 $x_i$ 的相似性，而反过来不一定相同。

（2）模糊联合构造对称性

对称化需求
为了构造一个全局对称的相似性矩阵，我们需要合并 $\mu_{i|j}$ 和 $\mu_{j|i}$ 。
模糊联合公式
UMAP 使用模糊集合理论中的“联合”运算，将两个方向的隶属度组合为一个对称的度量：，这一公式保证了：
- 如果任一方向上隶属度较高，则整体的 $\mu_{ij}$ 也会较高；
- 如果两个方向都低，则 $\mu_{ij}$ 保持较低；
- 且结果自然被限制在 $[0,1]$ 的区间内，符合概率或相似性度量的要求。

（3）几何和拓扑意义

整合局部信息
这种对称化方式将来自不同数据点局部邻域的信息整合起来，从而构造出一个整体的模糊单纯形集，能够更全面地描述数据的局部拓扑结构。
兼顾密度差异
不同数据点可能处于密度不同的区域，通过单独设定 $\sigma_i$ 和 $\rho_i$ 后，再利用模糊联合合并双向信息，可以较好地平衡不同区域内的相似性计算，避免因局部密度差异而导致的不对称问题。