强化学习的数学原理（1-3）

本课程笔记参考（西湖大学智能无人系统实验室-赵世钰）https://www.bilibili.com/video/BV1sd4y167NS/?spm_id_from=333.337.search-card.all.click

文献引用：S. Zhao, “Mathematical Foundations of Reinforcement Learning”, Tsinghua University Press and Springer Nature Press, 2024

课程介绍

一些推荐书籍（不一定适合初学者）

课程安排：

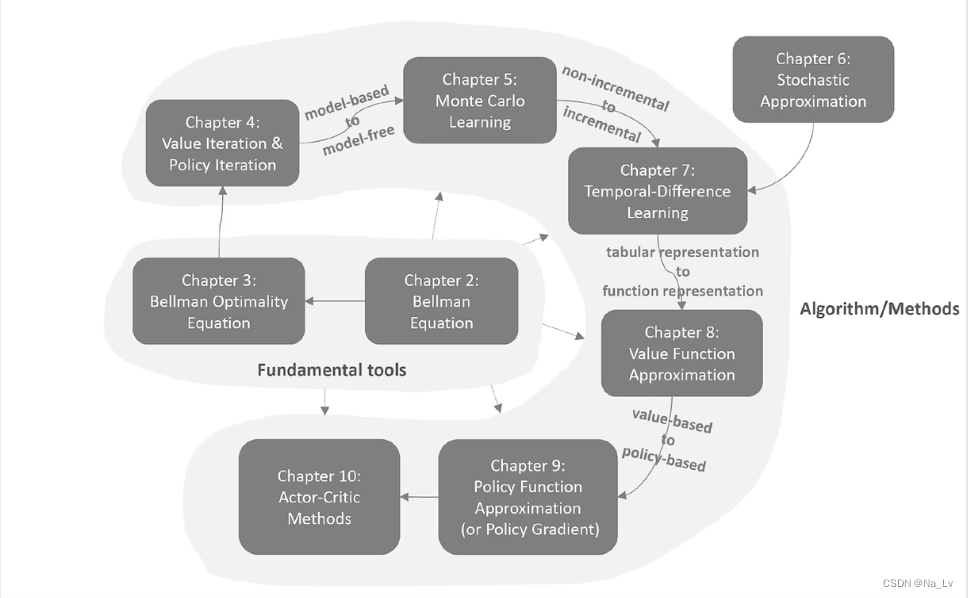
第一课 基本概念

概念	英文表示	字母表示
状态	State	$s_i$
状态空间	State Space	S = { s i } \mathcal{S}=\{s_i\} S={si​}
行动	Action	$a_i$
行动空间	Action Space	A ( s i ) = { a i } \mathcal{A}(s_i)=\{a_i\} A(si​)={ai​}
状态转移	State Transition	$s_1\stackrel{a_1}{\to }{s}_2$
状态转移概率	State Transition Probability	$p(s_2|s_1,a_1)$
策略	Policy	$\pi (a_1|s_1)$

需要注意的是
1、行动空间与状态有关
2、某一状态下采取各个行动的策略概率和为1
3、某一状态和某一行动下，转移后的状态概率和为1

  上述定义都是为了描述过程，那么如何体现人与机器的交互呢，引入下列定义：
1、Reword：当采取积极的行动，就给予正向奖励；采取消极的行动，就给予负面惩罚。
（reword以来当前状态和行动，而非下一状态）
2、Trajectory：一个 state-action-reward 链
3、Return：某trajectory得到的所有reword之和
4、Discount Rate : $\gamma \in [0,1)$ （为了解决return无限发散的问题）
5、Discounted Return：考虑Discount Rate后的Return，$\gamma$ 趋于0则更近视，趋于1则更远视
6、Episode（trial）：有Terminal State的Trajectory 【与之相反的是continue tasks】

  以上定义基本涵盖了所有后续可能会用到的知识，现在将其应用于一个马尔可夫过程框架中（markov decision process,MDP）
集合：$S$ 、$A(s)$ 、$R(s,a)$
概率分布：$p(s^{\prime }|s,a)$和$p(r|s,a)$
策略： $\pi (a|s)$ (在每个状态下动作的概率分布)
马尔可夫性：无记忆性

第二课 贝尔曼公式

首先还是回顾基础定义：

将上述定义应用在多步trajectory中，可以得到：

  于是state value 就是$G_t$的期望值:
$v_{\pi }(s)=\mathbb{E}[G_t|S_t=s]$
state value是关于状态$s$和策略$\pi$的函数
$▶$一个确定的trajectory求得的是return，从某一状态出发可能出现的多个trajectory的return的平均值是state value
下面推导Bellman 公式：




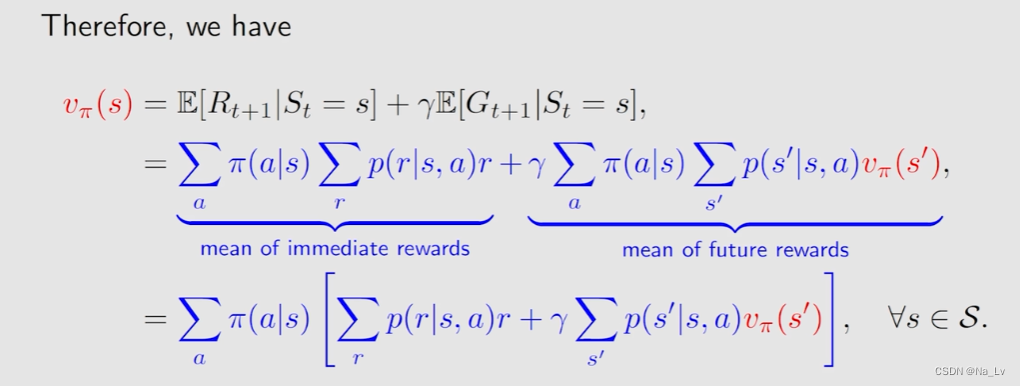
  观察上式可以得到相邻状态的state value间的关系，求解思想：BOOTSTRAPPING!
  同时为了求解需要已知$\pi (a|s)$、$p(r|s,a)$和$p(s^{\prime }|s,a)$。
$▶$一旦求解出$v_{\pi }(s)$，也就相当于评估了策略$\pi$，即policy evaluation。
$▶$$p(r|s,a)$和$p(s^{\prime }|s,a)$表示了动态模型。根据是否已知动态模型，可将问题分为两大类：model-based和model-free，分别会有对应的不同求解算法。
Bellman的矩阵形式


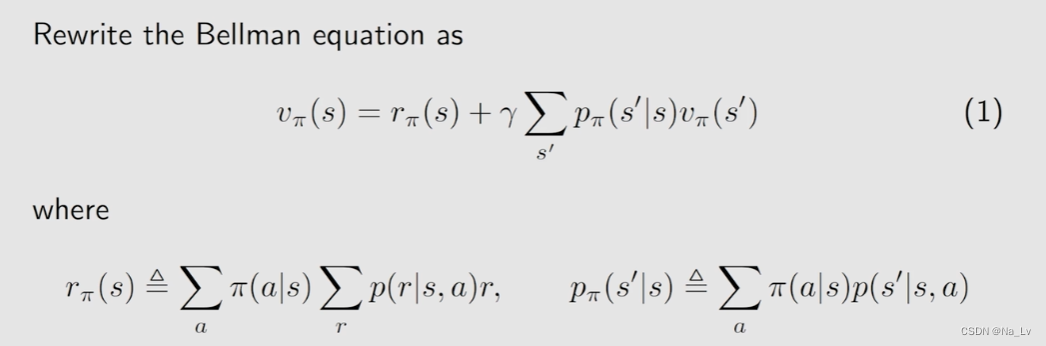
求解Bellman方程
  给定一个策略就可以写出其对应的Bellman公式，有Bellman公式就可以求解出State Value，求出State Value就可以用于评价该策略的优劣，所以本质是一个policy evaluation的过程。
  不同的策略可以得到相同的state value
方法1：closed form solution
$$v_{\pi }=(I-\gamma P_{\pi }{)}^{-1}{r}_{\pi }$$
方法2：iterative solution
$$v_{k+1}=r_{\pi }+\gamma P_{\pi }{v}_k$$
方法2的收敛性证明：

进而引入action value
$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$
依赖于状态、动作和策略（同一状态同一动作也会产生不同的下一状态，所以需要求期望）
$▶$action value 与 state value 的关系：

第三课 贝尔曼最优公式

贝尔曼最优公式的形式：

矩阵形式：

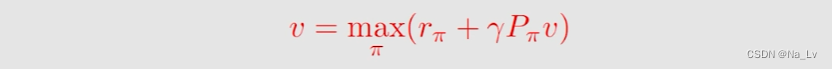
  针对上式一般假设模型已知（$p$,$r$,$\gamma$），$v(s)$和$\pi (s)$未知。即有两个未知数，求解时需先假定一个确定（一般是确定$v(s^{\prime })$，求解$\pi$，即求解每个action对应的$\pi (a|s)$）

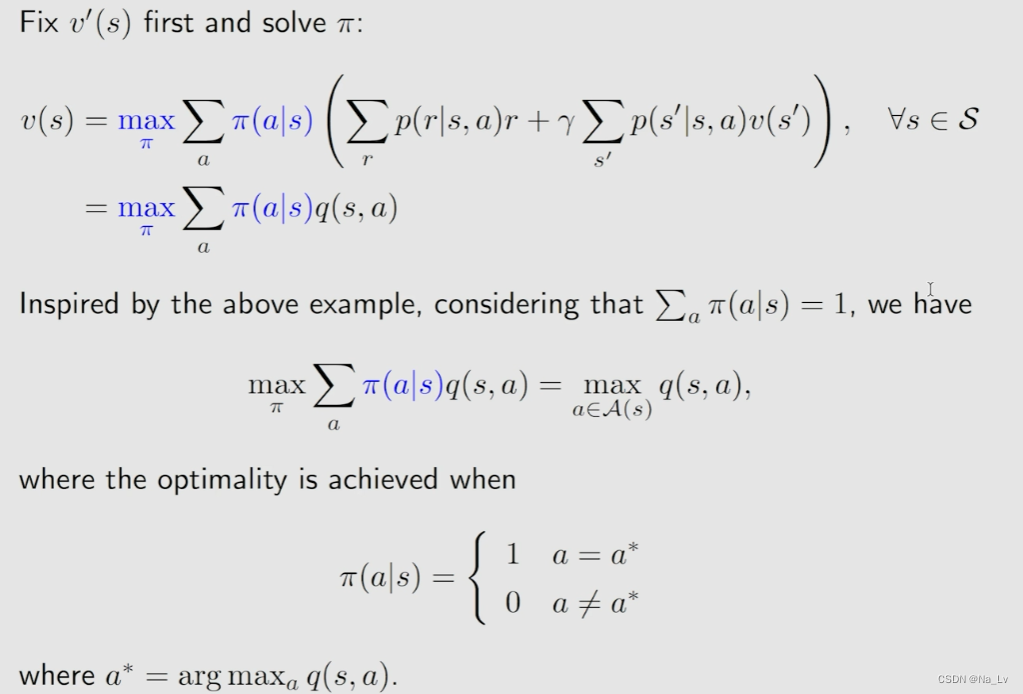
  BOE（bellman optimality equation）的求解借助了压缩映射不动点定理：

因此可以使用迭代算法求解：

详细的迭代算法写作：

最优性和唯一性：



一个推论（说明影响策略的是action value的相对大小，不是绝对大小）：