深入解析：利用PCA进行高效的点云配准

已于 2023-11-13 20:53:40 修改
阅读量2.2k 收藏 13
点赞数 3
文章标签： 人工智能 机器学习 深度学习
于 2023-11-13 20:39:53 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_61703832/article/details/134381287
版权

不知道这个框怎么删掉？？？

前言

在计算机视觉和三维建模领域，点云配准是一个基础且关键的任务。它涉及将来自不同视角或不同时间点的点云数据对齐到一个统一的坐标系统中。本文将深入探讨如何利用主成分分析（PCA）来实现高效且准确的点云配准。

一、主成分分析（PCA）概述

点云配准是三维重建、机器人导航、文化遗产保护等领域的关键技术。它的目标是找到两个或多个点云之间的最优对齐方式，以便于分析和处理。。

二、PCA点云配准的原理

PCA通过线性变换将原始数据转换到一个新的坐标系统中，使得在这个新坐标系统的第一坐标轴上的数据方差最大，第二坐标轴上的数据方差次之，依此类推。

在点云数据中，PCA可以识别出数据的主要方向（即主成分），这些方向通常对应于点云的几何特征，如长度、宽度和深度。

三、适用于PCA点云配准的点云特点

结构化点云：

  • PCA配准更适合于具有明显几何结构和特征的点云，如建筑物、机械零件等。
  • 在这些应用中，点云的主要方向和平面可以清晰地通过PCA识别出来。

规模适中的点云：

  • 对于规模适中的点云，PCA可以有效地处理和提取关键特征。对于极大规模的点云，可能需要先进行降采样或分割。

噪声水平适中的点云：

  • 虽然PCA具有一定的抗噪声能力，但过高的噪声水平仍然会影响其性能。因此，适度的预处理（如滤波）对于提高PCA配准的准确性是有帮助的。

最后，尤其注意点云密度对主成分方向的影响，吃过大亏。

代码：

// https://blog.csdn.net/fei_12138/article/details/118677416
// 运行成功了
#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/console/time.h>   
#include <boost/thread/thread.hpp>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/filters/voxel_grid.h>
#include <vtkAutoInit.h>
#include <Eigen/Core>
#include <Eigen/Eigenvalues>
#include<pcl/registration/correspondence_estimation.h>
#include <pcl/common/impl/transforms.hpp>

//计算向量u与向量v之间的夹角
void calRotation(Eigen::Vector3f u, Eigen::Vector3f v, double& angle, Eigen::Vector3f& vec);
//获取罗德里格斯旋转矩阵
Eigen::Matrix4f RodriguesMatrixTranslation(Eigen::Vector3f n, double angle);

int main()
{
	pcl::PointCloud<pcl::PointXYZ>::Ptr target(new pcl::PointCloud<pcl::PointXYZ>());//目标点云
	pcl::PointCloud<pcl::PointXYZ>::Ptr source(new pcl::PointCloud<pcl::PointXYZ>());//源点云
	//pcl::io::loadPCDFile("E:\\File\\gradPaper\\data\\station\\3Clip.pcd", *target);
	//pcl::io::loadPCDFile("E:\\File\\gradPaper\\data\\station\\4Clip.pcd", *source);
	pcl::io::loadPCDFile("E:\\File\\gradPaper\\data\\cube1.pcd", *target);
	pcl::io::loadPCDFile("E:\\File\\gradPaper\\data\\cube2.pcd", *source);

	Eigen::Vector4f pcaCentroidtarget;//容量为4的列向量
	pcl::compute3DCentroid(*target, pcaCentroidtarget);//计算目标点云质心
	Eigen::Matrix3f covariance;//创建一个3行3列的矩阵，里面每个元素均为float类型
	pcl::computeCovarianceMatrixNormalized(*target, pcaCentroidtarget, covariance);//计算目标点云协方差矩阵
	Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance, Eigen::ComputeEigenvectors);//构造一个计算特定矩阵的类对象
	Eigen::Matrix3f eigenVectorsPCA = eigen_solver.eigenvectors();//eigenvectors计算特征向量
	//Eigen::Vector3f eigenValuesPCA = eigen_solver.eigenvalues();//eigenvalues计算特征值

	Eigen::Vector4f pcaCentroidsource;
	pcl::compute3DCentroid(*source, pcaCentroidsource);//计算源点云质心
	Eigen::Matrix3f model_covariance;
	pcl::computeCovarianceMatrixNormalized(*source, pcaCentroidsource, model_covariance);//计算源点云协方差矩阵
	Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> modeleigen_solver(model_covariance, Eigen::ComputeEigenvectors);
	Eigen::Matrix3f model_eigenVectorsPCA = modeleigen_solver.eigenvectors();
	//Eigen::Vector3f model_eigenValuesPCA = modeleigen_solver.eigenvalues();

	pcl::PointCloud<pcl::PointXYZ>::Ptr target_t(new pcl::PointCloud<pcl::PointXYZ>);
	//平移目标点云，将目标点云通过质心平移到原点
	Eigen::Matrix4f translation_t = Eigen::Matrix4f::Identity();
	//设置矩阵的元素
	translation_t(0, 3) = -pcaCentroidtarget[0];
	translation_t(1, 3) = -pcaCentroidtarget[1];
	translation_t(2, 3) = -pcaCentroidtarget[2];
	pcl::transformPointCloud(*target, *target_t, translation_t);

	pcl::PointCloud<pcl::PointXYZ>::Ptr source_t(new pcl::PointCloud<pcl::PointXYZ>);
	//平移源点云，将源点云通过质心平移到原点
	Eigen::Matrix4f translation_s = Eigen::Matrix4f::Identity();
	//设置矩阵的元素
	translation_s(0, 3) = -pcaCentroidsource[0];
	translation_s(1, 3) = -pcaCentroidsource[1];
	translation_s(2, 3) = -pcaCentroidsource[2];
	pcl::transformPointCloud(*source, *source_t, translation_s);

	// 计算旋转
	Eigen::Vector3f n0;
	double angle0;
	calRotation(eigenVectorsPCA.col(2), model_eigenVectorsPCA.col(2), angle0, n0); // 假设最大特征值在最后一列
	Eigen::Matrix4f transform0 = RodriguesMatrixTranslation(n0, angle0);

	// 应用旋转
	pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_source(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::transformPointCloud(*source_t, *transformed_source, transform0);

	// 输出旋转矩阵
	std::cout << "Rotation Matrix:" << std::endl;
	std::cout << transform0 << std::endl;

	// 可视化
	pcl::visualization::PCLVisualizer viewer("PCLVisualizer");
	viewer.initCameraParameters();

	int v1(0);
	viewer.createViewPort(0.0, 0.0, 0.5, 1.0, v1);
	viewer.setBackgroundColor(128.0 / 255.0, 138.0 / 255.0, 135.0 / 255.0, v1);
	viewer.addText("Cloud before transforming", 10, 10, "v1 test", v1);
	pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> color_v1(target, 0, 255, 0);
	viewer.addPointCloud<pcl::PointXYZ>(target, color_v1, "color_v1", v1);
	viewer.addPointCloud<pcl::PointXYZ>(source, "source", v1);
	viewer.addCoordinateSystem(0.5, "v1 test", v1);

	int v2(0);
	viewer.createViewPort(0.5, 0.0, 1.0, 1.0, v2);
	viewer.setBackgroundColor(128.0 / 255.0, 138.0 / 255.0, 135.0 / 255.0, v2);
	viewer.addText("Cloud after transforming", 10, 10, "v2 test", v2);
	pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> color_v2(target_t, 0, 255, 0);
	viewer.addPointCloud<pcl::PointXYZ>(target_t, color_v2, "color_v2", v2);
	viewer.addPointCloud<pcl::PointXYZ>(transformed_source, "transformed_source", v2);
	viewer.addCoordinateSystem(0.5, "v2 test", v2);

	while (!viewer.wasStopped())
	{
		viewer.spinOnce(100);
	}
	return 0;
}

// 计算向量u与向量v之间的夹角
void calRotation(Eigen::Vector3f u, Eigen::Vector3f v, double& angle, Eigen::Vector3f& vec)
{
	angle = acos(u.dot(v) / (u.norm() * v.norm()));
	if (angle > M_PI / 2)
	{
		u = -u;
		angle = M_PI - angle;
	}
	float i, j, k;
	i = u(1) * v(2) - u(2) * v(1), j = v(0) * u(2) - v(2) * u(0), k = u(0) * v(1) - u(1) * v(0);
	vec << i, j, k;
	double value = sqrt(i * i + j * j + k * k);
	vec(0) = vec(0) / value;
	vec(1) = vec(1) / value;
	vec(2) = vec(2) / value;
}

//获取罗德里格斯旋转矩阵
Eigen::Matrix4f RodriguesMatrixTranslation(Eigen::Vector3f n, double angle)
{
	//罗德里格斯公式求旋转矩阵
	Eigen::Matrix4f x_transform(Eigen::Matrix4f::Identity());
	x_transform(0, 0) = cos(angle) + n(0) * n(0) * (1 - cos(angle));
	x_transform(1, 0) = n(2) * sin(angle) + n(0) * n(1) * (1 - cos(angle));
	x_transform(2, 0) = -n(1) * sin(angle) + n(0) * n(2) * (1 - cos(angle));
	x_transform(0, 1) = n(0) * n(1) * (1 - cos(angle)) - n(2) * sin(angle);
	x_transform(1, 1) = cos(angle) + n(1) * n(1) * (1 - cos(angle));
	x_transform(2, 1) = n(0) * sin(angle) + n(1) * n(2) * (1 - cos(angle));
	x_transform(0, 2) = n(1) * sin(angle) + n(0) * n(2) * (1 - cos(angle));
	x_transform(1, 2) = -n(0) * sin(angle) + n(1) * n(2) * (1 - cos(angle));
	x_transform(2, 2) = cos(angle) + n(2) * n(2) * (1 - cos(angle));

	return  x_transform;
}

最大主成分对齐效果：

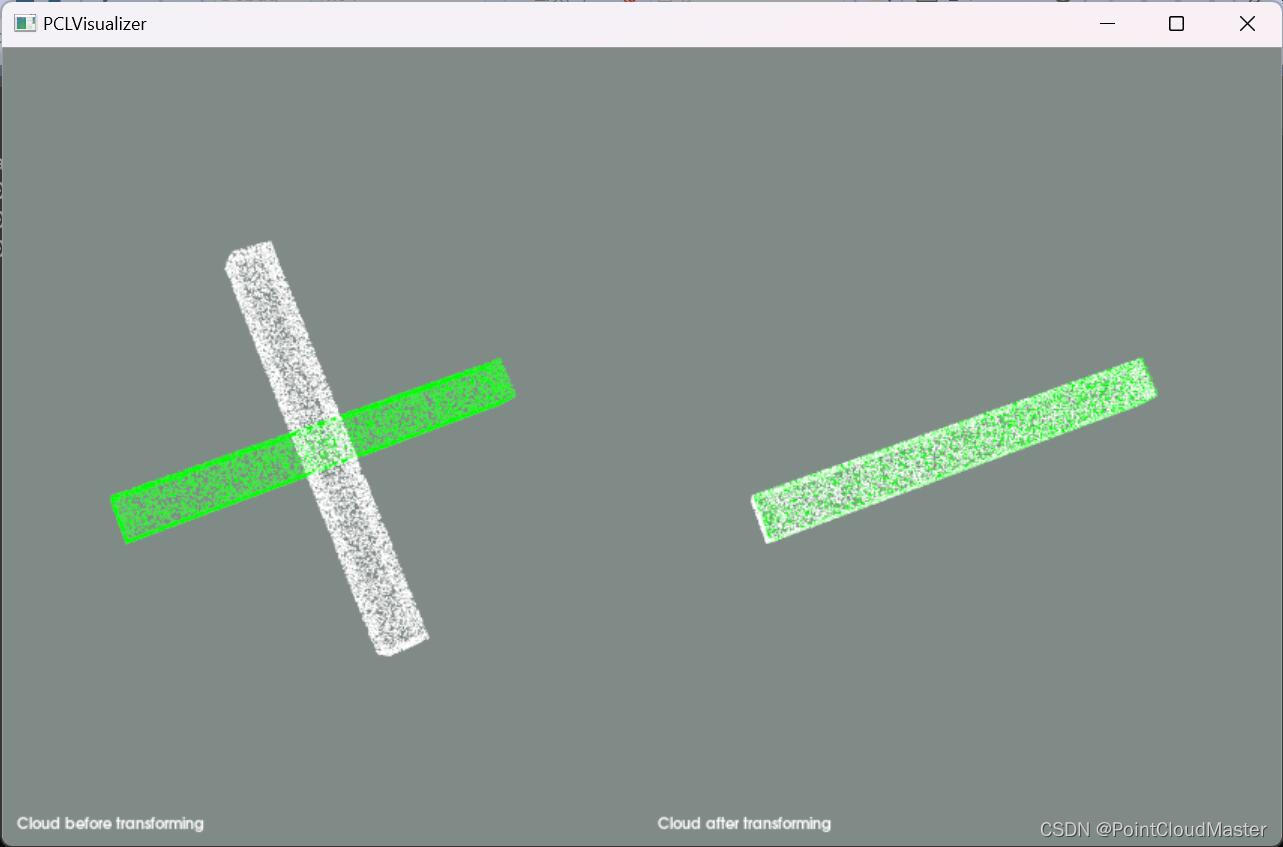
结论：

PCA在点云配准中的应用提供了一种有效的方法来处理和分析具有明显几何结构的点云。通过识别和对齐点云的主要特征，PCA可以实现快速且准确的配准，尤其适用于结构化且噪声水平适中的点云数据。

PCA 实现点云粗配准（python版本）【2025最新版】
点云侠的博客
04-03 29万+
python版本的主成分分析（PCA）实现点云粗配准。博客长期更新，本文最近一次更新时间为：2025年2月11日
PCA 点云配准
点云兔子的博客
07-20 1181
PCA计算变换矩阵用时72.322s变换矩阵为效果不咋地，一看就是陷入局部最优了。PCA计算变换矩阵用时51.573s变换矩阵为httpsR%5EdhttpshttpshttpsR%5Erhttpshttpsv_%7Bi%7Dhttpsu_%7Bi%7Dhttpshttpshttpshttpshttpshttps。
PCL点云库——PCA粗配准
fei_12138的博客
07-12 8158
PCA配准 　　主成分分析法( Principal Component Analysis，简称PCA)是使数据简化的算法，通过揭露数据内部的主要分布方向，减少了数据集的维数，从而保留了点云集中贡献最大的特征，更好地解释数据的变化规律。PCA 算法进行点云配准是以主方向为依据，根据两点云的主方向计算出对应的三个旋转和三个平移量，可大致对齐两点云数据。 　　 #include <pcl/visualization/cloud_viewer.h> #include <pcl/io/pcd_io.
点云处理系列 - 点云配准
最新发布
Adunn的专栏
02-12 2239
1. 点云配准 点云配准是将两个或多个点云数据集融合到一个统一的坐标系统中的过程。这通常是为了创建一个完整的模型或融合从不同视角采集的数据。 点云配准一般分为粗配准和精配准，粗配准指的是在两幅点云之间的变换完全未知的情况下进行较为粗糙的配准，目的主要是为精配准提供较好的变换初值；精配准则是给定一个初始变换，进一步优化得到更精确的变换。 2. 点云粗配准: 特征匹配、穷举搜索、概率分布 3. 点云精配准：基于优化（ICP、GICP、NICP、图优化、GMM、半定规划）、特征学习、端到端学习
PCL点云处理之基于PCA的点云配准（一百一十四）
weixin_44329757的博客
03-18 1020
这里实现一种基于PCA的点云配准方法，在两片点云的位置和方向都相差较大情况下，进行配准。
基于PCA的点云位姿估计与粗拼接，matlab实现
04-04
使用主元分析法PCA对两片点云数据作粗略的拼接配准，可以作为ICP算法的预处理步骤。尝试规定了PCA主元向量的朝向。附带ply文件格式的bunny多视角数据。
Open3D 点云配准-PCA算法配准（粗配准）
纵马踏花向自由
07-10 774
PCA（Principal Component Analysis，主成分分析）是一种用于降维和特征提取的统计方法。在点云处理中，PCA可以用于点云配准（alignment），即通过对齐两个点云的主成分轴来进行粗略的配准。
点云配准(CloudCompare软件)
热门推荐
dayuhaitang1的博客
03-05 2万+
话不多说，直奔正题。 文章目录一、Align配准算法二、ICP配准算法 一、Align配准算法 1.打开软件，加载数据。 2、为了便于我们分辨，修改数据的颜色。 同上过程，将配准2数据修改为绿色。 3、同时选择配准1和配准2数据，然后再选择配准Align配准方法进行配准。 4、选择自己要配准的数据，另一个数据则会成为参考数据。 5、选择对应的特征点，这个按自己的需求，不过至少需要3对特征点...
ISS 点云关键点检测算法数学推导
cicy5219的博客
11-28 1031
是一种关键点检测算法，基于点云局部几何特性提取显著点。这些关键点对点云描述具有较高稳定性和抗噪性，常用于三维配准、匹配等任务。Threshold21Threshold21​（主方向和次主方向的变异比值）反映了局部点云是否接近于一条直线（低比值）或一个平面（高比值）。低比值通常表示局部数据点接近于直线或曲线（非常狭窄的分布），高比值则表示数据点主要分布在平面上。
常用3D点云数据免费下载
11-16
3. **点云配准**：通过匹配算法，将多个视角或时间点的点云数据对齐，形成一个统一的三维模型。常用的配准方法有ICP（Iterative Closest Point）及其变种。 4. **点云拟合**：利用数学方法（如最小二乘法）找出点云...
案例研究深度解析：ERDAS土地覆盖校正实战技巧
![案例研究深度解析：ERDAS土地覆盖校正实战技巧]...文章深入分析了土地覆盖分类与解译的理论与方法，并提供了分类操作的实践经验及分类结果的评估与优化策略。接着，详细阐述了土地覆盖变化检测技术的原理、工
pca变换实现3D图像刚性配准的初配准
03-06
用PCA实现3D刚性图像配准的初配准，模拟了3D的长方体数据，对其进行旋转和平移，然后通过提取主方向，根据两个数据体的主方向计算出应有的三个旋转和三个平移量。
【点云分类与滤波的艺术】：结合分类信息进行精准滤波的高级技术
![【点云分类与滤波的艺术】：结合分类信息进行精准滤波的高级技术]... # 摘要 点云数据处理是三维空间信息获取与分析中的关键环节，对于目标分类、物体识别及环境重建等领域具有重要意义。本文首先介绍了点云数据处理...
【点云融合入门到精通】：13个技巧，带你从新手到专家
# 摘要 点云融合作为一种技术手段，对于从多源数据中提取高质量的3D模型信息至关重要。本文首先介绍了点云融合的基本概念及其...点云配准；3D建模；自动驾驶 参考资源链接：[点云多帧融合实践：RGB点云融合实验解析](h
基于PCL的PCA算法实现点云的粗配准
HackWhisper的博客
08-17 651
本文将介绍如何使用PCL库中的PCA算法实现点云的粗配准，并提供相应的源代码。本文介绍了如何利用PCL库中的PCA算法实现点云的粗配准，并提供了相应的源代码。通过计算点云数据的协方差矩阵和特征向量，我们可以找到最佳的旋转矩阵，实现点云的对齐和配准。PCA算法通过计算数据的协方差矩阵，找到数据中的主成分方向，从而实现数据的降维和特征提取。在点云粗配准中，我们可以利用PCA算法来寻找点云数据的主轴方向，进而找到最佳的旋转矩阵。根据输入的源点云和目标点云，程序将输出配准后的结果，并显示配准误差。
点云粗配准算法的实现：主成分分析（PCA）
EvktJava的博客
09-26 525
这是一个简单的点云粗配准示例，使用主成分分析（PCA）算法来提取特征并计算旋转矩阵。然而，点云配准是一个复杂的问题，实际应用中可能需要更多的步骤和算法来实现更准确的配准。点云配准是计算机视觉和三维几何处理中的重要任务，它的目标是将多个点云数据集对齐，使它们在空间中尽可能接近。本文将介绍如何使用主成分分析（PCA）算法实现点云的粗配准。通过提取特征、计算旋转矩阵和应用旋转矩阵，我们可以将两个点云数据集进行粗略的对齐。请注意，这只是一个简单的示例，实际应用中可能需要更复杂的算法和步骤来实现更准确的配准。
三维点云处理-PCA主成分分析
weixin_49401384的博客
04-18 2193
三维点云处理在三维重建、SLAM、机器人感知等领域都有涉及，那么如何更好地分析和利用三维点云数据也一直是一个比较热门的研究话题。常用的三维点云处理库如 PCL（Point Cloud Library）和 Open3D等。点云通常是指某个坐标系下点的集合。每个点可以包含多个维度的信息，如空间三维坐标（XYZ）、颜色（RGB）、强度值（Intensity）等等。
用PCA实现点云配准——Python教程
带你成为别人眼中的大佬！
04-01 1001
用PCA实现点云配准——Python教程点云粗配准是计算机视觉领域中常用的技术之一。在许多工业应用场景中，我们需要合并不同传感器获取的带有噪声和偏差的点云数据，获得高精度的三维模型。这时点云粗配准就可以发挥作用了！本教程将使用Python编写实现点云配准的代码，并利用PCA（主成分分析）算法对点云进行粗略的配准。
基于PCA的点云配准与粗拼接附Matlab代码
CyberSparkZ的博客
08-09 311
在很多应用中，我们需要将不同位置、姿态、光照下的点云进行配准，以得到更完整、准确的三维场景重建结果。点云配准的任务是将两个或多个不同位置、姿态、光照下的点云对齐，使它们具有相同的参考坐标系，从而实现点云的精确匹配。该方法可以通过计算点云的协方差矩阵和特征向量分解来估计两个点云之间的位姿关系，从而实现点云的配准和粗略拼接。在点云配准中，我们可以利用PCA方法来估计两个点云之间的位姿关系。需要注意的是，如果要展示两个点云的对齐情况，需要将它们放在同一个坐标系中，通常需要手动调整视角和坐标轴。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Qt, C++

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值