【线性代数】矩阵的算数运算

西瓜WiFi

已于 2022-06-14 20:20:35 修改

阅读量2.7k

点赞数

分类专栏： Pandas 文章标签：矩阵线性代数 python

于 2022-06-13 00:00:10 首次发布

本文链接：https://blog.csdn.net/m0_62011685/article/details/125252113

版权

Pandas 专栏收录该内容

20 篇文章

订阅专栏

一、线性方程组和矩阵

设有n个未知数m个方程的线性方程组：
在这里插入图片描述

二、矩阵的数学定义

在这里插入图片描述

三、矩阵的算数运算

3.1矩阵的加减法
大小相同的矩阵（同型矩阵）才可以进行矩阵的加减运算，同型矩阵之间的加减运算，是把对应位置元素相加减。

3.2矩阵的乘法
在这里插入图片描述

使用Numpy解题：

A=np.mat([[4,-1,2,1],[1,1,0,3],[0,3,1,4]])
B=np.mat([[1,2],[0,1],[3,0],[-1,2]])
print(A*B)

在这里插入图片描述

使用Numpy计算：

A=np.mat([[-2,4],[1,-2]])
B=np.mat([[2,4],[-3,-6]])
print('矩阵AB的乘积')
print(A*B)
print('='*50)
print('矩阵BA的乘积')
print(B*A)

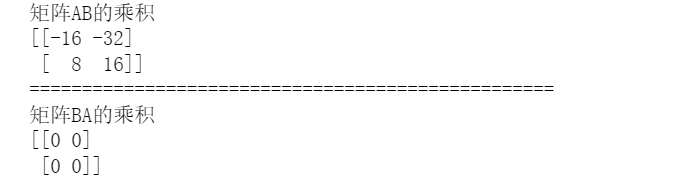
在这里插入图片描述

四、矩阵的幂运算

在这里插入图片描述

五、矩阵乘法的应用

有两张表销售表和产品表如下所示，计算每家终端的总价和产品的总质量。
销售表：

产品表：

import pandas as pd 
import numpy as np
sal=pd.DataFrame({
    '终端':['A','B','C'],
    '产品1':[12,213,246],
    '产品2':[23,24,546],
    '产品3':[54,65,54],
    '产品4':[23,89,25]
})
product=pd.DataFrame({
    '产品':['产品1','产品2','产品3','产品4'],
    '单价':[100,99,88,46],
    '单件质量':[10,15,20,30]
})
#矩阵相乘计算总价和总质量
df=pd.DataFrame(np.mat(sal.iloc[:,1:].values)*np.mat(product.iloc[:,1:].values),columns=['总价','总质量'])
sal_final=pd.concat([sal,df],axis=1)
sal_final