模式识别——统计决策方法——最小风险贝叶斯决策

模式识别——统计决策方法——最小风险贝叶斯决策

前言

​ 现在再回到猜硬币的那个简单的例子上来。前面给出的是在最小错误率的原则下得到
的决策规则，但是，根据具体的场合不同，我们应关心的有可能并不仅仅是错误率，而是错误所带来的损失：毕竞，把一角误认为是五角与把五角误认为是一角所带来的损失是不同的。
​ 同样，在癌细胞识别的例子中，我们不但应该关心所作的决策是否错误，更应该关心决
策错误所带来的损失惑风险。比如，如果把正常细胞误判为癌细胞，会给病人带来精神上的负担和不必要的进一步检查，这是一种损失；反之，如果把癌细胞误判为正常细胞，则损失更大，因为这可能会导致病人丧失了宝费的早期发现癌症的机会，可能会造成影响病人生命的严重后果。将这两种类型的错误一视同仁来对待，在很多情况下是不恰当的。

最小风险贝叶斯决策

已知条件

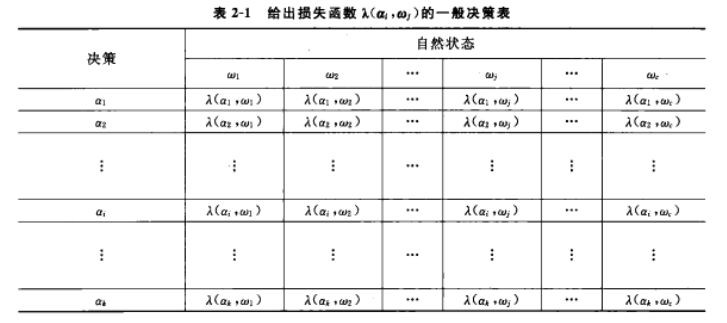
（1）损失函数决策表

​ 设对于实际状态为w的向量x，采取决策α所带来的损失为
$$\lambda ({\alpha }_i,w_j),i=\mathrm{1...}k,j=\mathrm{1...}c$$
（假定有c个类别，每个类别决策有k种，注意k可以不等于c，因为我们可以做出拒绝的决策，即无法判断属于任何一类）

称作损失函数。通常它可以用表格的形式给出，叫做决策表，如表2-1所示。在应用中需要根据题的背景知识确定合理的决策表。

（2）类条件概率密度/似然度

（3）前验概率

决策规则

对于某个样本x，它属于各个状态的后验概率是$P(w_j|x,j=\mathrm{1...}c)$，对它采取决策${\alpha }_i,i=\mathrm{1...}k$的期望损失是
$$R({\alpha }_i|x)=E[\lambda ({\alpha }_i,w_j)|x]=\sum _{j=1}^c\lambda ({\alpha }_i,w_j)P(w_j|x)$$
相当于对决策表的某一行从左往右的值乘上对应后验概率求和

对所有可能的样本，期望损失是
$$R(\alpha )=\int R(\alpha (x)|x)p(x)dx$$
最小风险贝叶斯决策就是最小化这一期望风险
$$minR(\alpha )$$
其中对于后验概率的算法与最小错误率贝叶斯决策中使用的贝叶斯公式一致

计算过程

贝叶斯公式计算后验概率

$$P(w_j|x)=\frac{p(x|w_j)P(w_j)}{P(x)}=\frac{p(x|w_j)P(w_j)}{{\sum }_{j=1}^{c}p(x|w_j)P(w_j)}$$

计算决策风险

$$R({\alpha }_i|x)=\sum _{j=1}^c\lambda ({\alpha }_i,w_j)P(w_j|x)$$

选择风险最小的决策

$$\alpha =argmi{n}_{i}R({\alpha }_i)$$

课本例题

已知条件为
$$\begin{array}{rl}& P(w_1)=0.9,P(w_2)=0.1\\ & p(x|w_1)=0.2,p(x|w_w)=0.4\\ & {\lambda }_{11}=0,{\lambda }_{12}=6\\ & {\lambda }_{21}=1,{\lambda }_{22}=0\end{array}$$
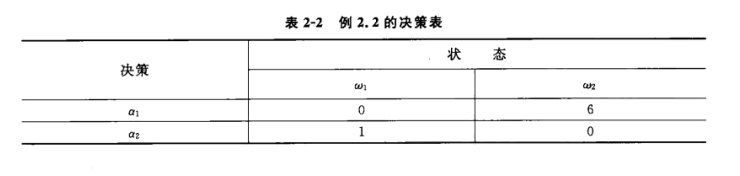
利用表2-2的决策表，按最小风险贝叶斯决策进行分类。

由贝叶斯公式计算得
$$P(w_1|x)=0.818,P(w_2|x)=0.182$$
结合决策表计算决策风险为
$$\begin{gathered} R({\alpha }_1|x)={\lambda }_{11}P(w_1|x)+{\lambda }_{12}P(w_2|x)=1.092 \\ R({\alpha }_2|x)={\lambda }_{21}P(w_1|x)+{\lambda }_{22}P(w_2|x)=0.818 \end{gathered}$$
因为$R({\alpha }_1|x)>R({\alpha }_2|x)$，决策为$w_2的风险小于w_1$

分类为$w_2$

与最小错误率贝叶斯决策的区别

最小风险贝叶斯决策更加适用于我们生活中的各种情况，而最小错误率贝叶斯决策是最小风险贝叶斯决策的特例，以二分类为例，最小错误率贝叶斯决策对应着${\lambda }_{11}={\lambda }_{22}=0,{\lambda }_{12}={\lambda }_{21}=1$的情况

策是最小风险贝叶斯决策的特例，以二分类为例，最小错误率贝叶斯决策对应着${\lambda }_{11}={\lambda }_{22}=0,{\lambda }_{12}={\lambda }_{21}=1$的情况